(1) 군집분석이란?
- 비지도학습 중 하나
- 여러 변수로 표현된 자료들 사이의 유사성을 측정하고 유사한 자료들끼리 몇 개의 군지으로 묶고 다변량 분석을 활용하여 각 군집에 대한 특징을 파악하는 기법
- 관측치의 유사성 측정하기 위한 거리측도 : 유클라디안거리, 맨하튼 거리 등
- 유사성 측도 : 코사인 거리, 상관계수
- 거리가 가까울 수록 유사성이 큼
- 평가지표 : 실루엣 계수 -> 응집도와 분리도 계산, 1에 가까울 수록 완벽하기 분리되었다 판단.
(2) 거리척도
- 연속형 변수
- 유클라디안 거리 (Euclidean)
- 두 점 사이 거리 계산할 때 가장 널리 쓰이는 계산 방법, 가장 짧은 거리 계산
- 통계적 개념이 포함되지 않은 수학적 거리, 변수들의 산포 정도를 감안 x
- 맨하튼 거리 (Manhattan)
- 두 점 사이를 가로지르지 않고 길을 따라 갔을 때 거리, 수학적 거리, 시가거리
- 변수들 차이의 단순합으로 계산한 거리
- 체비셰프 거리 (Chebychev)
변수 간 거리 차이 중 최댓값을 데이터 간의 거리로 정의
변수들 차이의 단순합으로 계산한 거리 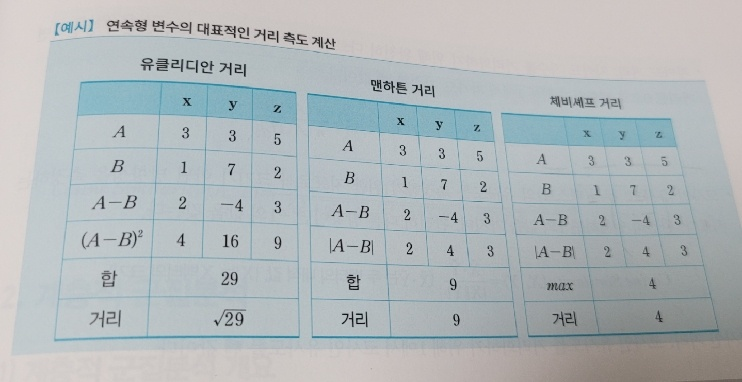
- 범주형 변수
- 얼마나 많은 공통된 요소를 갖고 있는지 판단할 수 있다.
- 단순 일치 계수 (SMC)
- 두 객체 i와 j 간의 상이성을 불일치 비율로 계산
- 자카드 지수
- 두 집합 사이의 유사도를 측정하는 지표, 두 집합이 같으면 1, 완전히 다르면 0의 값을 가짐
- 자카드 거리
- 자카드 지수를 거리화하기 위해 완전히 다르면 먼 거리를 갖는 1, 완전히 동일하면 거리를 0으로 변환하기 위함
- 1 - 자카드지수
- 코사인 유사도
- 문서(텍스트)의 유사도를 측정하기 위한 지표, 크기가 아닌 방향성을 측정하는 지표
- 완전히 일치하면 1의 값, 완전히 다른 방향이면 -1의 값
- 코사인 거리
- 코사인 유사도를 거리화하기 위해 1 - 코사인 유사도
- 순위 상관 계수
- 순서척도인 두 데이터 사이 거리 측정하기 위한 지표
- 스피어만 상관계수를 사용할 수 있다.


(3) 계층적 군집 분석
- 개별 관측치 간의 거리를 계산해서 가장 가까운 관측치부터 결합해나가면서 계층적 트리 구조를 형성, 이를 통해 군집화를 수행하는 방법
- 병합적 방법 - 각 데이터를 하나의 군집으로 간주, 가까운 데이터부터 순차적으로 병합하는 방법
- 분할적 방법 - 전체 데이터를 하나의 군집으로 간주하고 각각의 관측치가 하나의 군집이 될 때까지 (종료조건까지) 군집을 순차적으로 분할하는 방법
- 군집 간 거리
- 관측 벡터 간의 거리뿐만 아니라 군집 간 거리에 대한 정의 필요
- 단일 (single)연결법 (최단연결법)
- 생성된 군집과 기존의 데이터들의 거리를 가장 가까운 데이토로 계산하는 방법
- 대부분 관측치가 멀리 떨어져 있어도 하나의 관측치만 다른 군집과 가까이 있으면 병합 가능
- 완전연결법 (최장연결법, complete)
- 생성된 군집과 기존의 데이터들의 거리를 가장 먼 데이터로 계산하는 방법
- 내부 응집성에 중점을 둔 방법, 둥근 형태 군집 형성
- 평균연결법
- 생성된 군집과 기존 데이터들의 거리를 군집 내 평균 데이터로 계산하는 방법
- 계산량이 불필요하게 많아질 수 있으며, 단일.완전 연결법보다 이상치에 덜 민감
- 중심연결법
- 각 군집 중심점 사이 거리를 거리로 정의
- 평균 연결법 보다 계산량이 적고, 모든 관측치 사이의 거리를 측정할 필요 없이 중심 사이 거리 한 번만 계산
- 와드연결법
- 생성된 군집과 기존의 데이터들의 거리를 군집 내 오차가 최소가 되는 데이터로 계산하는 방법
- 비슷한 크기의 군집끼리 병합하는 경향이 있음, 군집 내 분산을 최소로 하기 때문에 좀 더 조밀한 군집이 생성 가능
(4) 비계층적 군집 분석
- 구하고자 하는 군집의 수를 사전에 정의해 정해진 군집의 수만큼 형성하는 방법
- 데이터 간 거리행렬을 사용하여 분석을 수행 x
- 원하는 군집의 수(k)의 초깃값을 설정하고 분석을 수행
- 대표적인 방법으로 k-means(k-평균) 군집이 있다.
- K-means 군집
- 군집의 수(k개)를 사전에 정한 뒤, 집단 내 동질성과 집단 간 이질성이 모두 높에 전체 데이터를 k개의 군집으로 분할하는 알고리즘
- k 값을 정하기 위해 <- 제곱합 그래프 이용
- 군집의 수 k의 초깃값을 설정하고 각각 k를 설명할 변수의 값을 임의로 설정하거나 데이터 중에서 k개를 선택 (seed)
- 장점 : 분석 기법 적용이 단순하고 빠름, 다양한 데이터에서 사용가능
- 단점 : 초깃값 k개 설정이 어려움, 결과 해석 어려움, 연속형 변수여야 함, 안정된 군집 보장 but 최적 보장 x, 이상값에 민감
- DBSCAN
- 밀도 기반 군집분석의 한 방법, 개체들이 밀접한 정도에 기초해 군집 형성
- 데이터 분포가 기하학적, 노이즈가 포함된 데이터셋에 대해서도 효과적으로 군집 형성 가능, 초기 군집의 수를 설정 필요 x
(5) 혼합 분포 군집 사용 (Mixture of Normal Distribution)
- 모형 기반의 군집 방법
- 같은 확률 분포에서 추출된 데이터들끼리 군집화하는 분석 기법
- EM 알고리즘 (기댓값 최대화) -> 확률 모델의 최대 가능도를 갖는 모수와 함께 그 확률 모델의 가중치를 추정하고자 함
(6) 자기조직화지도(SOM, 코호넨 맵)
- 인공신경망 기반 차원축소와 군집을 동시에 수행할 수 있는 알고리즘
- 고차원 데이터를 한눈에 파악하기 쉬운 저차원(2차원) 공간에 정렬하여 나타내는 시각화 방법 중 하나
- 인공신경망 일종이지만 은닉층 보유 x, 순전파 방식만 사용하여 알고리즘 수행속도 매우 빠름
- 장점 : 순전파 방식을 사용 -> 속도 매우 빠름, 저차원 지도 시각적 이해 쉬움, 패턴 발견 및 이미지 분석에 성능 우수, 입력 데이터 속성 그대로 보존
- 단점 : 초기 학습률 및 초기 가중치에 많은 영향 받음. 경쟁층 이상적인 노드 수 결정 어려움
(7) 군집 모형 평가
- 외부 평가 - 자카드 계수, 분류모형 평가 방법 응용
- 내부 평가 - 단순 계산법, 군집 간거리 계산, 엘보메소드
- 실루엣 계수 -> 하나의 데이터와 나머지 모든 데이터와의 거리 활용 -> 지금 데이터가 속한 군집 안에 데이터들이 잘 속해 있는지 평가하는 방법
- -1부터 1까지 범위 가짐, 1에 가까울 수록 -> 군집 매우 잘됨, 1인경우 군집보다 모든 데이터가 정확하게 분류되었다고 얘기할 수 있는 수준



