Complexity-복잡도에 대해
복잡도란 알고리즘의 효율성을 분석하기 위한 개념이다. 복잡도는 시간 복잡도와 공간 복잡도로 나뉘는데, 시간 복잡도는 알고리즘의 연산 횟수에 중점을 두고 공간 복잡도는 알고리즘이 차지하는 메모리와 관련있다. 최근에는 메모리 성능이 늘어남에 따라 공간 복잡도보다 시간 복잡도에 더 중점을 두고 알고리즘을 짠다고 한다.
점근표기법과 big-O 표기법
점근표기법은 간단하게 가장 큰 항만을 생각하고 이 외의 항이나 상수항 등을 생략하여 표기하는 방법이다.
간단한 예를 들어 f(n) = n^2 + n + 1이라는 함수가 있을 때, n = 1이라면 n^2가 차지하는 비율은 전체의 33%정도일 뿐이다. 그러나 n이 커질수록 n^2가 차지하는 비율은 늘어나며 가장 높은 차수의 항만 남겨도 될 만큼 영향력이 커진다.
이에 기반한 big-O표기법의 정의는 다음과 같다.
두 개의 함수 f(n), g(n)이 주어졌을 때, 모든 n > n_0에 대해 |f(n)| ≤ c|g(n)|을 만족하는 상수 c, n_0이 있다면 f(n) = O(g(n))이다.
f(n) = n^2 + n + 1의 Big-O 표기는 O(n^2)이다.
가장 높은 차수의 항이 차지하는 비율 그래프. n이 10만 되어도 n^2가 90%를 차지한다.
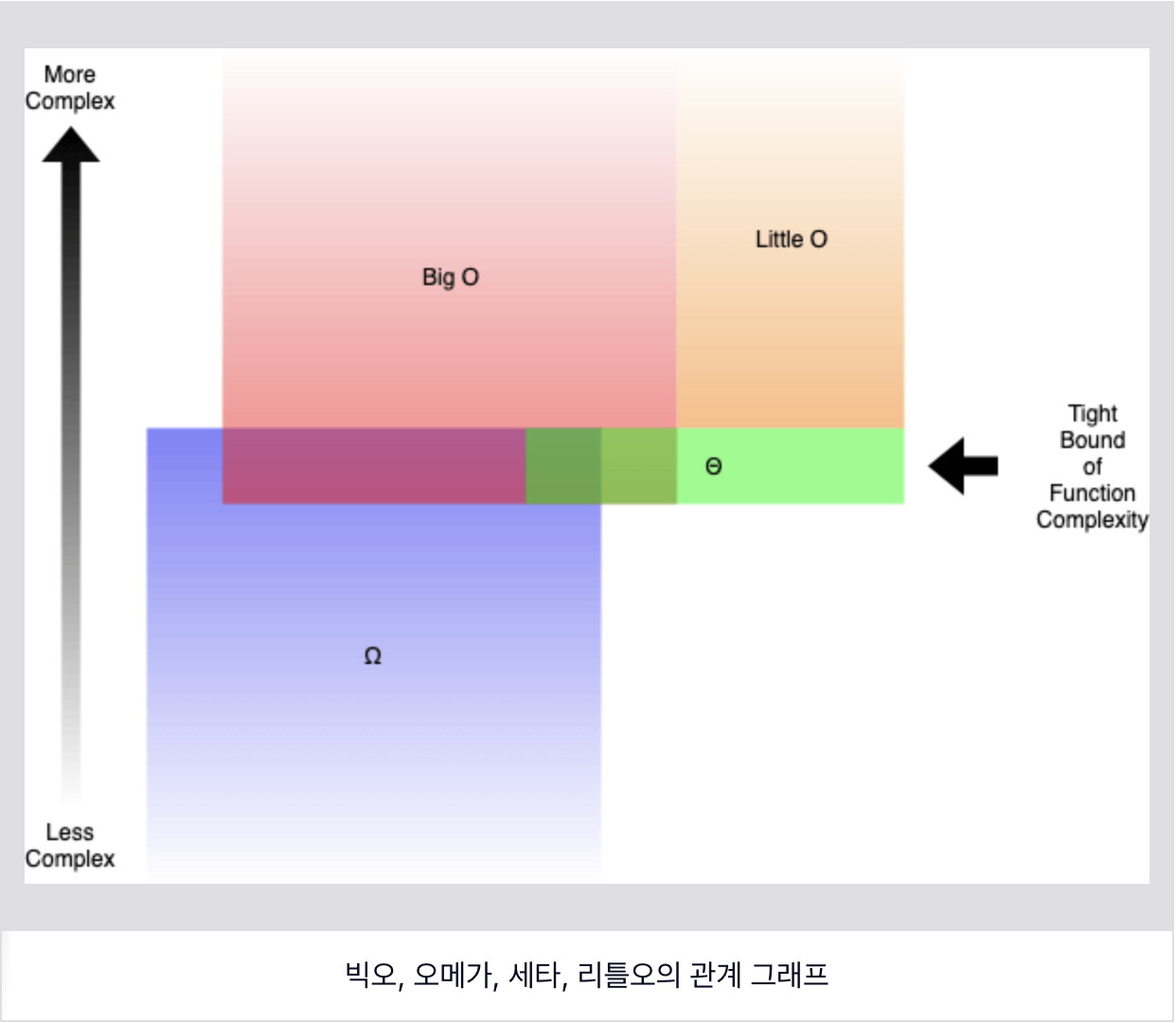
여러 case에서의 표기법
알고리즘을 표기하는 점근적표기법은 big-O 표기법 외에도 big-θ, big-Ω, little-o가 있다.
big-O는 위쪽 범위를 나타낸다.
big-Ω는 아래쪽 범위를 나타낸다.
big-θ는 평균적인 또는 정확한 범위를 나타낸다.
little-o는 복잡도의 정확한 범위를 제외한 위쪽을 나타낸다.
이중 big-O가 가장 자주 사용되는 이유는 알고리즘이 복잡할 수록 big-θ를 구하기 어렵고 상한에 가까운 효율로 실행될 여지는 적기 때문이다.
다시 big-O 표기법으로 표시하는 함수들은 복잡도가 얼마나 빠르게 증가하느냐에 다음과 같이 비교할 수 있다.
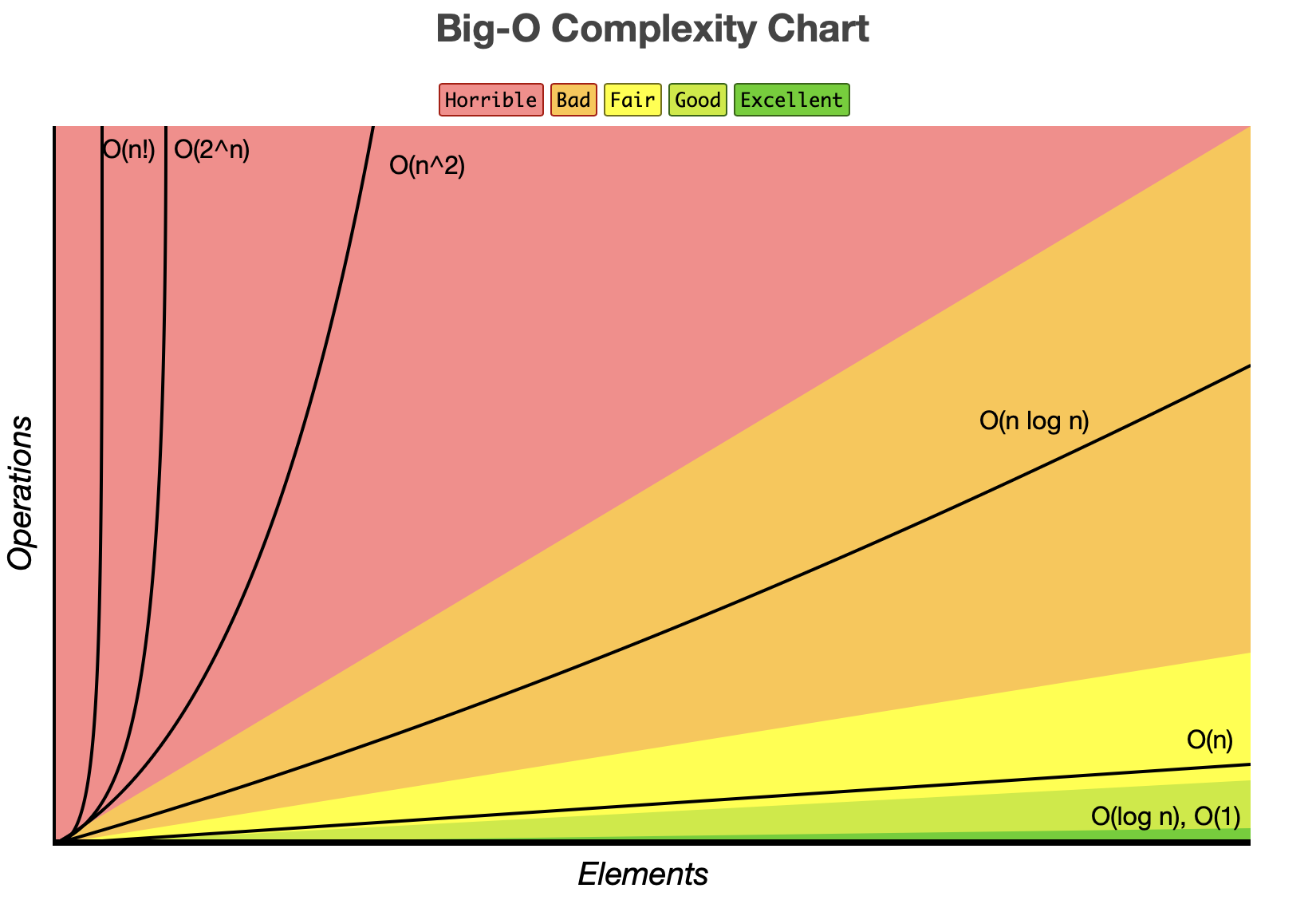
O(1) < O(logN) < O(N) < O(NlogN ) < O(N^2) < O(2^N) < O(N!)
점근적 접근 보단 step 수를 세는 것이 훨씬 정확하고 실무에선 2배, 3배 등도 영향력이 있다. 다만 복잡도가 높은 알고리즘은 n이 커진다면 언젠가는 복잡도가 낮은 알고리즘을 역전한다는 것을 알 수 있고 구분이 가능하다는 점에서 의미 있다고 한다.
예시 문제와 코드 그리고 스위프트에서의 적용
문제
어떤 이미지가 2D 배열의 픽셀로 표현되어 있다. 만약 중첩 for문을 사용해서 모든 픽셀들을 반복하게 된다면 (그 뜻은 바깥의 for문이 모든 열-column-을 따라 반복할 때에
안에 있는 for문은 모든 행-row-을 따라 반복한다는 것이다.) 여기에서 이미지가 함수의 입력값(input)이라면 이 함수의 시간 복잡도는 무엇일까?
정답
O(n)
중첩 for문이라 O(n^2)으로 생각하기 쉽지만 N을 따질 땐 입력값을 기준으로 생각해야 하며 입력값인 image의 픽셀은 한 번씩만 입력되므로 O(n)이 답이 된다.
코드에서 알아보기
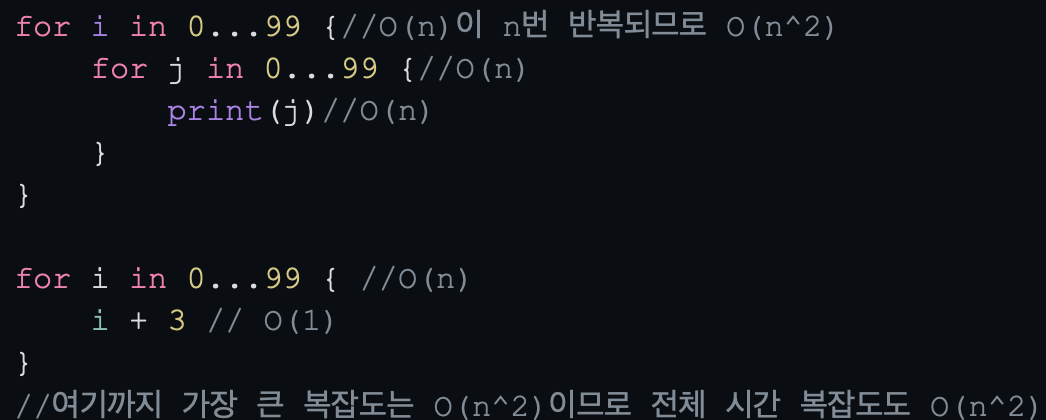
for i in 0...99 {//O(n)이 n번 반복되므로 O(n^2)
for j in 0...99 {//O(n)
print(j)//O(1)
}
}
for i in 0...99 { //O(n)
i + 3 // O(1)
}
//여기까지 가장 큰 복잡도는 O(n^2)이므로 전체 시간 복잡도도 O(n^2)스위프트에서의 적용
스위프트 메서드에 대한 시간 복잡도를 레퍼런스까지 함께 정리해두신 블로그이다.
스위프트를 어느정도 익힌 뒤에 다시 읽어보면 더 도움이 될 거 같다.
아래의 탐색 예시를 보니 적절한 메소드나 알고리즘을 고르는 게 어떤 느낌인지 와닿았다.
if word.count == 0 // O(n)
if word.isEmpty // O(1)
출처
https://www.freecodecamp.org/korean/news/big-o-notation-why-it-matters-and-why-it-doesnt-1674cfa8a23c/
https://www.freecodecamp.org
https://blog.naver.com/kisooofficial/223249892915
