캡스톤 디자인 프로젝트

김봉석·2021년 9월 25일

Supply Chain Optimization using reinoforcement learning

주제 : stochastic, seasonal, demand 상황하에서 Supply Chain Cost 최적화

서론

1) 강화학습의 의미, 딥러닝의 의미

강화 학습은 기본적으로 시행 착오를 통해 학습하는 자율적 인자가 학습 시스템. 보상 최적화를 목표로 작업을 수행하는 것임. 즉, 최상의 결과를 얻기 위해 수행함으로써 학습하는 것임. 딥 러닝은 기본적으로 기존 데이터를 사용하여 패턴을 찾기 위해 계산을 훈련 한 다음, 이를 사용하여 새로운 정보에 대한 예측을 만드는 주권적인자가 학습 방법임. 이들의 차이점은 딥 러닝은 훈련 그룹에서 학습 한 다음 해당 학습을 새로운 데이터 장소에 적용하는 반면 강화 학습은 보상을 최적화하기 위해 지속적인 피드백을 기반으로 활동을 조정하여 동적으로 학습한다는 것.

2) 백과사전에서의 최적화 vs 강화학습

최적화의 연구는 최적해의 존재와 특성에 초점을 맞춘다는 점에서 학습과 근사의 측면에서 접근하는 강화 학습과 다름
 즉, 최적해가 존재하고 그것을 찾는 것이 최적화라면 강화학습은 최적해가 없지만 학습을 통해 최적에 근사한 값을 찾아나가는 점에 차이점이 있음

3) 공급망의 재고관리에 대해 강화학습으로 연구하는 이유

지금까지 공급망의 재고관리에 관한 대부분의 연구는 고객 수요가 통계적 분포를 통해 미리 알려져 있으며, 안정적인(stationary) 수요를 갖는 비교적 단순한 공급망 네트워크를 대상으로 확률적 모델이나 해석적 모델 등을 활용하는 수리적인 접근 방법을 통해 최적해 또는 근사 최적해를 도출하고자 하였다. 이러한 기존의 공급망 관련 연구 방법들은 비교적 정확한 결과값을 제시하지만, 노드의 수가 늘어나거나 다른 제약조건이 추가될 경우 수치적으로 접근하기에 한계가 있어 비교적 제한된 범위에 적용될 수밖에 없으며 그 결과를 실제 문제에 적용하기에 많은 어려움이 따르는 한계점이 존재
$\rightarrow$ 한계점을 극복하고 보다 실제적인 공급망에 적용 가능한 재고정책을 위해 불확실한 고객 수요가 발생하는 공급망을 대상으로 하는 적응형 재고정책을 제안 & 강화학습(reinforcement learning) 기법을 적용하는데, 행동-보상 학습이란 에이전트의 시행착오(trial-and-error)를 이용한 인공 지능형 학습 방법으로써 주어진 환경 하에서 가장 높은 보상을 얻을 수 있는 행동이 다음 계획기간에 선택될 확률이 높아지도록 학습함으로써, 고객 수요의 변화에 대처하여 최적의 행동이 선택될 수 있도록 지원하는 것임.

4) Stochastic seasonal demand

참고 논문 : Reinforcement learning for supply chain optimization

재고관리 시스템에서 확률적 모형

확정적 모형과 달리 확률적 모형에서는 수요에 변동이 있다고 가정함
수요의 변동이 적은 경우 수요에 대한 예측이 상대적으로 쉽고 불확실성이 낮은 반면, 수요의 변동이 큰 경우 수요예측에서 오류가 발생할 가능성이 크고 불확실성도 커지게 됨
수요에 대한 불확실성이 큰 경우 예측에 기반하여 확보한 재고에 비해 수요가 초과하여 품절현상이 나타 나게 될 위험에 대비하여 안전재고를 보유하게 됨
이 모형에서도 확정적 모형에서 사용하는 가정을 주로 사용하나, 수요의 경우에는 확률적으로 파악 가능 하지만 시간에 따라 일정하지 않고 변동을 한다고 가정함
확률적 모형에서도 주문량은 EOQ를 사용하게 됨. 다만 연간수요가 시간에 따라 균일하지 않으므로 연간 평균수요(D)를 사용하게 됨.
재주문점을 정하는 데 있어서 확정적 모형과의 차이가 나타나게 되는데 확정적 모형에서는 리드타임 동안의 평균 수요만을 반영하여 재주문점을 결정하였으나 확률적 모형에서는 리드타임 동안의 평균 수요와 안전재고(ss: safety stock)를 포함하여 결정하게 됨

5) 강화학습을 사용하는 이유

관련 자료를 찾아봤을때, 강화학습을 적용하는것이 유의미한 이유는 다음과 같습니다.

1) 최적화하는 대상의 수가 많아 질수록 , 제약사항이 많을 수록 기존 optimization 방법은 한계가 있습니다.

2) 불확실한 고객 수요가 발생하는 공급망을 대상으로 하는 적응형 재고정책을 제안할 수 있습니다.

4) 기존의 확률적 EOQ 방식은 수요가 시간에 따라 바뀌는 특성을 고려하지 않고, 평균 수요를 고려하여 사용됩니다.
강화학습의 경우 시간을 고려하는 방식이기 때문에 시간에 따라 적합한 판단을 할 수있습니다.

Question) demand를 어떻게 구성할 것인가?

Stochastic seasonal demand를 어떻게 발생시킬 것인가에 대해서 몇가지 자료를 참고해 보았으나
제대로 이해하기 힘들었습니다.

이해한 바로는, 어떤 주기성을 가진 함수 (예를 들어 sin, cos 함수) + random noise (예를 들어, $U(0,1)$ or $N(0,1)$ 를 더해서 발생시키는 것 같은데 어떻게 구성 해야할지 자세히 모르겠습니다..

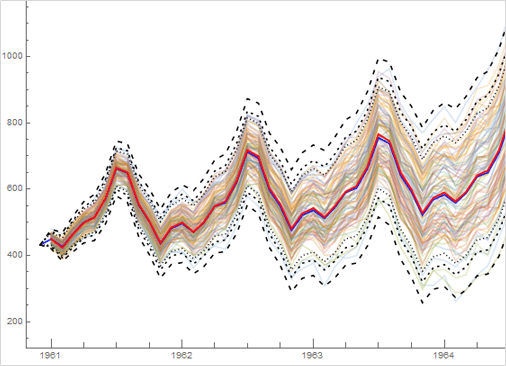
밑의 그림은 위의 참고한 논문에서 가정한 demand 입니다.
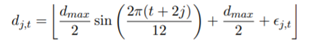
demand example

본론

구성할 suply chain 예시

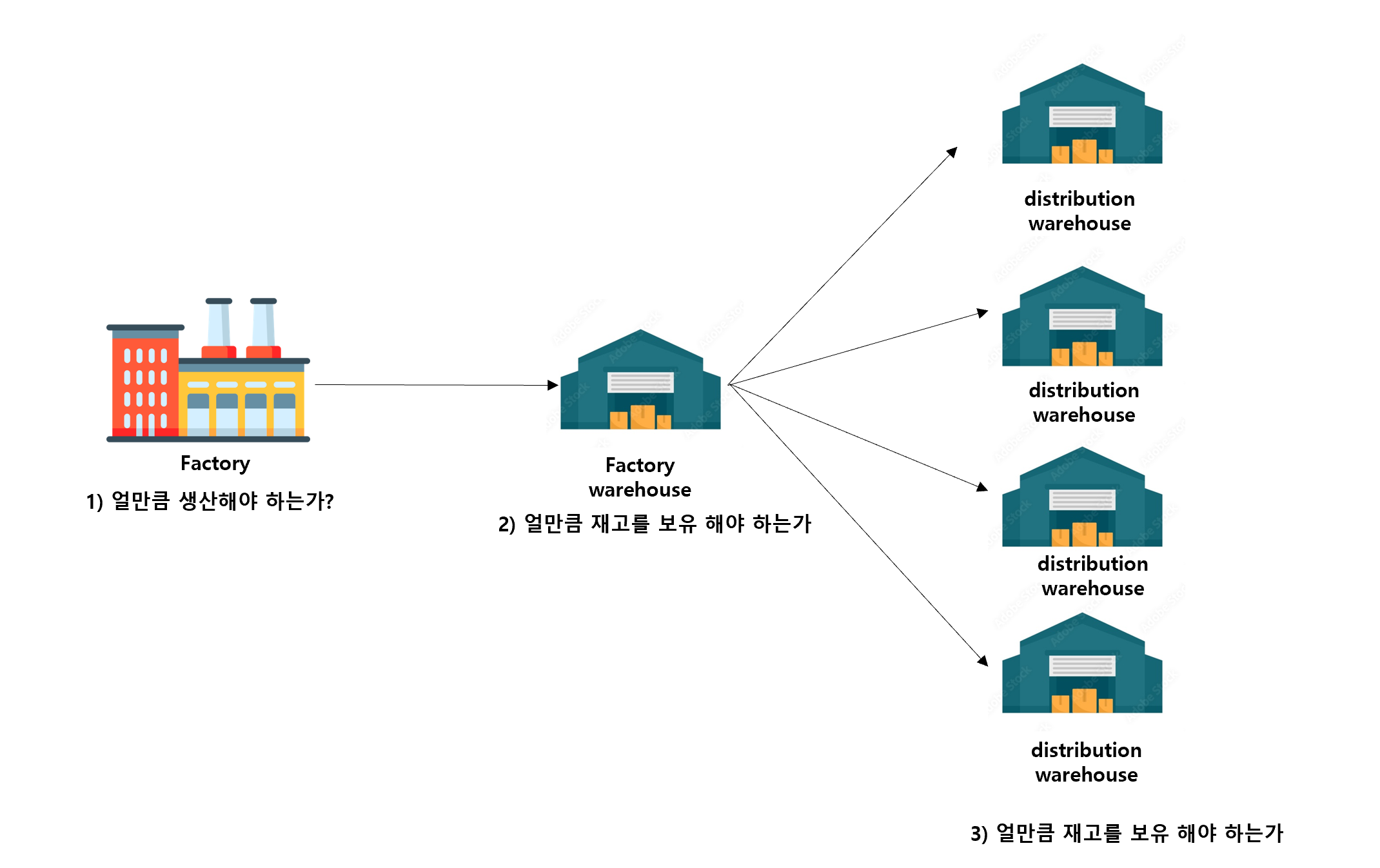
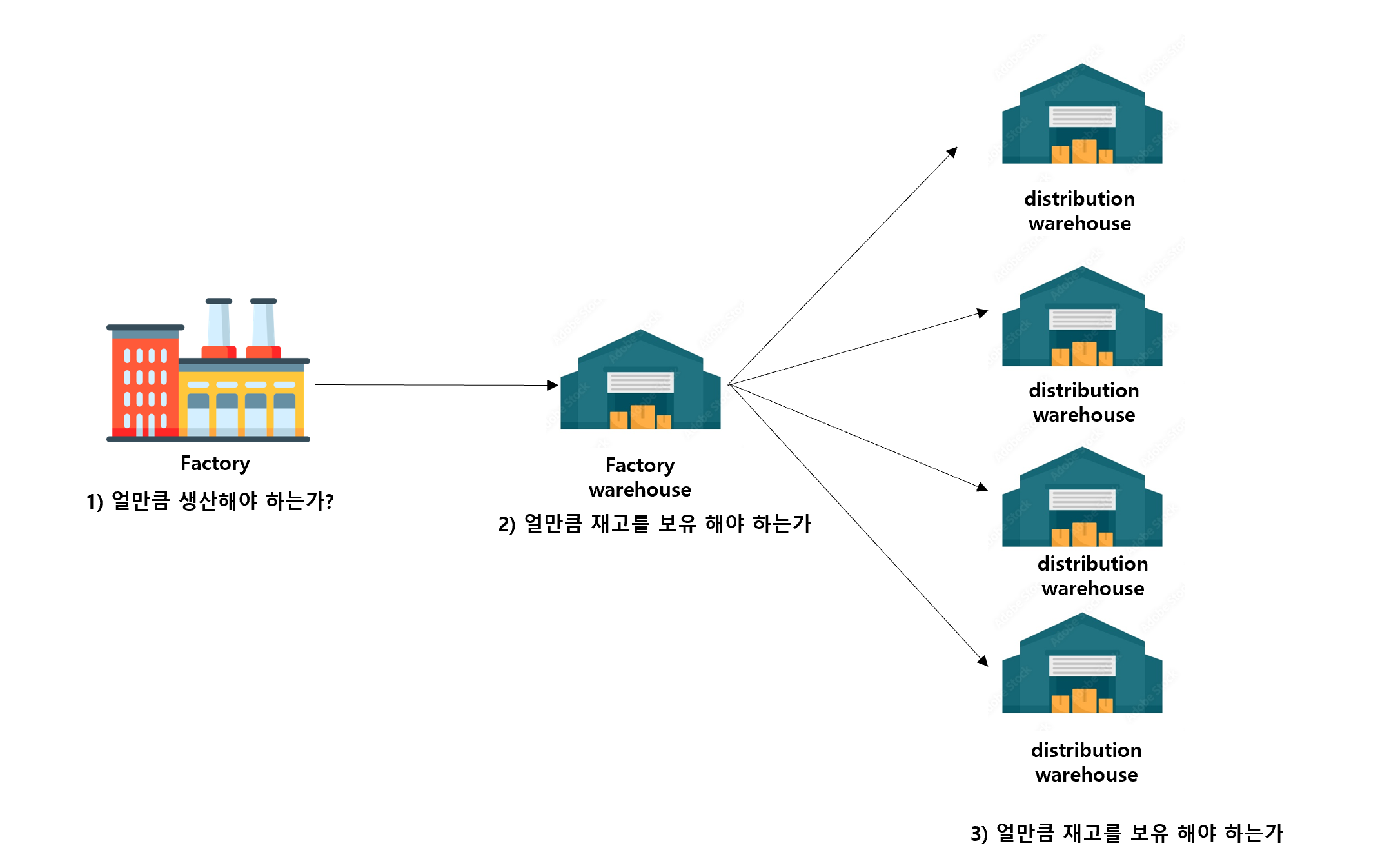
구성할 Supply chain은 다음과 같은 형태를 가집니다.
하나의 공장과 공장 창고가 있고, 여러개의 분배 창고가 있는 형태입니다.

해결 해야할 문제

Objective : Supply chain의 Profit을 Maximize

Agent가 결정해야할 action은 다음과 같습니다.
1) factory : 얼마만큼 생산해야 하는가?
2) factory warehouse & distribution warehouse : 얼마만큼 공장 창고에서, 분배창고로 보내야 하는가?

위의 1,2 결정에 의해 각 창고의 재고 수준이 변화하게 되고, 그에 따라 Stochastic & Seasonal demand를 충족 시킬 수 있을 수도 없을 수도 있습니다.

이러한 상황 속에서 Supply chain 전체 profit을 Maximize 하는 action을 학습시키는것이 프로젝트의 목표입니다.

3. MDP formulation

참고 자료 : Deep reinforcement learning for supply chain and price optimization 포스트

참고 자료 : github

참고 자료 : How to Improve your Supply Chain with Deep Reinforcement Learning 포스트

참고 자료 : 시뮬레이션 최적화 방법을 이용한 다단계 공급망 재고 관리

용어 정의

$f$ : factory
$fw$ : factory warehouse
$w_j$ : distribution warehouse j

ex) $sc_{fw}$ : storage cost at factory warehouse

factory 부분 :

notation	내용	설명
$a_{f,t}$	production level at time $t$	공장에서 얼만큼 생산 해야 하는가?
$pc_{f}$	production cost per unit	생산단가는 얼마인가? (constant 고정 이라 가정)

factory warehouse 부분 :

notation	내용	설명
$a_{w_j,t}$	number of products shipped to warehouse $w_j$ at time t $t$	factorty warehouse 에서 warehouse j로 얼만큼 보내야하는가?
$sc_{fw}$	storage cost at factory warehouse	factory warehouse 재고 유지비용은 얼마인가? (constant 고정 이라 가정)
$c_{fw}$	maximum capacity of factory warehouse	공장 창고의 최대 수용 용량은 얼마인가
$q_{fw,t}$	stock level at time $t$	현재 시점 $t$ 에서 공장 창고 재고 수준은 얼마인가?

distribution warehouse 부분

notation	내용	설명
$bc_{w_j}$	back order cost at warehouse j	분배 창고 $w_j$ 의 backorder cost 얼마인가? (constant 고정 이라 가정)
$tc_{w_j}$	transportation cost per unit for warehouse j	factory wharehouse 에서 distribution wahrehouse j 까지 수송 비용은 얼마인가?
$c_{w_j}$	maximum capacity of factory warehouse	분배 창고 j의 최대 수용 용량은 얼마인가
$q_{w_j,t}$	current capacity of factory warehouse at time $t$	현재 시점 $t$ 에서 분배 창고 재고 수준은 얼마인가?
$d_{w_j,t}$	demand at warehouse j at time $t$	현재 시점 $t$ 에서 분배 창고 j의 수요는 얼마인가?
$p$	product price for retailer	소매업자 에게 판매되는 제품 가격은 얼마인가?
$sc_{w_j}$	storage cost at warehouse j	분배창고의 재고 유지비용은 얼마인가?

가정

공장(factory)에서는 개당 원가가 $pc_f$ 달러의 제품을 생산한다.
$t$ 시점에서 공장의 생산 수준은 is $a_{f,t}$ 이다.
공장의 창고와, 분배 창고에는 최대 용량 수준이 있으며 재고 비용이 발생한다.
- fatory warehouse $\rightarrow$ 최대 용량 : $c_{fw}$ , 재고수준 : $q_{fw,t}$ , 재고 비용: $sc_{fw}$
- distribution- warehouse $\rightarrow$ 최대용량: $c_{w_j}$ , 재고수준 : $q_{w_j,t}$ 재고비용 $sc_{w_j}$
$t$ 시점에서, 공장창고로 부터 분배 창고 $j$ 까지 옮기는 출하량은 $a_{w_j,t}$ 이며 운송 비용 $tc_{w_j}$ 가 발생한다.
제품은 모든 분배 창고에서 동일한 가격 $p$ 로 소매업자에게 판매된다.
- $t$ 시점에서 분배 창고 $j$ 에 발생한 수요는 $d_{j,t}$ 이다.
- 수요는 Stochastic, Seasonal 성을 가진것으로 가정한다.
- 만약 수요를 충족시키지 못 할시 단위 당 back order cost, $bc_{w_j}$ 가 발생한다.

1. State

$S_t = (q_{fw,t}, q_{w_1,t} ... q_{w_j,t}, d_{t-1}, \cdots d_{t-\tau}$ ) where, $d_t = [d_{w_1,t},d_{w_2,t},...d_{w_j,t}]$

$q_{fw,t}, q_{w_1,t} ... q_{w_j,t}$ : 현재 시점 $t$ 에서, 공장의 창고와 분배 창고의 재고 수준은 얼마나 되는가?
$[d_{t-1}, \cdots d_{t-\tau}]$ : 과거의 수요 패턴, $t-1$ 점부터 $t-\tau$ 까지의 수요는 어떠 했는가?
* $d_t = [d_{w_1,t},d_{w_2,t},...d_{w_j,t}]$ : 시점 $t$ 에서, 모든 분배 창고의 각 수요는 얼마나 되는가?

State는 현재 시점의 모든 창고(공장, 분배 창고)의 재고 수준과, 이전 시점 $t-1$ 부터 $t-\tau$ 까지의 모든 창고의 수요량으로 구성됩니다. Agent는 현재 시점과 미래의 demand를 관측하지 못하고, 과거의 수요 패턴만 관찰 할 수 있습니다. 이는 Agent가 스스로 과거의 패턴들을 학습하고. 수요 예측 기능을 포함 시키는 policy을 학습시키기 위함 입니다.

의견 : 만약 Agent가 학습이 잘된다면 문제가 없지만, 그렇지 못할경우
LSTM을 통하여 따로 수요예측 모델을 만들고 예측 값을 Agent에 주는 방법도 가능한 방법이라 생각합니다.

2. Action

Agent가 결정할 action은 크게 두가지 종류입니다.

1) $a_{f,t}$ : $t$ 시점에서 공장에서 얼만큼 생산 해야하는가?
2) $a_{w_j,t}$ : $t$ 시점에서 공장 창고에서 분배 창고 $j$ 로 얼만큼 보내야 하는가?

$\therefore$ $a_t$ = [ $a_{f,t},a_{w_1,t} \cdots,a_{w_j,t}$ ]

의견 : 연구의 차별성을 위해 Continous Action space를 가지는 경우를 시도해보고 싶으나, 결정해야할 action의 개수가 유통창고가 n개일때, 1+n 개이므로 1+n개의 continous action space는 힘들 수도 있습니다.안될경우 disrete Action space또한 염두해 두고 있습니다.

3. Transition

remind $S_t = (q_{fw,t}, q_{w_1,t} ... q_{w_j,t}, d_{t-1}, \cdots d_{t-\tau}$ )

state transition 다음과 같은 rule을 따릅니다.

$S_{t+1}$ =
$[min(q_{fw,t}+a_{f,t} -\sum_{j=1}^W a_{w_j,t}, c_{fw})$ , (factory warehouse stock update)
$min(q_{w_1,t} +a_{w_1,t} -d_{w_1,t}, c_{w_j})$ , $\cdots$ , $min(q_{w_j,t} +a_{w_j,t} -d_{w_j,t}, c_{w_j})$ ] (distribution warehouse update)
$d_t \cdots, d_{t-\tau}$ ] (demand update)

설명)

$min(q_{fw,t}+a_{f,t} -\sum_{j=1}^W a_{w_j,t}, c_{fw})$
- min(현재 공장 창고 재고 수준 + 생산량 - 분배창고에 보낸수송량, 공창 창고의 최대 수용량)
- 이 부분에서 허점이 있습니다. 공장 창고에서, 현재 수용량 보다 공장에서 많은 양을 생산해서 받은 경우 최대 수용량 까지 받고 나머지는 사라지게 됩니다.

$min(q_{w_1,t} +a_{w_1,t} -d_{w_1,t}, c_{w_j})$ , $\cdots$ , $min(q_{w_j,t} +a_{w_j,t} -d_{w_j,t}, c_{w_j})$ ]
- min(분배 창고의 재고수준 + 수송해서 받은 량 + 수요 충족량, 분배 창고의 최대 수용량)
- 마찬가지로. 분배 창고에서, 현재 수용량 보다 창고 공장에서 많이 받은 경우 최대 수용량 까지 받고 나머지는 사라지게 됩니다.
$d_t \cdots, d_{t-\tau}$ , Sliding window 방식과 유사

4. Reward

리워드는 다음과 같이 Supply chain의 profit 관점에서 5개의 텀으로 이루어집니다.

revenue : $p\sum_{j=1}^n d_{w_j,t}$
- product price for retailer $\cdot$ demand for each warehouse j at time $t$ )

production cost : $pc_f \cdot a_{f,t}$
- production cost per unit $\cdot$ production level at time $t$

storage cost : $sc_{fw} \cdot max(q_{fw,t},0)+\sum_{j=1}^n sc_{w_j} \cdot max(q_{w_j,t},0)$
- (factory warehouse storage cost $\cdot$ factory warehouse stock level at time $t$ ) + (distribution warehouse storage cost $\cdot$ distribution warehouse stock level at time $t$ )
transportation cost : $\sum_{j=1}^n tc_{w_j} \cdot a_{w_j,t}$
- transprotation cost $\cdot$ number of product shipped to warehouse j at time $t$
backorder cost : $\sum_{j=1}^n bc_{w_j} \cdot min(q_{w_j},0)$ =
- backorder cost $\cdot$ Unfulfilled demand at time 4t$
- Note: assume that negative product level unfulfilled demand
- 허점 : demand를 만족시키지 못할 경우, backorder cost만 내고 해당 하는 demand는 사라짐
  현실에서는, cost도 발생함과 동시에 늦게라도 demand를 만족시켜야 함
  - 이 가정을 추가한다면, 강화학습을 사용하는게 더 유의미해 지지 않을까 생각합니다. 만약 지금 즉시 demand를 만족 시키는 것보다 코스트를 내서라도 delayed 해서 만족시키는게 더 이익인 경우를 고려 할 수 있습니다.

$\therefore r_t$ = [ $p\sum_{j=1}^n d_{w_j,t}$ ] - [ $pc_f \cdot a_{f,t}$ ] -[ $sc_{fw} \cdot max(q_{fw,t},0)+\sum_{j=1}^n sc_{w_j} \cdot max(q_{w_j,t},0)$ ] - [ $\sum_{j=1}^n tc_{w_j} \cdot a_{w_j,t}$ ] + [ $\sum_{j=1}^n bc_{w_j} \cdot min(q_{w_j},0)$ ]

reward(net income) = revenue -production cost - storage cost - transportation cost + backorder cost

4. 해결해야 할 사항

MDP 구성에 있어서의 허점
- 위의 MDP 형태를 보면 허점이 많이 존재합니다.

참고한 github에는 RLlib라는 Scikit-learn과 같은 이미 만들어진 library를 사용하고 있습니다.
- RLlib은 사용해본적이 없고, 자유도가 떨어집니다.
- 피드백을 받은후, 직접 pytorch를 이용해서 Agent 코드를 작성할 예정입니다.

Stocastic & seasnal demand를 어떻게 만들어 내는가?
- 이부분에 대한 지식이 전혀 없어 어려움을 겪고 있습니다.
- 일단 참고자료의 형태를 적용할 계획입니다.
Extension
- 지금까지 작성한 글로 프로젝트를 진행한다면, 참고자료의 글들을 코드로 구현한 것에 불과 하지 않다는 생각이 드는 것 같습니다
- 뭔가 더 extension이 필요하지 않나 생각합니다

LP

매시점마다 LP를 풀어서 비교해 보자.

해결해야할 사항 : 원래 환경 구성 min,max 있어서 비선형 식임
이것을 선형제약조건으로 다 바꿔서 풀어야함.

demand : 매시점 평균 수요 사용
ex) (2019년 1월, 2020년 1월, 2021년 1월) 평균

현재 : demand 만드는 법 -> sin 식( 매시점 결정 되있음 )+ random 요소 (Unifrom 분포)

np.round(self.demand_max/2 + self.demand_max/2*np.sin(2*np.pi*(time_step + 2)/self.time_length*2) + np.random.randint(0, self.demand_var))

self.demand_max = 상수 고정
self.time_length = 상수 고정
time_step = t시점마다 바뀌지만 t시점 마다 풀거니깐 알 고 있음.

평균 수요 = 따라서 sin 식에서 random의 평균만 구해서 더하면 됨

decision variable

x : 얼마나 생산할 것인가
y : 얼마나 공장창고에서 분배 창고로 보낼것인가

주어지는거 상수 :
self.factory_wh_cap = 40 (고정)
self.dt_wh_cap =20 ,(고정)
self.unit_price = 100 (고정)
self.unit_cost = 40 (고정)
self.storage_cost = 2 (고정)
self.transportation_cost=5 (고정)

self.factory_wh_stock = 0 (매시점 바뀌지만 알고있음), a라 하자.
self.dt_wh_stock = 0 , (매시점 바뀌지만 알고있음), b라 하자
Demand = 뭐 c 이라 하자

공장에서 물건을 생산해서, 공장창고로 보낸다.
production cost : x * 20 (생산량 * unit_cost)
- 제약조건 1 : 공장창고의 용량을 넘길 수 없다. (a+x) <= 40, 공장창고의 capaicty 40보다 a+x가 작아야된다
공장창고에서 저장 비용 발생한다
factory storage cost : (a+x)2 (현재 재고량 + 생산량)저장비용 = 재고비용
공장창고에서 분배 창고로 보낸다.
transportation cost : 5y ( 운송비용 보낸는 량) 인데, 공장창고 현재 재고량 보다 많이 보낼수 없다
- 제약 조건 2: 현재 factory 재고 용량 보다 많은량을 보낼 수 없다. y <= a+x
분배 창고에서 받았다. 분배 창고 용량을 넘어서면 안된다.
- 제약조건 3 : b+y <= 20 (분배 창고 원래 재고 + 받은량<=분배창고 용량)
분배 창고 storage cost, 발생 : (b+y)*2
revenue /penalty cost 계산 (막힌 부분)
- 파이썬을 통한 환경 구성에서 if-else로 상황을 나눠서 했는데, 제약 조건식으로 어떻게 해야하는가?

if b+y>=c, 현재 분배 창고 재고 >= demand

-> 충분히 재고가 demand를 만족하고 남는다.
demand량 만큼 revenue가 발생하고, pnelaty cost는 없다.
revenue : c*100 (demand * unit price)
penaly cost : 0

else b+y<=c, 현재 분배 창고 재고 <demand:
-> 현재 창고의 재고는 demand를 전부 만족시키지 못한다
현재 분배 창고에 있는 모든 재고를 소진해서, revenue 발생하고
나머지 용량망큼 패널티 코스트가 발생한다..
revenue : (b+y)*100 (현재 재고량 * unit price)
penalty cost : (c-(b+y))*100 (만족 시키지 못한량 * penalty cost )

Objective

profit
x40 + (a+x)2 + 5*y +revenue + penlaty cost (if-else문 처리를 만족시키는 방법들을 찾아야함)

constraint

1.0<=x <= 20 (공장 창고 생산량 제약 걍 정하면됨)
2. (a+x) <= 20
3. b+y <= 40
4. 0<=y<=a+x
5. revnue /penlaty cost if-else 처리 constraint (해야될것)

푸는법

매 t 시점마다 , 위의 현재 환경의, 상수 정보를 받아와서
파이썬 pulp를 사용해서 푼다.

quesetion

1) 공장 - 공장창고 - 분배창고
인데도 LP로 문제를 formulation 하기 힘든데

창고를 3~4개로 늘리면 식을 세워서 풀 수 있을까?

김봉석

이전 포스트

[Python] argparse 사용법

다음 포스트