알고리즘이란
- 어떤 목적을 달성하거나 결과물을 만들어내기 위해 거쳐야 하는 일련의 과정들
- 여러가지 상황에 따른 알고리즘은 모두 다르다. 따라서 시간 복잡도가 가장 낮은 알고리즘을 선택하여 사용한다.
시간복잡도
알고리즘이 문제를 해결하기 위한 시간(연산)의 횟수를 말한다.
알고리즘을 평가하는데 있어 수행시관과 메모리 사용량을 평가기준으로 두는데
수행시간에 해당하는 것이 시간 복잡도(Time Complexity)
메모리 사용량에 해당하는 것이 공간 복잡도(Space Complexity)
- 시간 복잡도를 이용하면 작성한 코드가 대략 얼마나 걸릴지 예상할 수 있다.
- 표기법으로 대문자 O를 사용한다. (다양한 시간 복잡도가 많지만, 보통 Big-O만 사용한다.)
Big O 표기법
Big O가 중요한 이유를 알기 위해서는 Asymptotic Complexity에 대해 알야아한다.알고리즘의 성능평가는 시간복잡도와 공간복잡도를 계산하고, 적 표기법으로 나타내면 된다.
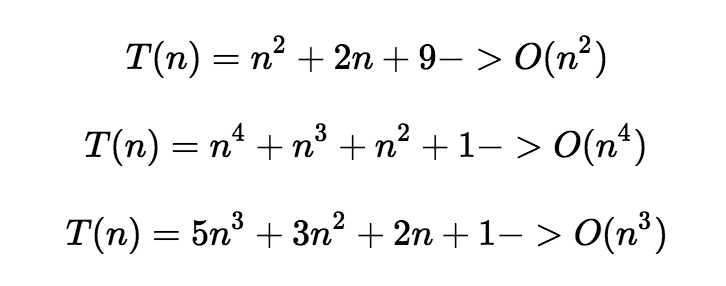
위 예와 같이 T(n)으로 표현한 함수의 최고차항의 차수가 빅오가 된다.빅오의 순서는 아래와 같고 커질수록 좋지 않다. 보통 O(n^2)이상의 복잡도를 가지는 알고리즘은 좋지 않다.
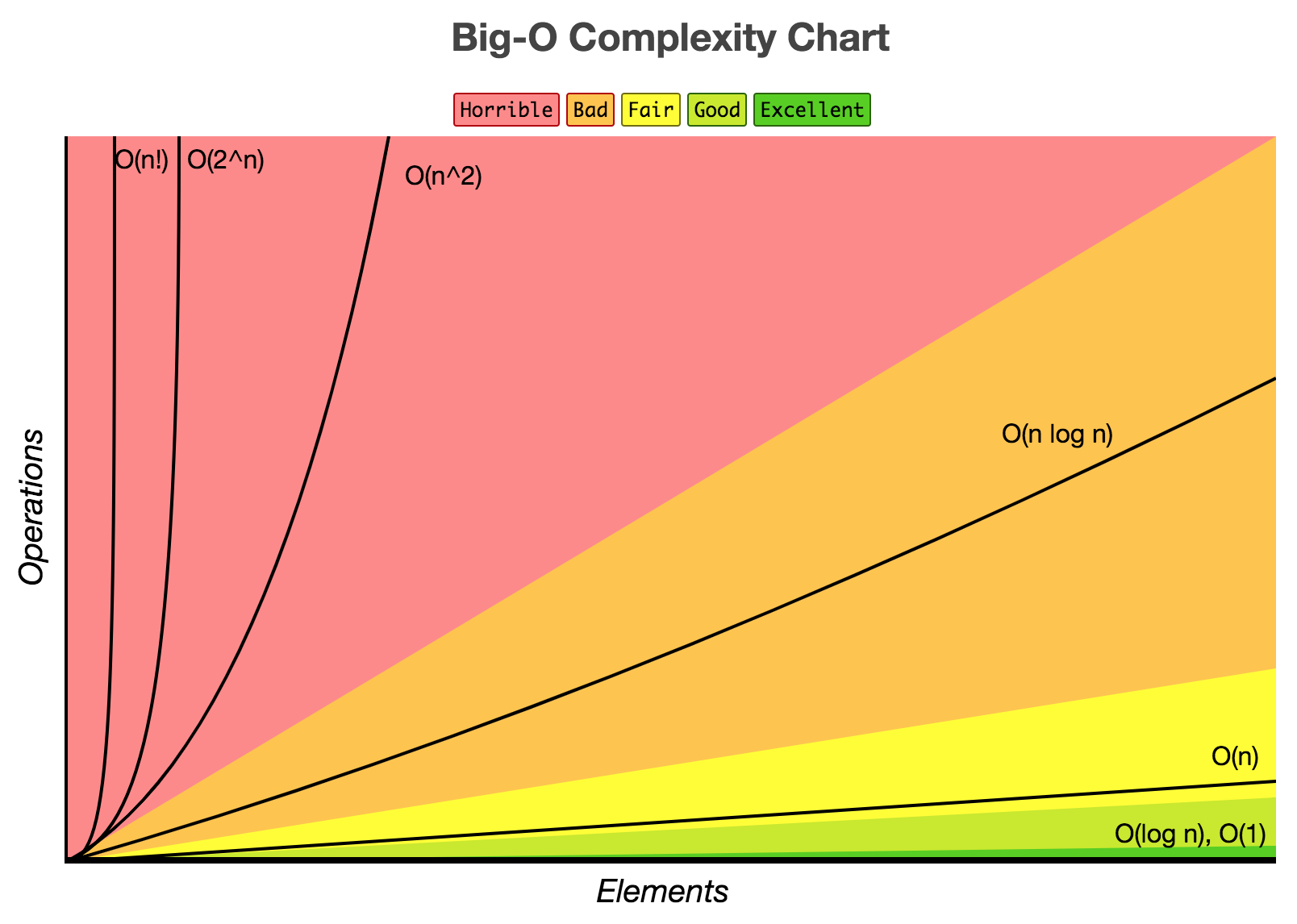
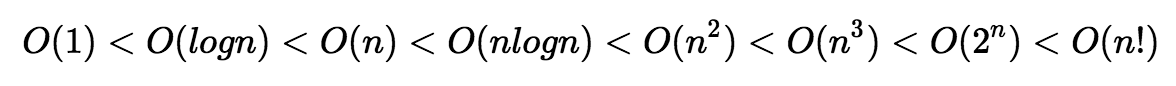
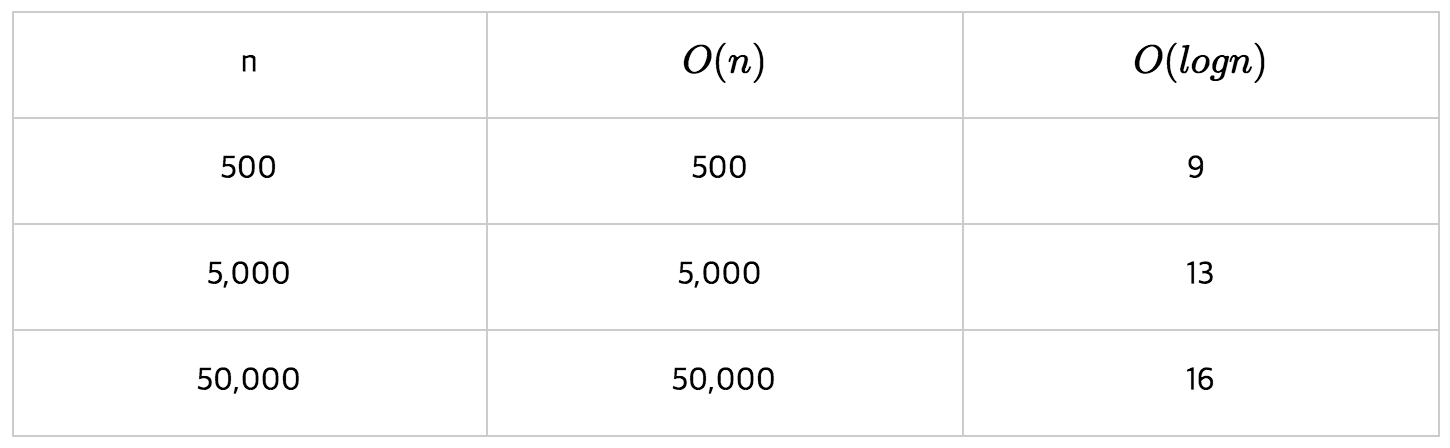
연산 횟수를 카운팅할 때 3가지 경우가 있다.
- Best Case
- Worst Case
- Average Case
평균적인 경우가 가장 이상적 But 알고리즘이 복잡해질 수 록 평균적인 경우는 구하기가 매우 어려워지며, 최악의 경우로 알고리즘의 성능을 파악한다.
Elementary Operation
프로그램의 진행 정도를 나타내는 기본 단위이다.
- 대입연산
- 사칙연산
- 비교구문
- 함수호출
알고리즘의 실행 순서를 따라가며 Elementary Operation이 일어나는 수를 측정한다.
1. 전역변수를 사용하여 Elementary Operation을 카운팅
let count = 0;
function sum(list, n) {
let tempSum = 0; // 대입연산
for (let i = 0; i < n; i++) {
count++; // loop 한번 돌 때마다
tempSum += list[i];
count++; // 대입연산
}
count++; // for loop 끝날 때 한번
count++; // return 수행
return tempSum;
} 2. 각 실행문 별로 Step 수와 실행 횟수를 분석한다.
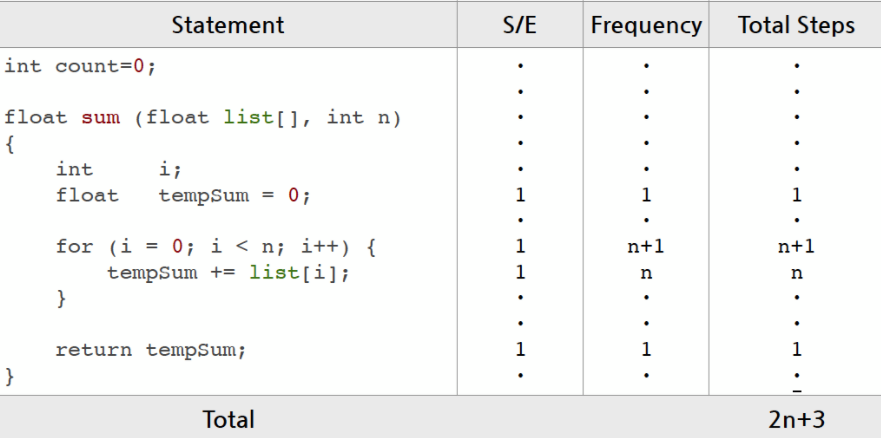
주어진 프로그램 2개의 성능 비교 및 분석
- 프로그램 P1의 성능 : C1 n^2 + C2 n
- 프로그램 P2의 성능 : C3 * n
C1, C2, C3에 따라서 대소 비교 결과가 다름.어떤 C1, C2, C3에 대해서도 C1 n^2 > C3 n을 만족하는 n은 존재함.
n이 작으면 프로그램 P1의 성능이 더 좋을 수도 있다.n이 충분히 크면 항상 프로그램 P2의 성능이 좋다. (P1에는 n이 제곱이기 때문에)
작은 경우 모두 성능이 좋으므로 문제될 것은 없다.따라서 n이 큰 경우의 처리가 중요하다.
참조
https://blog.chulgil.me/algorithm/
https://feel5ny.github.io/2017/12/09/CS_01/
