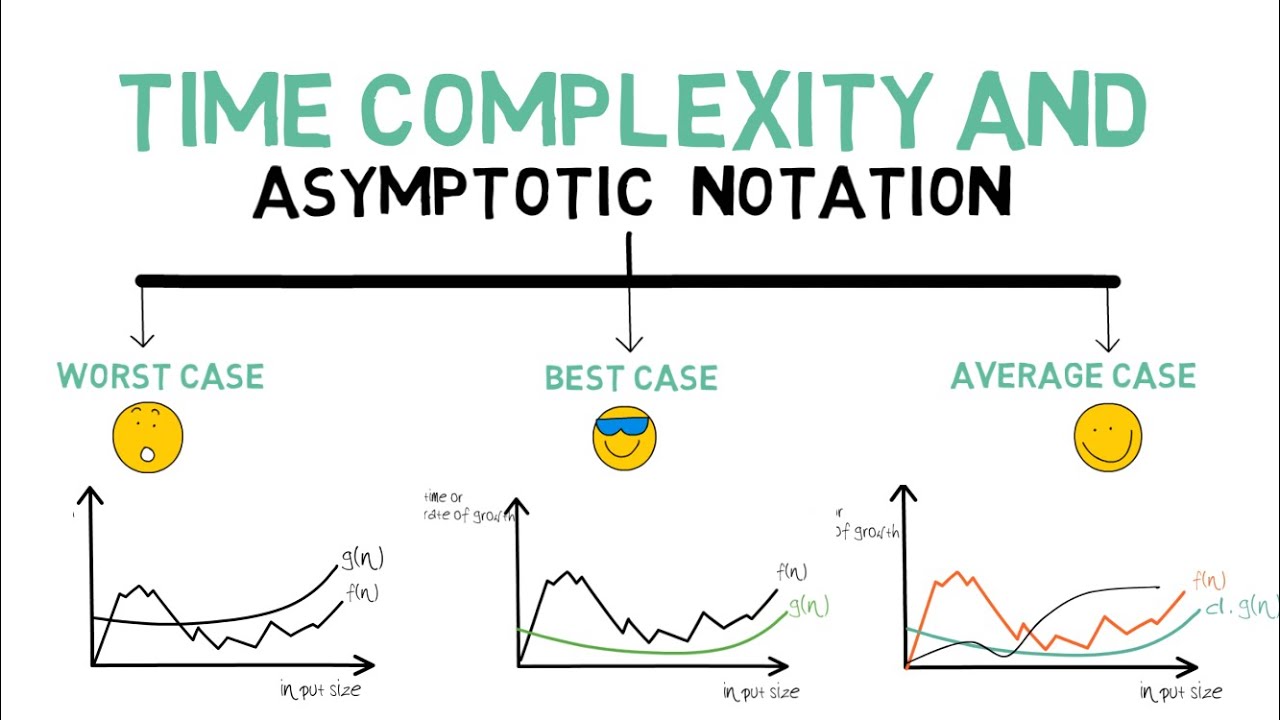
Asymtotic notation(점근적 표기법)
중요하지 않은 상수와 계수들을 제거하면 알고리즘의 실행시간에서 중요한 성장률에 집중할 수 있는데 이것을 점금적 표기법(Asymptotic notaion)이라 부른다.
점근적이라는 의미는 가장 큰 영향을 주는 항만 계산한다는 의미이다.
- 알고리즘의 실행시간은 컴퓨터가 알고리즘 코드를 실행하는 속도에 의존한다.
- 컴퓨터의 처리속도, 사용된 언어종류, 컴파일러 속도에 달려있다.
- 배열의 크기가 커지면 선형 검색과 이진 검색의 최대 추측 횟수가 함께 증가한다.
- 입력값의 크기에 따라 알고리즘의 실행시간 검증해볼 수 있다.
- 입력값의 크기에 따른 함수의 증가량 → 성장률(rate of growth)이라고 부른다.
6n^2+100n+3006, 이라는 기계 명령을 받는다고 가정하자.
n값이 어느 정도 커지면(이 경우는 20) 나머지 항목인 100n + 300 보다 커지게 된다.
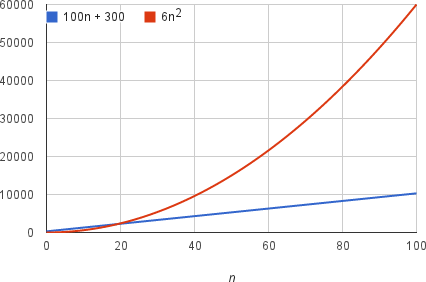
중요하지 않은 항과 상수 계수를 제거하면 이해를 방해하는 불필요한 부분이 없어져 알고리즘의 실행시간에서 중요한 부분인 성장률에 집중할 수 있다.
상수 계수와 중요하지 않은 항목을 제거한 것을 점근적 표기법(Asymtotoic notation) 이라고 한다.
점근적 분석의 필요성
어떠한 문제 해결을 위한 알고리즘의 성능분석을 할 때, 주어지는 데이터의 형태나 실험을 수행하는 환경, 또는 실험에 사용한 시스템의 성능 등 다양한 요소에 의해 공평한 결과가 나오기 힘들고 비교 결과가 항상 일정하지 않을 수 있다.
이를 효과적으로 해결하는 방법이 점근적 분석법이다.
점근적 분석법은 각 알고리즘이 주어진 데이터의 크기를 기준으로 수행시간 혹은 사용공간이 얼마나 되는지를 객관적으로 비교할 수 있는 기준을 제시하여 준다.
O(빅오), Ω(오메가), Θ(세타)등이 있다. 일반적으로 빅오와 세타표기가 많이 사용된다.
점근적 표기법
점근적 표기법은 세가지가 있는데 시간 복잡도를 나타내는데 사용된다.
- 최상의 경우: 오메가 표기법 (Big-Ω Notation)
- 평균의 경우: 세타 표기법 (Big-θ Notation)
- 최악의 경우: 빅오 표기법 (Big-O Notation)
빅오 표기법 O Notation
-
점근적 상한선(Asymptotic upper bound)
-
주어진 알고리즘이 아무리 나빠도 비교하는 함수와 같거나 좋다.
-
정의 : O(g(n)) = {f(n) : there exist positive constants c and n0 such that 0≤f(n)≤cg(n) for all n≥n0}n0를 기준으로
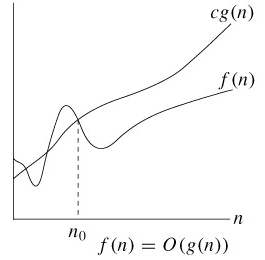
n0보다 오른쪽에 있는 모든 n 값에 대해 함수 f(n)은 함수 cg(n)보다 작거나 같다는 의미이다. 그래프가 아래에 있을 수록 수행시간이 짧은 것이므로 성능이 좋은 것이다.
오메가 표기법 Ω Notation
- 점근적 하한선(Asymptotic lower bound)
- 주어진 알고리즘이 아무리 좋아도 비교하는 함수와 같거나 나쁘다.
- 정의 : Ω(g(n)) = {f(n) : there exist positive constants c and n0 such that 0≤cg(n)≤f(n) for all n≥n0}
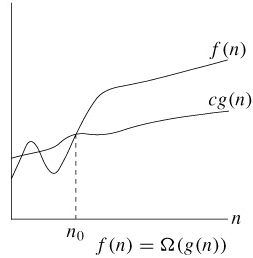
n0를 기준으로 n0보다 오른쪽에 있는 모든 n 값에 대해 함수 f(n)은 함수 cg(n)보다 크거나 같다는 의미이다.
세타 표기법 Θ Notation
- 점근선 상한선과 점근적 하한선의 교집합(Asymptotic tighter bound)
- 주어진 알고리즘이 아무리 좋아지거나 나빠지더라도 비교하는 함수의 범위안에 있다.
- 정의 : Θ(g(n)) = {f(n) : there exist positive constants c1, c2 and n0 such that 0≤c1g(n)≤f(n)≤c2g(n) for all n≥n0}
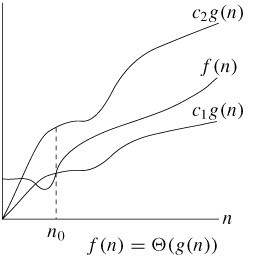
n0보다 오른쪽에 있는 모든 n 값에 대해 함수 f(n)은 함수 c1g(n)보다 크거나 같거나 c2g(n)보다 작거나 같다는 의미
참조
(https://blog.chulgil.me/algorithm/)
(https://feel5ny.github.io/2017/12/09/CS_01/)
(https://www.bigocheatsheet.com/)