Algorithim 24 : 연결된 정점들

설명

방향이 없는 간선들의 목록이 주어질 때, 연결된 정점의 컴포넌트(그룹들)가 몇 개인지 반환하는 함수를 작성하세요.

예시

const result = connectedVertices([
	[0, 1],
	[2, 3],
	[4, 5],
]);
console.log(result); // 3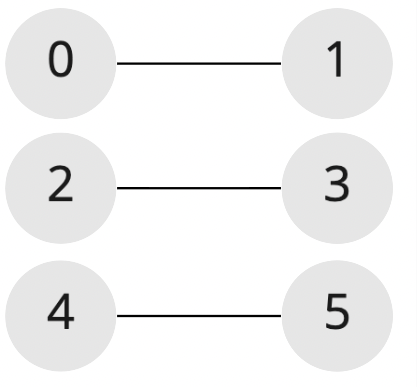

const result = connectedVertices([
	[0, 1],
	[2, 3],
	[3, 4],
	[3, 5],
]);
console.log(result); // 2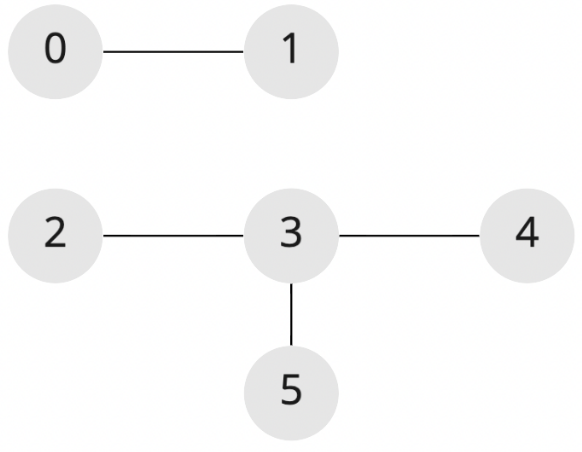

생각

bfs를 통해 시작점으로부터 같은너비에 방문할 수 있는 점들을 찾은 다음, bfs문이 끝나면 카운트를 해서 정점을 묶어서 리턴한다는 생각을 갖자.

풀이

//bfs문 생성 기본적으로 이 코드는 외워야 한다.
function bfs(matrix, from, isvisited) {
  let queue = [from]
  isvisited[from] = true
  while (queue.length > 0) {
    let now = queue.pop()
    for (let i = 0; i < matrix[now].length; i++) {
      if (matrix[now][i] === 1 && !isvisited[i]) {
        queue.unshift(i)
        isvisited[i] = true
      }
    }
  }
}
// 행렬을 만들고, 방문여부 변수를 만들어준다.
function connectedVertices(edges) {
  // TODO: 여기에 코드를 작성합니다.
  let maxNum = edges.flat()
  let maxVertex = Math.max(...maxNum)
  let matrix = new Array(maxVertex + 1).fill(0).map(item => new Array(maxVertex + 1).fill(0))
  let isvisited = new Array(matrix.length).fill(false)

for(let i=0; i<edges.length;i++){
  matrix[edges[i][0]][edges[i][1]] = 1
  matrix[edges[i][1]][edges[i][0]] = 1
}
  let count = 0;
//i번째 행을 방문한 적이 없다면 bfs 재귀함수 실행.
  for (let i = 0; i < matrix.length; i++) {
    if (!isvisited[i]) {
      bfs(matrix, i, isvisited)
      count++
    }
  }
  return count
}

//dfs로 푸는 방법. 얘도 외워주도록 하자.
function dfs(matrix, from, isvisited) {
  isvisited[from] = true
  for (let i = 0; i < matrix[from].length; i++) {
    if (matrix[from][i] === 1 && !isvisited[i]) {
      dfs(matrix, i, isvisited)
    }
  }
}

function connectedVertices(edges) {
  // TODO: 여기에 코드를 작성합니다.
  let maxNum = edges.flat()
  let maxVertex = Math.max(...maxNum)
  let matrix = new Array(maxVertex + 1).fill(0).map(item => new Array(maxVertex + 1).fill(0))
  let isvisited = new Array(matrix.length).fill(false)

for(let i=0; i<edges.length;i++){
  matrix[edges[i][0]][edges[i][1]] = 1
  matrix[edges[i][1]][edges[i][0]] = 1
}
  let count = 0;
//i번째 행을 방문한 적이 없다면 bfs 재귀함수 실행.
  for (let i = 0; i < matrix.length; i++) {
    if (!isvisited[i]) {
      bfs(matrix, i, isvisited)
      count++
    }
  }
  return count
}

깨달은 점

계속해서 bfs, dfs를 코드로 작성하지 못하고 이해하지 못해서 포기하고 있었는데, 열정적인 페어분과 함께 코드 한줄한줄 이해하려 노력하니 풀 수 있었다. for문에서 방문여부와 시작정점과 연결된 요소를 찾기 위해 isivited[i]와 matrix[now]를 사용했음을 이해했다.