TIL Day-24 그래프

Graph

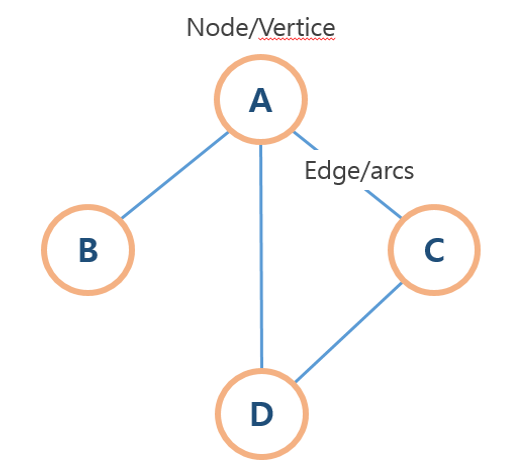
그래프 용어

• 노드(Node) : 정점(vertex)라고도 불리며 목적지를 나타내는 점을 말한다. 일반적으로 노드에는 데이터가 저장된다.
• 간선(edge) : 목적지와 목적지를 이어 주는 선.
• 무향(undirected) : 방향이 없기 때문에 간선으로 이어진 각 정점으로 이동할 수 있다.
• 유향(directed) : 방향이 정해져 있어 한 방향의 정점으로만 이동할 수 있다.
• 인접(adjacency) : 간선에 의해 연결된 정점을 말한다. 위 표를 통해 정점 A은 정점 B,C와 인접하다 말할 수 있다.
• 진입차수(in-degree) : 다른 노드로 부터 들어오는 간선의 수를 나타낸다.
• 진출차수(out-degree) : 다른 노드로 나가는 간선의 수를 나타낸다.

그래프 특징

• 그래프의 탐색방법에서 가장 중요한 것은 어떻게 하면 정점에 있는 자료를 효율적으로 찾을까? 이다.
  그래서 모든 정점들을 한 번씩 방문하는 방법이 크게 두 가지로 나뉜다.

BFS(Breadth First Search)

• 그래프에서 가장 가까운 노드부터 우선적으로 탐색하는 알고리즘이다.
• queue 자료구조를 사용하고 탐색 방법은 다음과 같다.

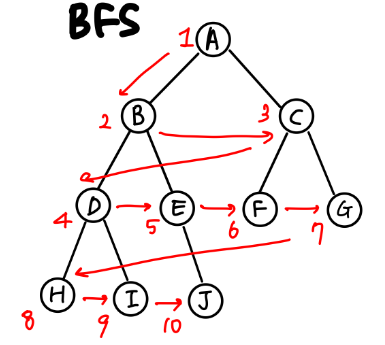
1. 번호가 낮은 노드부터 방문
2. 시작노드인 'A'를 방문처리
3. 'A'를 queue에서 꺼낸 후 인접노드 'B', 'C'를 방문처리
4. 'B'를 queue에서 꺼낸 후 인접노드 'D','E'를 방문처리
5. 'C'를 queue에서 꺼낸 후 인접노드 'F','G'를 방문처리

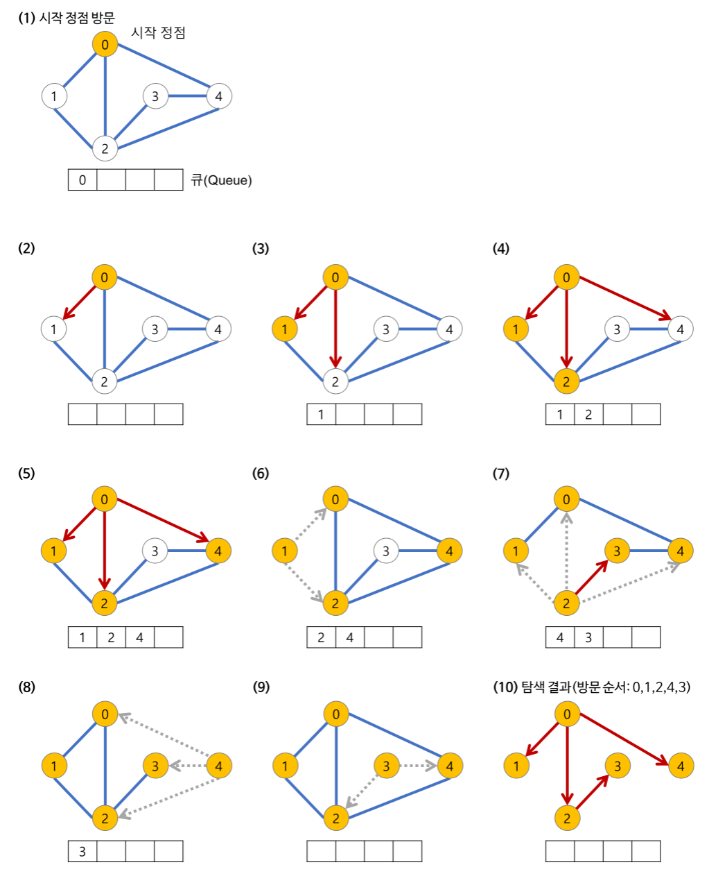
1. 시작노드인 0을 방문처리(queue에 추가)
2. 0을 queue에서 꺼낸 후 인접노드인 1,2,4 방문처리
3. 1을 queue에서 꺼낸 후 인접노드인 0,2 방문처리
4. 2를 queue에서 꺼낸 후 인접노드인 1,3 방문처리
   (기존에 방문한 노드는 추가하지 말고 새롭게 방문한 노드만 방문처리)
5. 인접한 노드가 없다면 queue 앞에서 노드를 꺼내 뒤에 삽입한다.
6. queue가 비어있을 때 까지 반복한다.

BFS의 장점

• 노드의 수가 적고 깊이가 얕은 경우 빠르게 작동한다.
• 현재 노드로부터 가까운 곳에서 부터 찾기 때문에 경로 탐색 시 먼저 찾아지는 해답이 곧 최단거리다.

BFS의 단점

• 재귀 호출을 사용하는 DFS와 달리 탐색할 노드를 queue에 저장해야 하므로 저장공간이 많이 필요하다.

BFS의 시간 복잡도

• 인접 리스트로 표현된 그래프 : O(N+E)
• 인접행렬로 표현된 그래프 : O(N^2)

DFS(Depth First Search)

• 그래프에서 해당 경로를 완벽하게 탐색할 때 사용하는 방법으로 깊이 우선 탐색이라고도 한다.
• stack 자료구조로 많이 쓰인다.

DFS의 장점

• 현재 경로상의 노드들만 기억하면 되므로, 저장 공간의 수요가 비교적 적다.
• 목표 노드가 깊은 단계에 있는 경우 해를 빨리 구할 수 있다.
• 구현이 너비 우선탐색보다 간단하다(?)

DFS의 단점

• 단순 검색속도는 BFS보다 느리다.
• 해를 구하면 탐색이 종료되므로, 구한 해가 최단 경로가 아닐 수 있다. (다른 경로에 적은 깊이에 해가 있는 경우)

DFS의 시간복잡도

• 인접 행렬로 표현된 그래프 : O(N^2)
• 인접 리스트로 표현된 그래프 : O(V+E)