1강 목차.

1-1. Digital Computer
Digital Computer = Digital System

1-2. Logic Gates
모든 Digital System은 Logic Gates로 이루어져 있다.
즉 Logic Gates는 Digital System의 기본 단위이다.

1-3. Boolean Algebra ( 이진 대수식 )
이진 대수식을 사용하여 회로를 표현하고 간소화할 수 있다.

1-4. Map Simplification
회로를 간소화하는 또 한가지의 방법.

1-5. Combinational Circuits ( 조합 회로)
결과값이 입력값에 의해서만 결정되는 논리 회로.

1-6. Flip-Flops
한 Bit를 기억하는 기억소자.

1-7. Sequential Circuits
Cominational Circuits와 Flip-Flops를 사용하면 Sequential Circuits를 만들 수 있다.

1-1. Digital Computer

0과 1을 사용하여 여러 계산을 수행하는 시스템
bit = 하나의 2진수.
컴퓨터는 이진수로 동작한다.

Ex. 1001011 ⇒ $1*2^6 + 0 * 2^5 + 0*2^4 + 1*2^3+0*2^2+1*2^1+1*2^0$

각각의 자릿수에 대한 Weight라고 생각할수도 있다.
컴퓨터는 하드웨어, 소프트웨어로 이루어진다.

• 하드웨어
  컴퓨터의 모든 전자부품과 주변장치를 구성하는 전자기적 부품
  하드웨어에서 가장 중요한 부품은 CPU와 RAM, IO Device
  1. CPU ( Central Process Unit )
     데이터를 조작하는 Arithmatic Logic Unit ( 산술 논리 장치), Register, 제어회로로 구성
  2. RAM ( Random Access Memory )
     명령어와 데이터를 저장하는 공간
  3. IO Device
     컴퓨터에 연결된 여러 입출력 장치들. Ex. 모니터, 키보드, 마우스...
     컴퓨터의 흐름은 다음과 같다.
     Input Devices → Input-Output Processor → RAM → CPU
     → RAM → Input-Output Processor →Output Devices
• 소프트웨어
  명령어와 데이터로 구성되어 작업을 수행하는 무형의 논리구조(?)
  ❗ 시스템 소프트웨어 ( 운영체제 ) ❗
  프로그램을 실행시키는데 필요한 Software Ex. Compiler or IO Device를 구동하는 Software

1-2. Logic Gates ( 논리 소자 )

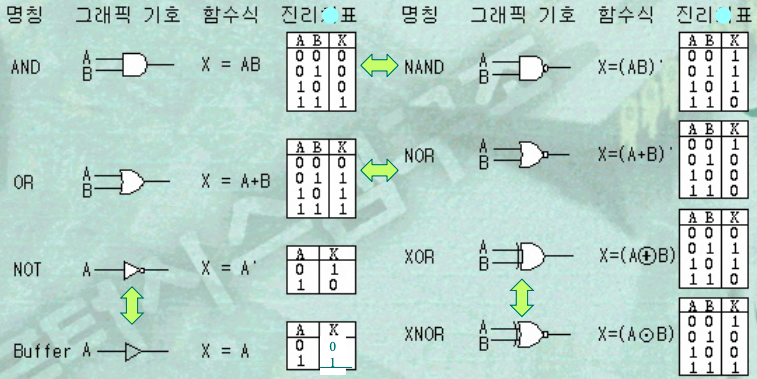
8개의 논리소자가 있음.
1. AND ⇒ X = AB
2. OR ⇒ X = A+B
3. NOT ⇒ X = A'
4. Buffer ⇒ X = A ❗신호의 세기를 복구하는 역할. ( 3.5V 이상 = 1, 1.5V 이하 = 0)
5. NAND ⇒ X = (AB)'
6. NOR ⇒ X = (A+B)'
7. XOR ⇒ X = A'B + AB'
8. XNOR ⇒ X = A'B' + AB

AND, OR, NOT을 이용하면 다른 소자의 기능을 만들 수 있다.

1-3. Boolean Algebra

논리소자들을 식으로 표현한 것. Ex. AND Gate ⇒ F(A,B) = AB
Boolean Function과 Logic Diagram과 Truth Table은 전부 같은 정보를 포함하고 있다. (회로의 기능)
Boolean Algebra를 사용하면 회로를 식으로 표현하고, 간소화 할 수 있다. ( 가장 적은 소자의 갯수로 같은 기능을 동작하는 회로를 만들 수 있다. )
부울 대수의 기본적인 관계에는 17개가 있다.

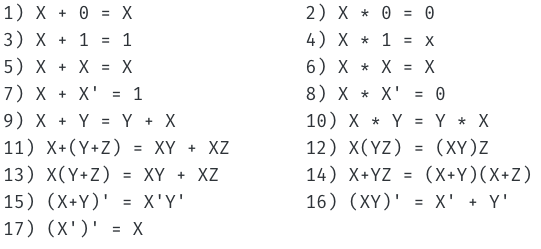
부울 대수의 기본적 관계

De Morgan's Theorem
어떤 수식에서 모든 OR 연산은 AND로, AND 연산은 OR으로 바꿔주고 각 변수를 보수화 한다.

Ex. F = AB+C'D'+B'D 일때
F' = (AB+C'D'+B'D)' = (AB)' (C'D')' (B'D)' = (A'+B') (C+D) (B+D')

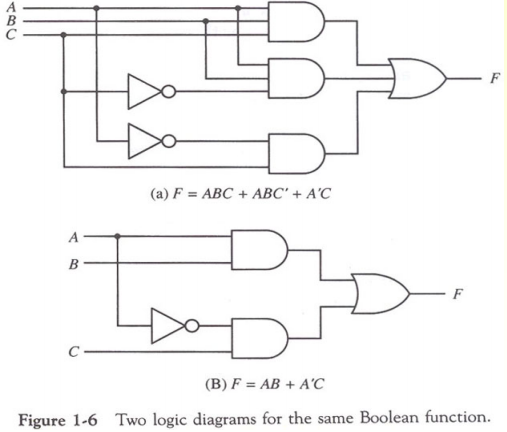
부울 대수를 사용하면 같은 기능을 하는 가장 간단한 소자를 그릴 수 있다.

Ex.

F = ABC + ABC' + A'C → X(Y+Z) = XY + XZ 공식 사용.
= AB(C + C') + A'C → C + C' = 1 공식 사용.
= AB*1 + A'C
= AB + A'C

논리소자 6개 → 논리소자 4개로 줄었다.