7.1 정렬이란?
탐색은 많은 자료 중에서 무언가를 찾는 작업이고, 정렬을 데이터를 순서대로 재배열 하는 것을 말한다. 효율적인 탐색과 정렬을 위해서는 적절한 자료구조가 반드시 요구된다. 정렬을 위해서는 우선 사물들을 서로 비교할 수 있어야 한다. 비교할 수 있는 모든 속성들은 정렬의 기준이 될 수 있다. 정렬시켜야 될 대상을 보통 레코드(record)라고 부른다. 또한 렝코드는 여러개의 필드로 이뤄진다. 이들 중에서 정렬의 기준이 되는 필드를 키(key) 또는 정렬 키(sort key)라고 한다. 결국 정렬이란 레코드들을 키 순서로 재배열하는 것이다.
정렬 장소에 따른 분류
- 내부 정렬: 모든 테이터가 메인 메로리에 올라와 있는 정렬을 의미.
- 외부 정렬: 외부 기억 장치에 대부분의 데이터가 있고 일부만 메모리에 올려 정렬하는 방법으로 대용량 자료를 정렬하기 위해 사용한다.
구현 복잡도와 알고리즘 효율성에 따른 분류
- 단순하지만 비효율적인 방법 : 삽입, 선택, 버블 정렬 등
- 복잡하지만 효율적인 방법 : 퀵, 힙, 병합, 기수 정렬 등
안정성에 따른 분류
안정성이란 입력 데이터에 동일한 키 값을 갖는 레코드가 여러 개 존재할 경우, 정렬 후에도 이들의 상대적인 위치가 바뀌지 않는 것을 말한다. 안정성을 충족하는 정렬에는 삽입, 버블, 병합 정렬이 있다.
7.2 간단한 정렬 알고리즘
선택 정렬(selection sort)
선택 정렬은 리스트에서 가장 작은 숫자를 선택해서 앞쪽으로 옮기는 방법. 전체 숫자들은 아직 정렬되지 않은 오른쪽 리스트와 정렬이 완료된 왼쪽 리스트로 나누어지는데, 맨 처음에 모든 숫자가 오른쪽 리스트에 들어와 있다. 선택 정렬은 오른쪽 리스트에서 가장 작은 숫자를 선택하여 왼쪽 리스트의 맨 뒤로 이동하는 작업을 반복하는 것이다. 다음 표같이 이 과정은 오른쪽 리스트가 공백 상태가 될 때까지 되풀이 된다.
실제로 선택 정렬을 구현하기 위해 두 개의 배열을 사용할 필요는 없다. 정렬이 안 된 리스트에서 최솟값이 선택되면 이 값을 배열의 첫번째 요소와 교환하면 되기 때문이다. 예를들어, 다른 그림에서 최솟값 1과 첫 번째 요소 5를 교환하면 전체 배열은 정렬된 부분과 되지 않은 부분으로 나뉜다. 다음에는 두 번째 요소부터 나머지들 중에 가장 작은 값을 선택하고 선택된 값을 두 번째 요소와 교환한다. 전체 요소의 개수가 n이면 이 절차를 n-1 번 반복하면 전체 리스트가 정렬된다.
선택정렬 알고리즘을 파이썬 함수로 구현한 코드는 다음과 같다.
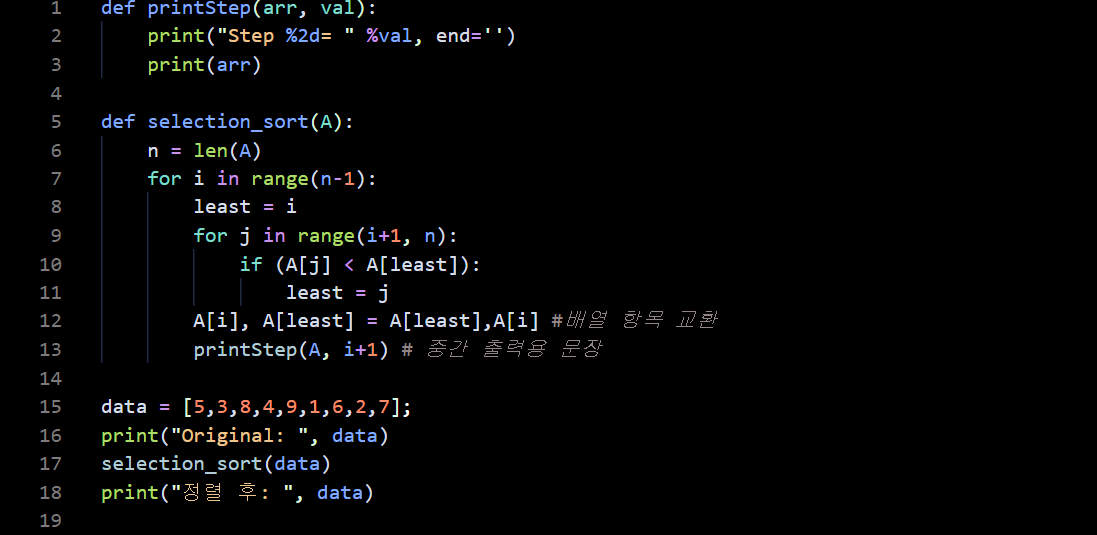
선택정렬은 입력 배열 이외에 추가적인 배열을 사용하지 않는다. 이러한 정렬 방법을 제자리 정렬(in-place-sorting)이라 한다. 선택 정렬의 시간 복잡도를 분석해보자. 이중 루프는 n-1번 반복, 내부 루프는 0에서 n-2까지 변하는 i에 대해서 n-1-i번 반복된다. 따라서 O(n²)이 된다. 결국 선택정렬은 효율적인 알고리즘도 아니고 안정성을 만족하지도 않는다. 그러나 알고리즘이 간단하고 입력자료의 구성과 상관없이 이동횟수가 결정된다는 장점이 있다.
삽입 정렬(insertion sort)
삽입 정렬은 카드를 정렬하는 방법과 유사하다. 손 안에 정렬된 카드가 있고 한장씩 새로 받을 때마다 끼워 넣는 것이다. 물론 삽입 후에도 전체 카드는 정렬되어 있어야 한다. 배열에서도 마찬가지이다. 정렬이 안 된 부분의 숫자를 하나씩 정렬된 부분의 적절한 위치를 찾아 끼워 넣는 과정을 반복. 한 번 삽입이 종료되면 정렬 안 된 부분의 항목수가 하나씩 줄어드는데 이 과정을 정렬 안 된 항목이 없을 때까지 반복하면 정렬이 끝난다.
그러나 숫자를 끼워넣는 과정이 문제다. 예를 들어, 4를 3과 5 사이에 삽입하기 위해서는 4보다 큰 항목들을 모두 한칸씩 뒤로 이동해야 한다. 이 과정은 정렬된 부분의 맨 뒤쪽항목부터 처리해야 하는 것에 유의.

삽입 정렬의 복잡도는 입력 자료의 구성에 따라서 달라진다. 먼저 입력자료가 이미 정렬되어 있는 경우는 가장 빠르다. 내부 루프가 모든 항목에서 한 번 만에 빠져나올 것이기 때문이다. 삽입 정렬의 외부 루프는 n-1번 실행되고 각 단계에서 1번의 비교와 2번의 이동만으로 이뤄지므로 총 비교 횟수는 n-1번, 총 이동횟수는 2(n-1)번이 되어 이 경우 시간 복잡도는 O(n)이다.
최악의 경우는 입력 자료가 역으로 정렬된 경우다. 각 단계에서 앞에 놓은 자료들은 전부 한 칸씩 뒤로 이동하여야 한다. 따라서 외부 루프안의 각 반복마다 i번의 비교가 수행. 이 때 비교 횟수는 n(n-1)/2 = O(n²) 특히 많은 레코드들의 이동을 포함하므로 레코드의 크기가 크고 양이 많은 경우 효율적이지 않다. 특히 대부분의 레코드가 이미 정렬되어 있는 경우 효율적으로 사용될 수 있다.
버블 정렬(bubble sort)
인접한 2개의 레코드를 비교하여 크기가 순서대로가 아니라면 서로 교환하는 방법을 사용한다. 이러한 비교-교환 과정은 리스트의 왼쪽 끝에서 시작하여 오른족 끝까지 진행한다. 비교-교환 과정이 한 번 완료되면(한 번의 스캔) 가장 큰 레코드가 리스트의 로른쪽 끝으로 이동된다. 이것을 마치 물속에서 거품이 보글보글하는 것과 유사해서 버블 정렬이라고 부른다.
리스트를 한번 스캔하면 오른쪽 끝에 가장 큰 레코드가 위치하게 되고 전체 리스트는 오른쪽의 정렬된 부분과 정렬이 안 된 왼쪽 부분으로 나뉜다. 이러한 수행은 더 이상 교환이 일어나지 않을 때까지 수행된다. 버블 정렬의 알고리즘은 다음과 같다. 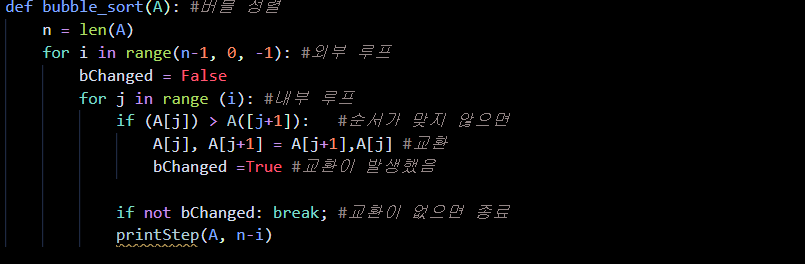
시간복잡도는? O(n²) 최선의 경우는 입력 자료가 이미 정렬되어 있는 경우로 한 번의 스캔만에 알고리즘이 종료된다. 매우 단순하지만 효율적이지 않다. 어느 정도 정렬되어 있는 경우에 효과적으로 사용될 수 있다.
정렬 응용(집합 다시 보기)
집합의 원소들을 어떻게 항상 정렬된 순으로 저장할 수 있을까? 집합의 원소들이 정렬되어 있으면 집합의 비교나 합집합, 차집한, 교집합 등을 훨씬 효율적으로 구현할 수 있다는 것이다.
삽입연산: insert
원소를 삽입하기 전 먼저 중복 검사를 해야 한다. 중복이 되었으면 삽입하지 않아야 한다. 이 때는 반드시 삽입할 위치를 먼저 찾아야 한다.

비교 연산:eq
두 집합이 같은 집합인지는 어떻게 비교할 수 있을까? 만약 정렬이 되어 있지 않은 상ㄴ태에서 두 집합 A와 B가 같은 집합인지를 판단하려면 A의 모든 원소가 B에 있고, 반대로 B의 모든 원소가 A에 있는지를 검사해야.
- 두 집합의 원소의 개수가 같아야 같은 집합
- 두 집합이 모두 정렬. 순서대로 같은 원소를 가져야 한다. 가장 작은 원소부터 하나씩 끝까지 서로 비교하여 모두 같아야 같은 집합
def __eq__(self, setB):
if self.size() != setB.size():
return False
for idx in range(len(self.items)):
if self.items[idx] != setB.items[idx]:
return False
return Trueeq()는 파이썬에서 미리 정의된 특별한 메소드로 == 연산자에 대한 연산자 중복 함수.
합집합 연산: union
합집합을 구하는 연산도 개선이 가능하다. 원소들이 크기순으로 정렬되어 있으면 한 번의 스캔만으로 합집합을 구현할 수 있다.
- 두 집합의 원소들이 크기순으로 정렬. 가장 작은 원소부터 비교해서 더 작은 원소를 새로운 집합에. 그 집합의 인덱스를 증가.
- 만약 두 집합의 현재 원소가 동일 -> 하나만을 새 집합에 넣으면 된다. 인덱스는 모두 증가
- 한쪽 집합이 모두 처리되면 나머지 집합의 원소를 순서대로 새 집합에 넣는다.
def union(self, setB):
newSet = set()
a = 0
b = 0
while a < len(self.items) and b < len(setB.items):
valueA = self.items[a]
valueB = setB.items[b]
if valueA < valueB:
newSet.items.append(valueA)
a += 1
elif valueA > valueB:
newSet.items.append(valueB)
b += 1
else:
newSet.items.append(valueA)
a += 1
b += 1
while a < len(self.items):
newSet.items.append(self.items[a])
a += 1
while b < len(setB.items):
newSet.items.append(setB.items[b])
b += 1
return newSet7.4 탐색과 맵 구조
탐색은 레코드(record)의 집합에서 원하는 레코드를 찾는 작업이다. 보통 이런 레코드들의 집합을 테이블(table)이라고 부른다. 레코드들은 서로를 구별하여 인식할 수 있는 키를 가지고 있는데 이를 탐색키(search key)라고 한다. 결국 탐색은 원하는 탐색키를 가진 레코드를 찾는 작업이다.
탐색에선느 테이블을 구성한는 방법에 따라 효율이 상이. 맵 또는 딕셔너리는 자료를 저장하고 탐색키를 이용해 원하는 자료를 빠르게 찾을 수 있도록 하는 탐색을 위한 자료구조. 맵은 엔트리라고 불리는 키를 가진 레코드(key record)의 집합. 엔트리는 두 개의 필드를 가진다.
- 키 : 영어단어나 사람 이름 같은 레코드를 구분할 수 있는 탐색키
- 값 : 영어 단어의 의미나 어떤 사람의 주소 같은 탐색키와 관련된 값
결국 맵은 키-값의 쌍으로 이뤄진 엔트리의 집합이다. 파이썬은 내장 자료형으로 딕셔너리를 제공. 이것은 자료구조 맵을 구현한 하나의 예이다. (파이썬 딕셔너리 구조를 떠올리자!)
Map ADT
데이터: 키를 가진 레코드(엔트리)의 집합
연산
- search(key): 탐색키 key를 가진 레코드를 찾아 반환한다.
- insert(entry): 주어진 entry를 맵에 삽입한다
- delete(key): 탐색키 key를 가진 렝코드를 찾아 삭제한다.
맵을 구현하는 여러 가지 방법들이 있다. 가장 간단한 방법은 엔트리들을 리스트에 저장하는 것이다. 이때, 엔트리들을 키값에 따라 정렬하여 맵을 만들 수도 있고, 정렬하지 않고 맵을 만들 수도 있다. 성능을 향상시키고자 한다면 이진탐색트리를 사용할 수 있다.(9장) 가장 좋은 방법은 해싱(hashing)이다.
간단한 탐색 알고리즘
순차 탐색(sequential search)
순차 탐색은 정렬되지 않은 테이블에서도 원하는 레코드를 찾을 수 있는 가장 단순하고 직관적인 방법으로, 테이블의 각 레코드를 처음부터 하나씩 순서대로 검사하여 원하는 레코드를 찾는다. 탐색을 위한 레코드들이 리스트에 저장되어 있을 떼, 탐색함수는
탐색 대상인 리스트 A와 탐색키 key
그리고 리스트에서의 탐색 범위 low, high를 매개변수로 전달받는다.
리스트의 low위치부터 탐색을 시작하여 성공하면 항목의 위치를 반환하다.
high까지 원하는 레코드가 나타나지 않으면 None을 반환한다.
def sequential(A, key, low, high):
for i in range(low, high+1): #low, low+1, ..., high
if A[i].key == key: #탐색이 성공하면
return i #인덱스를 반환
return None #탐색에 실패하면 None을 반환탐색의 성능을 살펴보자. 최선의 경우는 맨 앞에 있는 경우. 맨 뒤에 있거나 리스트에 없는 키를 찾는 경우 n이 최악이다. 평균적인 비교 횟수는
(1+2+ ...n)/n = (n+1)/2
결국 시간복잡도는 O(n)이다. 그러나 효율적이지않다.
이진탐색(binary search)
이진 탐색은 테이블의 중앙에 있는 갑승ㄹ 조사하여 찾은 항목이 왼쪽, 오른쪽에 있는지 판단한다. 찾는 항목이 왼쪽에 있다면 오른쪽은 탐색할 필요가 없고 그래서 매단계마다 검색해야 할 항목수가 반으로 줄어든다.
(1) 최초의 탐색 범위는 low=0 high = 15이다. 중앙위치 middle을 계산하고 이 위치의 값(27)이 키값보다 작으므로 low~middle 사이에는 34가 없다. 이제 low는 middle의 index + 1 이 된다. 탐색범위가 반으로 줄었다.
(2) 새로 계산한 middle의 위치의 값이 키갑보다 크다. 따라서 middle - high사이에는 찾느 값이 없다. 이제 high가 middlle-1이 되고 탐색의 범위는 다시 줄어든다.
(3) middle의 위치의 값이 키값보다 작다. 따라서 다시 low가 middle + 1이 된다.
(4) middle의 위치의 값(34)이 찾는 값이다. '
만약 찾는 값이 34가 아니라 33이라면 어떻게 될까? 4단계에서 다시 high가 middle-1이 된다. 그런데 low와 high가 역전된다. 이것은 찾는값이 없다는 것을 의미한다.
def binary_search(A, key,low, high):
if(low <= high):
middle = (low+high) // 2
if key == A[middle].key:
return middle #탐색 성공
elif (key < A[middle].key): #왼쪽 검색
return binary_search(A,key,low, middle-1)
else:
return binary_search(A,key,middle+1, high)
return None효율성을 위해선 반복구조가 더 유리하다
def binary_search(A,key,low,high):
while(low <= high):
middle = (low+high)//2
if key == A[middle].key:
return middle
elif(key > A[middle].key):
low = middle + 1
else:
high = middle - 1
return None탐색 범위가 반으로 줄어든다. 범위가 1이 될대 횟수를 k라 하면, n/2^k = 1 이 된다. 즉 k=log2n이므로 이진탐색의 시간 복잡도는 O(log2n)이 된다. 이진탐색은 매우 효율적이지만 반드시 배열이 정렬되어 있어야 한다. 그래서 삽입이나 삭제가 빈번한 응용에는 적당하지 않다.
보간탐색(interpolation Search)
탐색키가 존재할 위치를 예측하여 탐색하는 방법.
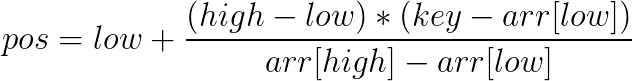
이 식은 탐색 값과 위치는 비례한다는 가정에서 탐색 위치를 결정할 때 찾고자 하는 키값에 근접하도록 가중치를 주는 방법이다.
(A[high] - A[low]) : (k-A[low]) = (high-low) : (탐색위치-low)
코드는 이진탐색 함수에서 middle 계산 코드만 다음과 같이 수정하면 된다.
middle = int(low + (high - low) * (key-A[low].key)/A[high].key - A[low].key
위치의 비율을 계산하기 위해서 실수 계산이 사용되지만 인덱스로 변경키 위해서는 반드시 정수로 변환해야 한다. 이진탐색과 동일한 시간복잡도를 갖지만 비교적 균등하게 분포되어 있는 자료의 경우 훨씬 효율적이다.
