컴퓨터 연산
1. 들어가기 🦔
컴퓨터 워드는 비트로 구성되어 있으므로 이진수로 표시할 수 있다. 그렇다면 소수나 실수는 어떻게 표현할까? 또한 실제로 어떻게 곱셈, 나눗헴을 수행할까?

🔗 우선 양수와 음수를 어떻게 표현하는지 살펴보자. 0들이 앞에 나오면 양수이고 1들이 앞에 나오면 음수가 되었다. 부호있는 이진수를 표현하는데 이러한 방식은 2의 보수(2's complement)표현법이라고 불린다.
전체의 절반인 양수0부터 2^31-1까지는 앞서와 같은 표현법을 사용한다. 그 다음 비트 패턴은(1000 0000(two)) 가장 큰 음수 -2^31을 나타내고 계속 작은 음수가 이어져서 -1(1111 1111)까지 감소한다.
2의 보수 표현에는 모든 음수는 MSB가 1이라는 장점이 있다. 따라서 하드웨어가 양수인지 음수인지 알아보려면 MSB만 검사하면 된다(0은 양수로 취급). 그러므로 MSB를 부호 비트(Sign bit)라고 부른다. 부호 비트의 역할을 이해하면, 2의 멱수를 곱한 값으로 32비트의 양수와 음수를 모두 표현할 수 있다.

2의 보수에서 사용할 수 있는 두 가지 빠른 계산법을 알아보자. 첫 번째는 2의 보수 이진수를 역부호화하는 빠른 방법이다. 모든 0을 1로, 1은 0으로 바꾸고 1을 더한다. 이 방식은 원래 수와 모든 비트를 역전시킨 수의 합은 111...111(two) 즉 -1이라는 데 기초하고 있다.

⚙️ 하드웨어 소프트웨어 인터페이스
부호있는 수와 부호가 없는 수는 산술연산뿐만 아니라 적재 명령어와도 상관이 있다. 부호있는 적재의 경우 레지스터의 남는 곳을 채우기 위해 부호를 반복하여 부호확장을 하게 된다. 이것의 목적은 레지스터 내부에 정확한 값을 적재하기 위함이다. 부호 없는 적재의 경우 데이터의 왼쪽을 0으로 채운다.
32비트 레지스터에 32비트 워드를 적재할 경우 논의의 여지가 있다. 부호있는 적재와 부호없는 적재는 동일. MIPS는 바이트 적재를 위해 두 개의 명령어를 제공한다. lb(load byte)명령어는 바이트를 부호 있는 수로 간주하고 남은 24비트를 부호 확장하여 채운다. 반면에 lbu(load byte unsigned) 명령어는 부호 없는 정수를 다룬다. C프로그램은 바이트를 부호 있는 정수로 다루기보다는 대부분의 경우에는 문자를 위해 사용하므로 lbu명령어는 실제적으로 바이트 적재를 위해서만 사용된다.
2. 💡 덧셈과 뺄셈 💡
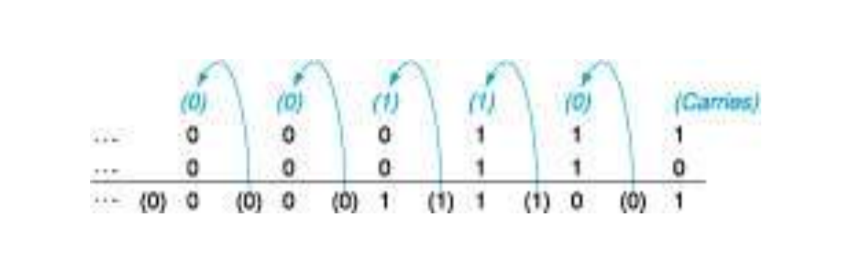
이진수의 덧셈, 올림수는 오른쪽 자리에서 왼쪽으로 이동한다. 계산 자체는 어렵지 않다. 그러나 사용가능한 하드웨어(이 경우 32비트 워드)로 표현할 수 없을 때 오버플로가 발생한다.
- 덧셈일 때 언제 오버플로우가 발생할까? 부호가 다른 피연산자를 더할 때는 발생하지 않는다.
- 뺄셈에서도 똑같이 오버플로가 발생하지 않는 경우가 있다. 단 뺄셈이므로 반대가 된다. 즉 피연사자의 부호가 같을 경우에는 오버플로가 발생할 수 없다. c-a = c+(-a)를 생각하면 된다. 같은 부호의 수를 빼는 것은 다른 수를 더하는 것과 같다. 아래는 오버플로우 발생 조건이다.
- A+B A >= 0 && B>=0, Result <0
- A+B A < 0 && B < 0, Result >=0
- A-B A >= 0 && B < 0, Result < 0
- A-B A < 0 && B >= 0, Result >= 0
컴퓨터 설계자는 연산 오버플로우를 어떻게 처리해야할 지 결정해야 한다. C나 Java의 경우 정수 오버플로를 무시하지만 일부 프로그램에서는 알려지그를 요구한다. MIPS는 오버플로우를 탐지하면 exeption을 발생시킨다.이는 본질적으로 계획도지 않은 프로시저 호출이다. 오버플로가 발생한 명령어의 주소는 레지스터에 저장되고 컴퓨터는 적다한 처리를 하기 위해서 해당 루틴으로 점프한다. 예외가 나온 주소를 저장해서, 해당 처리를 해준 다음에 프로그램 실행을 계속할 수 있게 해준다.
3.3 곱셈 🍞
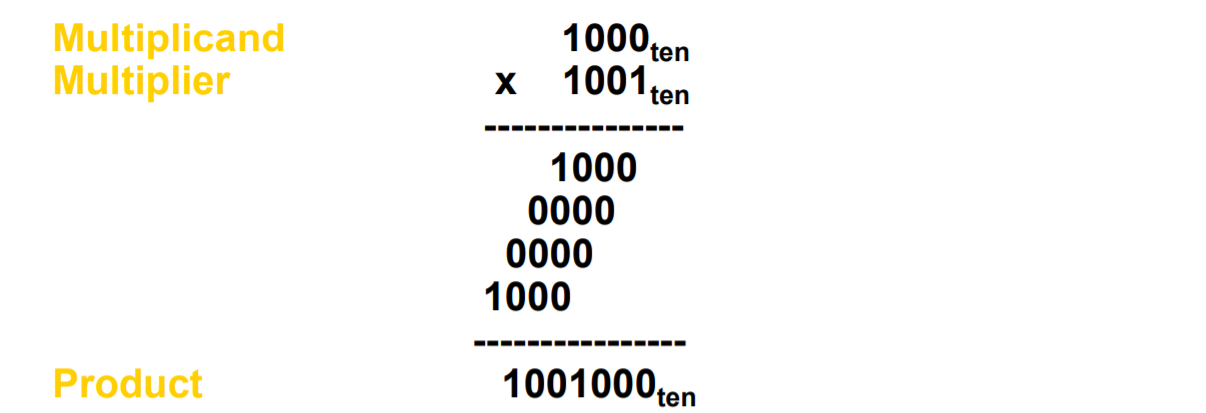
곱셈은 오히려 앞선 연산보다 쉬워보일 수도? 이후에 원리를 알아볼 때 정확하게 지칭하기 위해서 용어를 알아보자. 첫번째 피연산자는 피승수(multiplicand)라고 부르고 두번째 피연산자는 승수(multiplier)라고 부르며, 최종 결과는 곱(product)라고 부른다.
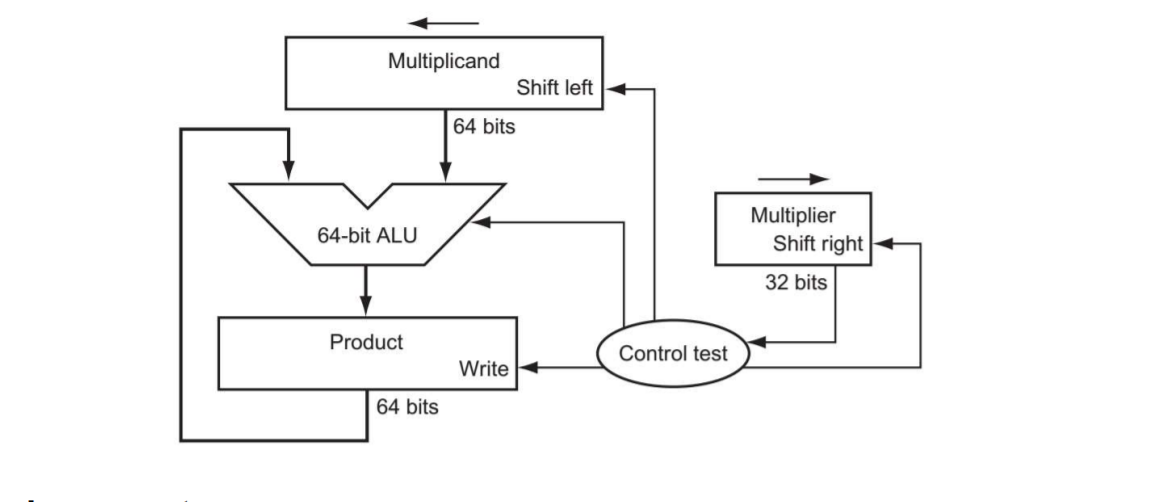
곱셈 하드웨어의 첫 번째 버전이다. 피승수 레지스터, ALU, 곱 레지스터는 모두 64비트. 승수 비트만 32비트이다. 시작할 때 32비트 피승수가 피승수 레지섵의 오른쪽 절반에 있다가 매 단계 마다 왼쪽으로 1비트씩 자리이동된다. 승수는 매 단계마다 반대 방향으로 자리이동된다. 승수의 최하위 비트가 1이면 피승수를 곱에 더한다. 그렇지 않으면, 다음 단계로 간다. 다음 두 단뎨에서 피승수를 왼쪽으로 자리이동시키고 승수를 오른쪽으로 자리이동시킨다.
⚙️ 하드웨어 소프트웨어 인터페이스
산술연산을 자리이동으로 대치시키는 것은 상수를 곱할 때에도 적용할 수 있다. 거의 모든 컴파일러가 2의 지수승을 곱하는 것을 왼쪽 자리이동으로 대치하는 강도 감소 최적화를(Strength reduction optimization)수행한다.
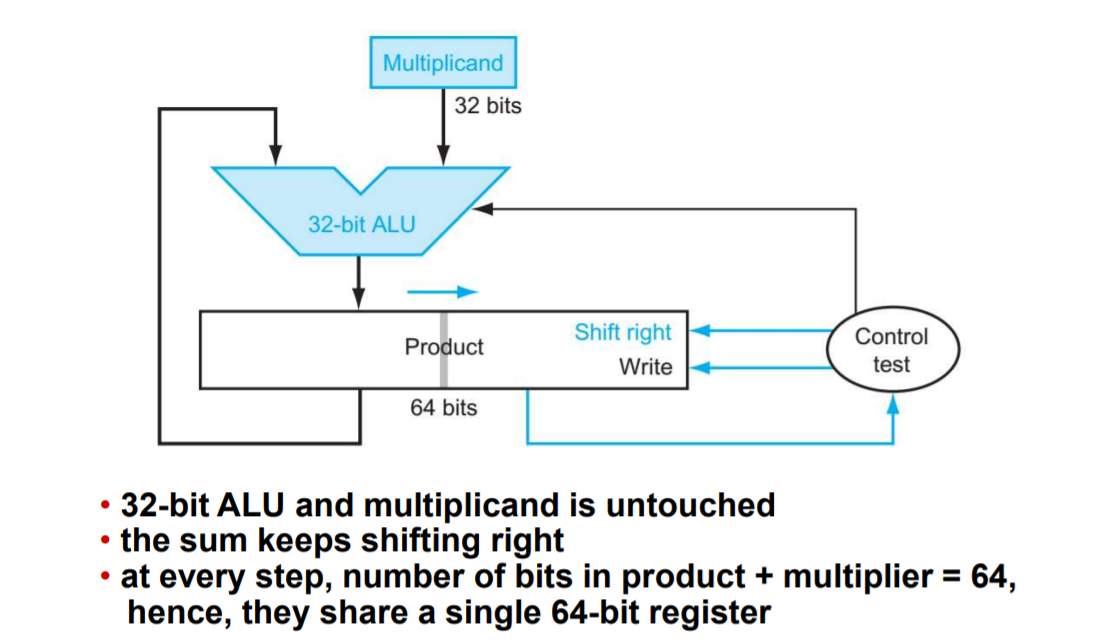
위의 것의 수정된 버전이다. 비교해보면 피승수, ALU, 승수 레지스터는 모두 32비트이고, 곱 레지스터만이 64비트이다. 이번에는 곱이 오른쪽으로 자리이동된다. 별도의 승수 레지스터는 없어졌다. 대신 승수를 곱 레지스터의 오른쪽 절반에 넣는다.
⚙️ 부호있는 곱셈
지금까지는 양수만을 다루었다. 부호있는 수의 곱셈을 가장 쉽게 이해할 수 있는 법은 먼저 승수와 피승수를 양수로 변환하고 원래의 부호를 기억하는 것이다. 이 알고리즘을 부호를 계산에서 제외시키고 31번 반복한 후, 피연산자들의 부호가 서로 다를 때만 곱을 음수로 바꾼다.
수는 무한히 많은 자리 수를 가질 수 있지만 우리가 32비트로 나타낼뿐임을 기억한다면, 마지막 알고리즘을 부호 있는 수의 곱셈에 사용할 수 있다. 부호 있는 수의 경우는 자리이동 단계에서 곱의 부호를 확장해야 한다. 알고리즘이 끝나면 아래쪽에 워드에 32비트 곱이 남게 된다.
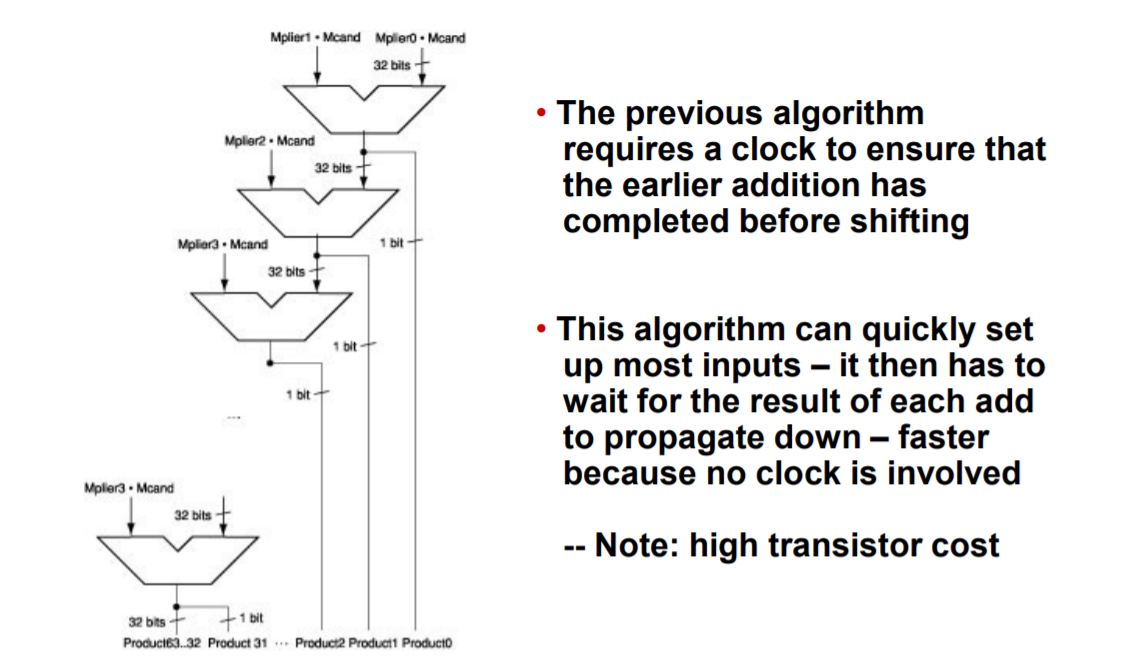
⚙️ 더 빠른 곱셈
Moore의 법칙을 하드웨어 설계자들이 훨씬 빠른 곱셈기를 만들 수 있도록 더 많은 자원을 제공해 왔다. 승수의 32개 비트를 각각 조사하면, 곱셈을 시작하는 초기에 이미 피승수가 더해져야 하는지, 아닌지를 알 수 있다. 승수의 매 비트마다 32비트 덧셈기를 하나씩 할당하면 더 빠른 곱셈이 가능하다. 덧셈기의 한 입력은 피승수를 해당 승수 비트와 AND한 것이고 다른 입력은 앞 덧셈기의 출력이다. 이렇게 더 많은 하드웨어를 사용하면 덧셈을 병렬로 더 빠르게 수행할 수도 있다.
🔥 3.4 나눗셈
사용빈도는 낮지만 훨씬 까다롭다. 특히나 0으로 나누기와 같이 수학적으로 유효하지 않은 연산을 요구하기도 한다.

나눗셈에서 피연산자는 피제수(dividend)와 제수(devisor) 두 개이고, 몫(quotient)이라 불리는 결과와 나머지(remainder)라고 불리는 두 번째 결과가 있다.
🔥 나눗셈 알고리즘과 하드웨어
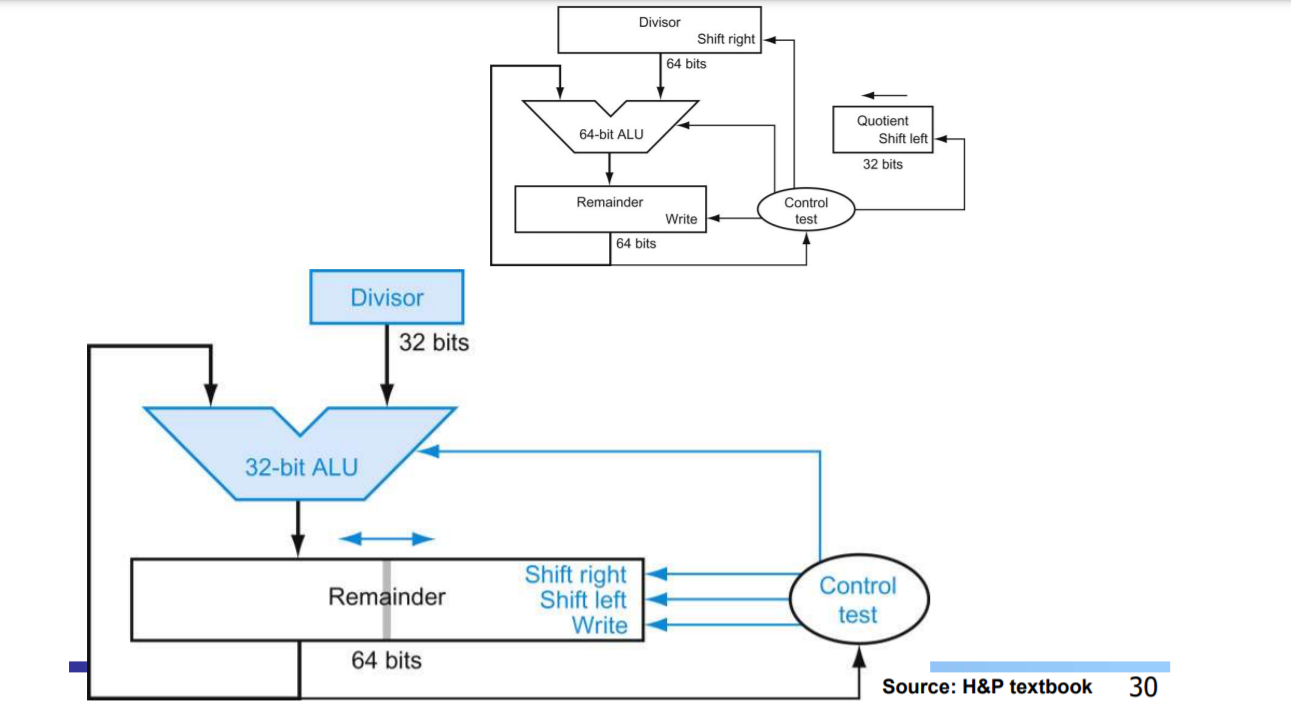
사람과 달리 컴퓨터는 제수가 피제수보다 작다는 것을 먼저 판단하지 못한다. 따라서 앞서 1에서 제수를 빼야만 한다.
🔥🔥 부호있는 나눗셈
지금까지 부호있는 나눗셈은 고려하지 않았다. 간단한 방법은 제수와 피제수의 부호를 기억하고 이 부호들이 다른 경우에는 몫을 음수화하는 것이다.
🔥🔥🔥 더 빠른 나눗셈
곱셈과 같이 나눗셈에도 Moore의 법칙이 적용될 수 있으므로 하드웨어를 추가해서 나눗셈 성능을 향상시킬 수 있다. 곱셈의 속도를 빠르게 하기 위해 많은 수의 덧셈기를 사용하였지만 같은 방법을 나눗셈에는 적용할 수 없다. 알고리즘의 다음 단계를 수행하기 전에 뺄셈한 결과의 부호를 알아야 하기 때문이다. 반면에 곱셈의 경우 32개의 부분곱을 바로 계산할 수 있다.
MIPS에서의 나눗셈

왼쪽이나 오른쪽으로 자리이동할 수 있는 64비트 레지스터와 덧셈과 뺄셈을 할 수 있는 32비트 ALU만 있으면 된다. MIPS는 곱셈과 나눗셈용 64비트 레지스터로 32비트 Hi와 Lo레지스터를 사용한다.
알고리즘에서 예측할 수 있듯, 나눗셈 명령이 완료된 뒤 Hi는 나머지를, Lo는 몫을 갖는다. 부호있는 정수와 부호없는 정수 모두를 다루기 위해서, MIPS에는 두 개의 명령어 div(divide)와 divu(divide unsigned)가 있다. MIPS어셈블리는 범용 레지스터 세 개를 사용하는 나누기 의사명령어를 제공. 이 의사 명령어는 mflo와 mfhi명령어를 사용해 원하는 결과를 범용레지스터에 넣는다.
🏊 부동소수점

프로그래밍 언어는 부호 있는 정수와 부호없는 정수 뿐만 아니라 소수 부분을 갖는 수도 다둘 수 있어야 한다. 수학에서는 이런 수를 실수(reals)라고 부른다. 위는 실수의 몇 가지 예시이다. 위에서 볼 수 있는 소수점의 왼쪽에는 한 자리 수만이 나타나게 하는 표기법을 과학적 표기법이라고 부른다. 이런 과학적 표기법 중에서 맨 앞에 0이 나오지 않는 것을 🔬정규화된 수(normalized number)라고 부른다.
이진수를 정규화된 형태로 표기하기 위해서는 0이 아닌 숫자가 한 자리만 나타나게 숫자를 자리이동한 후 자리 이동 횟수 만큼 증가시키거나 감소시킬 기수(base)가 필요하다. (컴퓨터에서는 당연히 2이다!) 기수가 10이 아니라서 앞으로는 이진 소수점(binary point)라고 이를 부를 것이다.
이런 수를 지원하는 컴퓨터 연산은 🏊부동 소수점(floating point) 연산이라고 한다. 왜냐하면 이러한 수에서는 정수에서와 달리 이진 소수점이 고정되어 있기 때문이다. C언어는 이러한 수를 나타내기 위해서 float이라는 변수형을 사용한다.
실수를 정규화된 형태의 표준 과학적 표기법으로 나나태면 세 가지 좋은 점이 있다.
- 첫째, 부동소수점 숫자를 포함한 자료의 교환을 간단하게 한다
- 둘째, 숫자가 항상 이렇게 표현되므로 부동소수점 산술 알고리즘이 간단해진다.
- 셋째, 불필요하게 선행되는 0을 소수점 오른쪽에 있는 실제 숫자로 바꾸기 때문에 한 워드 내에 저장할 수 있는 수의 정밀도를 증가시킨다.
🏊 부동소수점 표현
부동소수점 표현 방식을 설계하는 사람을 소수부분(fraction)의 크기와 지수(exponent)의 크기 사이에서 타협점을 찾아야 한다. 고정된 워드의 크기를 사용하기 때문이다. 소수부분의 크기를 증가시키면 정밀도가 증가하지만 지수의 크기를 증가시키면 표현할 수 있는 수의 범위가 늘어난다. 부동소수점 수의 크기는 보토 워드 크기의 배수이다. MIPS의 부동 소주점 표현은 아래 그림과 같다.

- s는 부동소수점 수의 부호이고(1=음수)
- 지수는 8비트 지수 필드의 값이며
- 소수부분은 23비트 수이다.
이와 같은 표현 방식은 부호 크기(sign and magnitude)표현 방식이라고 불린다. 부호가 수의 나머지부분과 떨어져 독립된 비트로 표현되기 때문
일반적으로 부동소수점 수는 다음과 같은 형태를 갖는다.
(-1)^S X F X 2^E
F는 소수부분의 값과 관련이 있고, E는 지수 부분의 값과 연관이 있다. 여기서도 오버플로가 발생할 수 있는데 이는 양수 값을 갖는 지수가 지수 부분에 표현될 수 없을 만큼 큰 상황을 의미한다. 반대로 언더플로는 음수 값을 갖는 지수가 부분에 표현될 수 없을 만큼 큰 상황이다.

언더플로와 오버플로의 발생 가능성을 줄이는 방법으로 지수 부분이 더 큰 다른 표현 형식을 사용할 수 있다. C언어에서는 이것을 double이라고 부른다. 그리고 double 형식을 갖는 수의 연산을 2배 정밀도(double precision) 부동소수점 연산이라고 부른다. 앞서 설명한 표현 형식은 단일정밀도(single precision) 부동소수점이라고 한다.
2배 정밀도 부동소수점 수를 표현하면 아래와 같이 MIPS워드 2개가 필요. 여기서 s는 여전히 수의 부호. 지수는 11비트의 지수, 52비트는 소수부분.

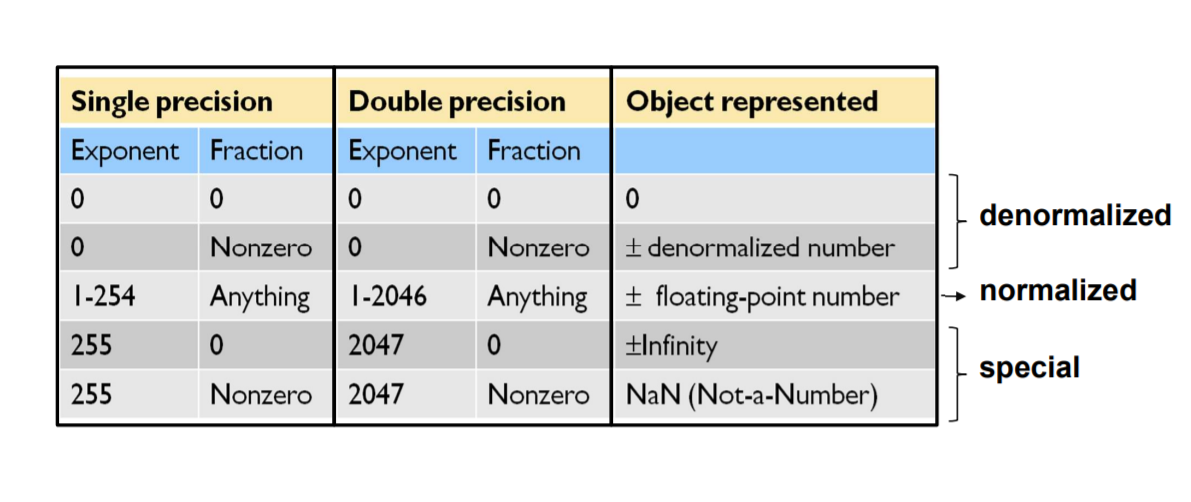
MIPS의 2배 정밀도 표현법의 주된 장점은 훨씬 더 큰 유효자리를 제공해서 정밀도를 높인다. 이런 형식은 MIPS의 고유한 것이 아니라 IEEE 754 부동소수점 표준으로서 모든 컴퓨터에 적용되고 이며 대부분의 형식은 아래와 같다.

IEEE 754는 0나누기 0이나 무한대 빼기 무한대와 같은 유효하지 않은 연산의 결과를 위한 심벌도 가지고 있다. 이 심벌은 NaN(NOT a Number)을 표현하는 NaN이다. 또한 IEEE 754설계자들은 정수 비교에 의해 쉽게 정렬될 수 있는 부동소수점 표현을 원했다. 이런 이유로 less than, greater than 또는 equal to 0를 빠르게 할 수 있도록 부호 비트가 최상위 비토에 놓였다.
하지만 음수 지수는 숫자 정렬을 어렵게 만든다. 만약 음수를 나타내기 위해 2의 보수법이나 지수 최상위 비트를 1로 만드는 표현법을 사용한다면, 매우 큰 수처럼 보일 것이다.

1/2보다 2가 더 커보인다! 이상적인 표기법은 가장 음수인 지수를 000...000(two)로, 가장 양수인 지수를 11...11(two)로 표현하는 방법이다. 이와 같은 방식을 biased notation이라고 부른다. IEEE754의 단일 정밀도 표현 방식에서 바이스값 127을 사용한다. 따라서 -1은 -1+127(ten) 또는 126=0111 1110 이라는 비트 패턴으로 표현된다. 그리고 1은 1+127 또는 128 = 1000 0000로 표현된다.

🏊 부동소수점 덧셈
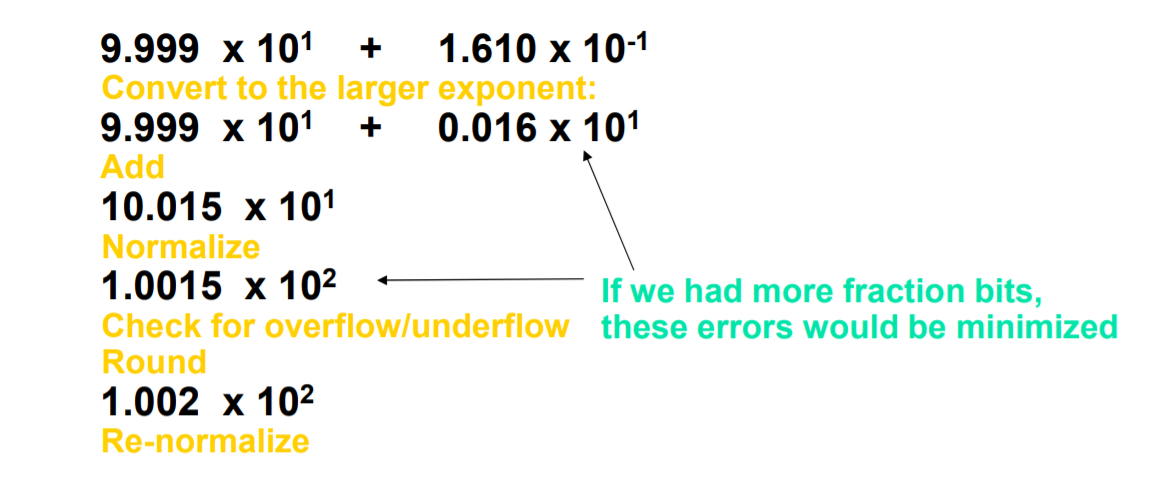
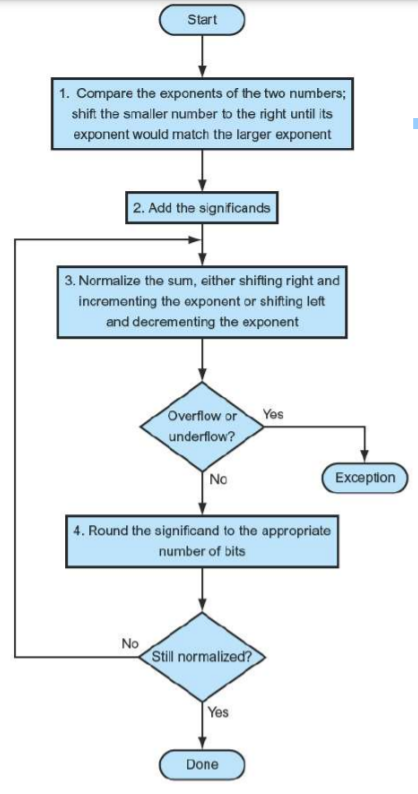
덧셈을 이해하기 위해서 위의 계산 과정을 살펴보자.
단계 1. 먼저 작은 지수를 갖는 수의 소수점을 지수가 큰 수에 맞춰 정렬. 1.610을 큰 지수와 일치하는 형태로 바꾸어야 한다.
단계 2. 유효자리를 서로 더한다. 합은 10.015 * 10^1
단계 3. 이 합은 정규화된 과학적 표기법이 아니므로 정돈할 필요가 있다. 이후의 과정들은 이를 보여준다.
단계 4. 유효자리가 네 자리라고 가정했기 때문에 수를 자리 맞춤 해주어야 한다.
🏊 부동소수점 곱셈
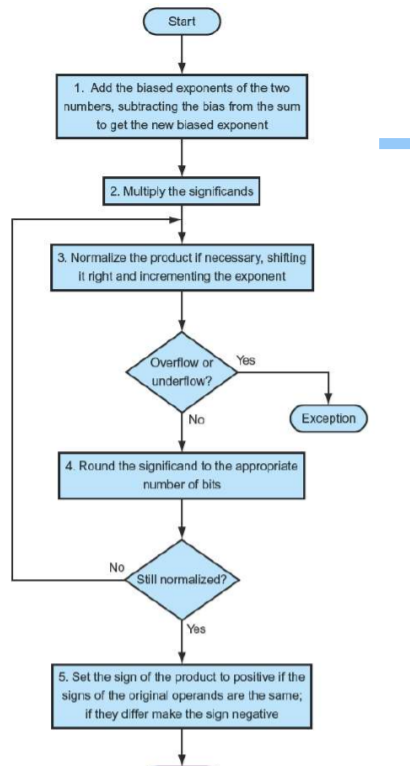
위의 그림처럼 곱셈은 방금 살펴본 십진 부동소수점 수의 곱셈과 매우 우수하다. 먼저 바이어스된 지수를 서로 더한 후 바이어스 하나를 빼서 곱의 새 지수를 구한다. 다음 단계는 유효자리들끼리의 곱이고, 이어서 필요에 따라 정규화 과정이 수행된다. 이후 오버플로나 언더플로가 발생했는지 검사해 결과를 자리맞춤한다. 만약 자리맞춤이 추가적으로 필요하면 한 번 더 크기를 검사한다. 마지막으로 피연산자들의 부호가 다르면 부호 비트를 1로 결정하고, 같으면 0으로 결정한다.
⚙️ MIPS의 부동소수점 명령어

MIPS는 다음과 같은 명령어를 사용하여 IEEE754 단일 정밀도 및 2배 정밀도 표현 형식을 지원한다. 단일 정밀도 +-*/에는 '.s'가 붙고 2배 정밀도 연산에는 '.d'가 붙는다. (ex add.s/ add.d) 이에 더해 부동소수점 분기로 참일때 분기(bc1t), 거짓일 때 분기(bc1f)가 있다.
부동소수점 비교는 비교조건에 따라서 cc(conditional code) 비트를 참(true)또는 거짓(false)로 정한다. 분기명령어는 cc값에 따라서 분기할 것인지 아닌지를 결정한다. MIPS의 설계자들은 $f0, $f1, $f2 ... 라고 불리는 부동소수점 레지스터를 별도로 두기로 했다. 이들은 단일 정밀도와 2배 정밀도 모두 사용된다. 이에 따라서 부동소수점 적재 및 저장 며령ㅇ어 lwc1과 swc1을 포함시켰다. 부동소수점 수의 적재와 저장 명령어는 주소 계산에서 사용되는 베이스 레지스터로는 정수 레지스터가 사용된다. 두 개의 단일 정밀도 수를 메모리에서 읽어 와서, 더한 값을 다시 저장하는 MIPS코드는 다음과 같다.
lwcl $f4, c($sp) #load 32bit F.P. number into F4
lwcl $f6, a($sp) #load 32bit F.P. number into F6
add.s $f2,$f4,$f6 #F2 = F4 + F6 single precision
swcl $f2, b($sp) #store 32bit F.P. number from F2
2배 정밀도 레지스터 하나가 사실은 단일 정밀도 레지스터 한 쌍을 합쳐서 사용하는 것.
이때 짝수번 레지스터 번소를 레지스터 이름으로 사용한다.
따라서 단일 정밀도 레지스터 $f2, $f3 한 쌍은 2배 정밀도 레지스터 $f2가 된다.
[추가 예시]