5.1 큐란?
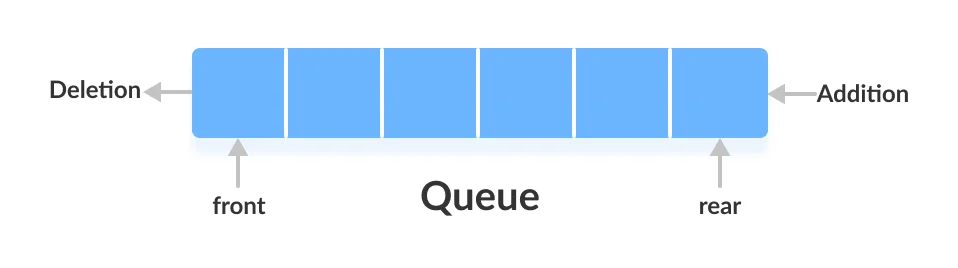
큐는 선입선출(First-In First Out:FIFO)의 자료구조이다.
선착순을 생각하면 쉽다. 먼저 들어온 데이터가 먼저 나간다. (군대) 구조상으로 큐가 스택과 다른 점은 삽입과 삭제 연산의 위치가 같은 곳에서 일어난다. 큐에서 삽입이 일어나는 곳을 후단(rear)라 하고 삭제가 일어나는 곳을 전단(front)라 한다.
큐 그거 어디 씀?
-
컴퓨터에서 데이터를 주고 받을 때 주변장치와 속도 차이를 위한 임시 기억장치로 쓰인다. 이것을 버퍼라고 한다. 컴퓨터와 프린터 사이에 인쇄 작업 큐가 존재.
-
프린터는 CPU에 비해 상대적으로 속도가 느리다. 따라서 CPU는 먼저 빠른 속도로 데이터를 만들어 프린터 큐에 보내고 다른 작업으로 넘어간다. 그럼 일정한 속도로 프린터가 인쇄 작업 큐에서 데이터를 가져와 실행시킨다.
-
실시간 비디오 스트리밍에서 다운된 데이터가 비디오를 재생하기에 충분하지 않으면 큐에 순서대로 모아두었다가 충분한 양이 되었을 때 비디오를 복원해서 재생한다. 이것이 버퍼링!
5.2 큐의 구현
선형 큐에는 어떤 문제가 있을까?
큐 항목을 저장하는 가장 쉬운 방법은 배열구조인 파이썬의 리스트를 사용하는 것이다.
Items = []맨 앞을 front라 하고 맨 뒤를 rear이라 하자. 이렇게 되면 front와 rear을 위한 변수를 따로 관리할 필요가 없다. front의index는 항상 0이요, rear은 항상 -1이기 때문이다.
isEmpty():공백상태검사
def isEmpty(): return len(itmes) == 0
enqueue(item): 삽입연산
삽입연산은 rear 항목에 항목을 추가. 젤 뒤에 넣어주자def enqueue(item): items.append(item)
dequeue(): 삭제연산
삭제 연산은 front에서 항목 하나 꺼내고 이를 반환. 맨 앞을 꺼내는 것은 pop()사용. 시간복잡도 n인거 checkdef dequeue(item): if not isEmpty(): return items.pop(0)
peek(): 반환연산
얘는 반환만하고 큐는 건드리지 않는다.def peek(): if not isEmpty(): return items[-1]
나머지 연산(size와 clear 등)들은 스택과 비슷하게 간단히 구현된다. 선형 큐에서는 삽입과 삭제 연산의 시간 복잡도를 1로 만들수 없다. 삭제연산도 1로 동작하도록 구현할 수는 없을까?
이것이! 원형큐를 위한 빌드업인데
사실 더 심각한 문제가 있다. 바로 계속해서 삭제와 삽입을 이어나가다 보면, front는 당겨지고 rear은 뒤로 밀리게 되는데 메모리가 가득 찰 때까지 하면, 이게 앞은 비어있는데 front가 계속 당겨져 앞이 아니게 되어버려 비어있는데도 왜 쓰질 못하니!가 된다.
5.3 🍩 원형 큐가 훨씬 효과적이다
배열이...선형이라고 생각하는 것도 어쩌면 고정관념이 아닐까요? 배열을 선형으로 생각하지 않고 원형으로 맨끝과 맨앞을 연결해보자. 실제 리스트가 원형이라는 것이 아니라 그렇게 구현하고 사용하는 것일 뿐이다.
원형 큐에서는 기본적으로 리스트의 크기가 고정되어야. C의 배열처럼 리스트에 항상 크기가 코정된(MAX_QSIZE)의 배열이 있다고 생각하자. 원형 큐에서는 front와 rear을 위한 변수가 필요. rear은 큐에서 가장 최근에 삽입된 항목의 '위치' front는 가장 최근에 삭제된 항목의 ⏬위치⏬를 저장한다.
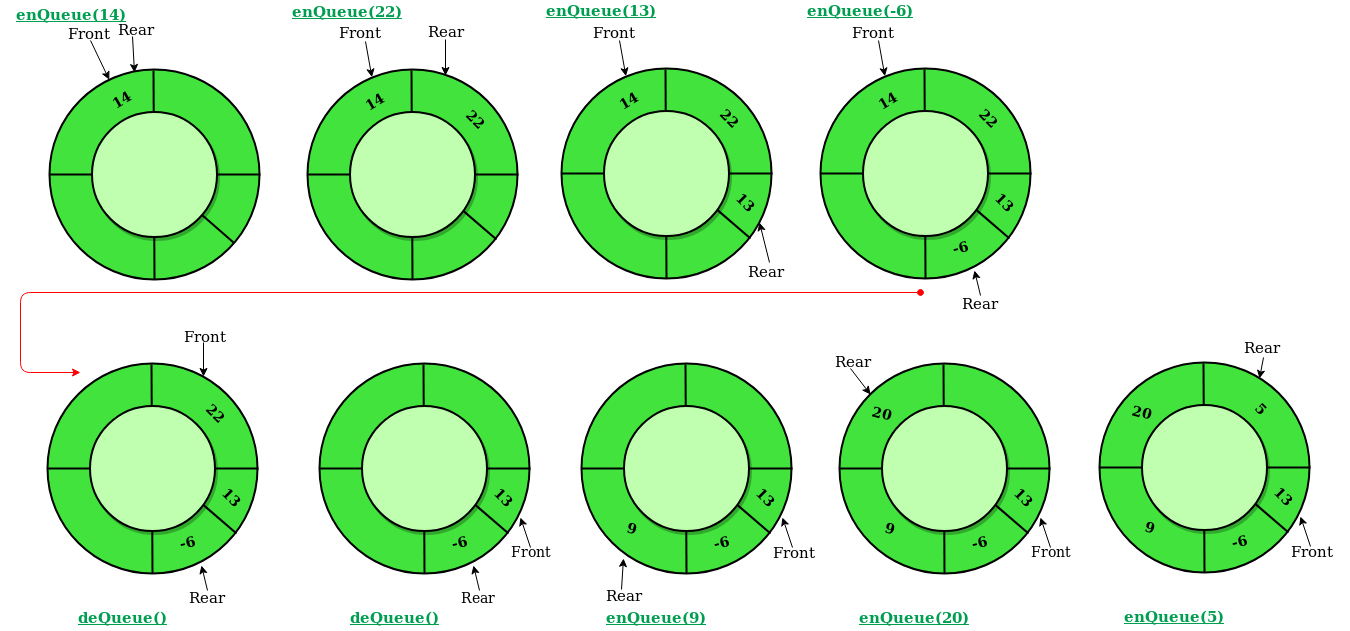
중요한 것은 인덱스가 원형으로 움직인다는 것. 0부터 계속 증가하다가 MAX_QSIZE-1이 되면 다음은 MAX_QSIZE가 아니라 다시 0이 된다. 그렇다면 어떻게 회전을 시킬까? 다음과 같이 나머지 연산자를 사용해보자.
front = (front+1) % MAX_QSIZE
rear = (rear+1) % MAX_QSIZE
삭제를 해도 항목들을 앞으로 하나씩 당길 필요가 없다. 삽입도 마찬가지. 인덱스만 즉 가리키는 것만 변경되기 때문에 삽입과 삭제 연산이 모두 O(1)이다.
큐의 상태
- 공백상태 공백상태는 초기처럼 front==rear인 경우이다. ⚠️ 이들이 반드시 0일 필요는 없다⚠️. 같은 곳만 가리키면 공백상태이다.
- 포화상태 선형 큐에서 포화상태를 정의하지 않았다. 쉽게 생각하면, '꽉 찬거 아님?'이라 생각할 수 있지만 그럼 공백과 같아진다. 그래서 front가 rear보다 하나 앞에 있으면 포화상태로 정의한다. 이것은 front == (rear+1) % MAX_QSIZE 인 상태를 의미.
원형 큐의 구현
이제 구현해보자!
MAX_QSIZE = 10 #최대 크기
class CircularQueue :
def__inint--(self):
self.front = 0
self.rear =0
self.item = [None] * MAX_QSIZE
#항목 저장용 리스트 [None,None...](빈칸 개념)
def isEmptpy(self): return self.front == self.rear;
def isFull(self): return self.front == (self.rear+1) % MAX_QSIZE
def clear(self): self.front == self.rear%MAX_QSIZE삽입, 삭제 및 peek연산은 다음과 같다. front와 rear을 원형으로 회전시키는 코드에 주의!
def enqueue(self, item):
if not self.isFull():
self.rear = (self.rear+1)%MAX_QSIZE
self.itmes[self.rear] = item
def dequeue(self, item):
if not self.isEmpty():
self.front = (self.front+1)%MAX_QSIZE
return self.items[self.front]
def peek(self):
if not self.isEmpty():
return self.items[(self.front+1)%MAX_QSIZE]
현재 큐에 저장된 항목의 개수는 어떻게 구할까? rear-front로는 충분하지 않다. 왜냐면 지금 원형이기 때문이다. 다음과 같이 큐의 크기 MAX_QSIZE와 모듈러 연산을 이용해야 한다.
def size(self):
return (self.rear - self.front + MAX_QSIZE)%MAX_QSIZE아직 끝난 것이 아니다. 큐의 내용을 출력하려면? 케이스를 나눠봐야한다.
-
f > r 인 경우 원을 나눈다. items[front+1:MAX_QSIZE] + items[0:rear+1]
-
f < r 인 경우 items[front+1 : rear+1]
def display(self):
out = []
if self.front < self.rear :
out = self.items[self.front+1 : self.rear+1]
else:
out = self.items[self.front+1 : MAX_QSIZE]
+ self.items[0:self.rear + 1]
🔥🔥 원을 반으로 쪼갠다고 생각하면 된다 🔥🔥
그렇다면 사용은 어떻게 할까?
q = CircularQueue()
for i in range(8): q.enqueue(i)
5.4 덱이란?
덱은 스택이나 큐보다는 입출력이 자유로운 자료구조이다.
덱은 double-ended queue의 줄임말로서 큐의 전단(front)과 후단(rear)에서 모두 삽입과 삭제가 가능한 큐를 의미한다. 그렇지만 덱도 중간에 삽입하거나 삭제는 안 된다.
Deque ADT
데이터 : 전단과 후단을 통한 접근을 허용하는 항목들의 모음
연산
- Deque(): 비어있는 새로운 덱을 만든다
- isEmpty(): 덱이 비어있으면 True 아니면 False를 반환한다
- addFront(x) : 항목 x를 덱의 맨 앞에 추가한다
- deleteFront() : 맨 앞의 항목을 꺼내서 반환한다
- getFront(): 맨 앞의 항목을 꺼내지 않고 반환한다
- addRear(x) : 항목 x를 덱의 맨 뒤에 추가한다
- deleteRear(): 맨 뒤의 항목을 꺼내지 않고 반환한다
- getRear(): 맨 뒤의 항목을 꺼내지 않고 반환한다
- isFull(): 덱이 가득 차 있으면 True 아니면 False를 반환한다
- size(): 덱의 모든 항목들의 개수를 반환한다
- clear(): 덱을 공백상태로 만든다.
덱은 스택과 큐의 연산을 모두 가지고 있다.
- 덱의 addRear, deleteFront, getFront 연산은 각각 큐의 enqueue, dequeue, peek 연산과 정확히 동일하다
- 덱의 후단(rear)을 스택의 상단(top)으로 사용한다면, 덱의 addRear, deleteRear, getRear연산은 스택의 push, pop, peek 연산과 정확히 동일하다.
덱은 구조상 큐와 더 비슷하다. 따라서 원형 덱으로 구현하는 것이 연산들의 시간 복잡도를 O(1)로 만들어 줄 수 있는 좋은 방법이다. 주의해야 할 연산은 front와 rear를 감소시켜야 하는 deleteRear와 addFront이다. 다음 그림과 같이 인덱스를 감소시키는 것은 반대 방향, 즉 반시계방향의 회전을 의미한다. front와 rear를 반대방향으로 회전시키는 코드는 다음과 같다.
front <- (front-1 + MAX_QSIZE) % MAX_QSIZE
rear <- (rear-1 + MAX_QSIZE) % MAX_QSIZE5.5 덱의 구현
원형 큐를 상속하여 원형 덱 클래스를 구현하자
상속이 나온다고 너무 겁먹을 필요 없다. 앞서 구현한 원형 큐 클래스 circularQueue를 상속하여 새로운 원형 덱 클래스 CircularDeque를 만들어 보자. 많은 기능들이 이미 CircularQueue에서 구현되었기 때문에 CircularDeque 클래스에서 작성해야 할 코드는 많지 않다.
class CircularDeque(CircularQueue): #서큐 상속상속 = 어감이 이상하지만 자식 안에 부모가 있는 것과 같다. 따라서 이 클래스는 이미 멤버 면수와 메소드를 가지고 있다. 그러나 생성자는 상속되지 않으니까 다시 정의해주자!
def __init__(self):
super().__init__()상속 나왔다고 쫄지말구 담대하자. 밑에서 하나씩 톺아보자
- 자식클래스에서 부모님 모셔오는 함수가 super()이다. (super쎄짐)
- 생성자에서 front, rear, items와 같은 거 선언 안함. 왜냐면 부모 클래스 데이터 멤버여서 이미 자식 클래스 내에 있다.
- 부모 클래스의 멤버들은 super()함수를 통해서도 사용할 수 있음! 예를 들어 super().front는 self.front와 동일하다.
- 생성자는 예외. 자식도, 부모도 생성자가 있으므로(=모두 태어나야 하므로) 부모의 생성자를 구분하기 위해서는 반드시 위와 같이 선언해줘야함!
- 그래서 isEmpty, isFull, size, clear와 같이 부모에서 구현된 연산들도 클래스에 구현되어 있다고 생각하고 그냥 쓰셈! ex) self.isEmpty()호출. 이렇게 코드로 재사용함.
그런데 자식 클래스에도 코드를 적어줘야 한다. 근데 두 번 고민하지 말고 구현은 되어 있다. 그래서 인터페이스만 잘 만들어주자. 즉, 호출만 적절히 잘 해주자.
def addRear(self, item): self.enqueue(item)
def deleteFront(self) : return self.dequeue()
def getFront(self): return self.peek()이제 덱에만 있는 기능들을 구현해보자. addFront와 deleteRear은 반대 방향 회전에만 신경을 써주면 된다. getRear은 현재 rear가 가리키는 항목을 반환하면 된다.
def addFront (self,item): #새로운 기능: 전단 삽입
if not self.isFull():
self.items[self.front] = item #항목 저장
self.front = self.front - 1 #반시계 방향으로 회전
if self.front < 0 : self.front = MAX_QSIZE -1
============================================================
def deleteREar(self):
if not self.isEmpty():
item = self.items[self.rear]; #항목 복사
self.rear = self.rear - 1 #반시계 방향으로 회전
if self.rear < 0 : self.rear = MAX_QSIZE - 1
return item #항목 반환
===========================================================
def getRear(self): #새로운 기능 : 후단 peek
return self.items[self.rear] 구현 끝! 이제 시간 복잡도를 생각해보자.
- 이름만 바뀌는 연산들은 이미 큐에서 모두 O(1)임을 확인
- getRear은 명백히 O(1)이다.
- 새로 추가한 addFront, 삭제연산 deleteRear도 항목의 이동은 없고 인덱스만 변경한다. 따라서 O(1)
5.6 우선순위 큐
자, 우리가 운전중이다. 근데 뒤에서 엠뷸런스나 소방차가 온다. 그러면 큐, 덱 이런 정렬이 아니라 무조건 '먼저 가세요!' 비켜줘야 한다. 그게 바로 우선순위 개념을 큐에 도입한 자료구조이다. 이는 모든 데이터가 우선순위를 가지고 있고, 들어온 순서와 상관 없이 우선순위가 높은 데이터가 먼저 출력된다. 이상해보이지만 가장 현실적이고 일반적인 큐이다.
시뮬레이션, 네트워크 트래픽, 운영체제의 작업스케쥴링 등에서 사용 중!우선순위 큐 추상 자료형
삭제연산에서 어떤 요소가 먼저 삭제되는가에 따라서 최대 우선순위 큐, 최소우선순위 큐로 나뉜다. 그러나 대부분 우선순위 큐는 가장 높은 우선순위 요소가 먼저 삭제되는 최대 우선순위 큐를 의미.