영어 단어 "Heap"의 뜻은 "무엇인가 차곡차곡 쌓아올린 더미"라는 뜻이다.
자료구조 힙(heap) 이란?
자료구조 힙(Heap)이란, 최댓값 또는 최솟값을 빠르게 찾기 위해 고안된 자료구조이다. 완전 이진 트리를 기반으로 한다.
힙의 특징은 다음과 같다.
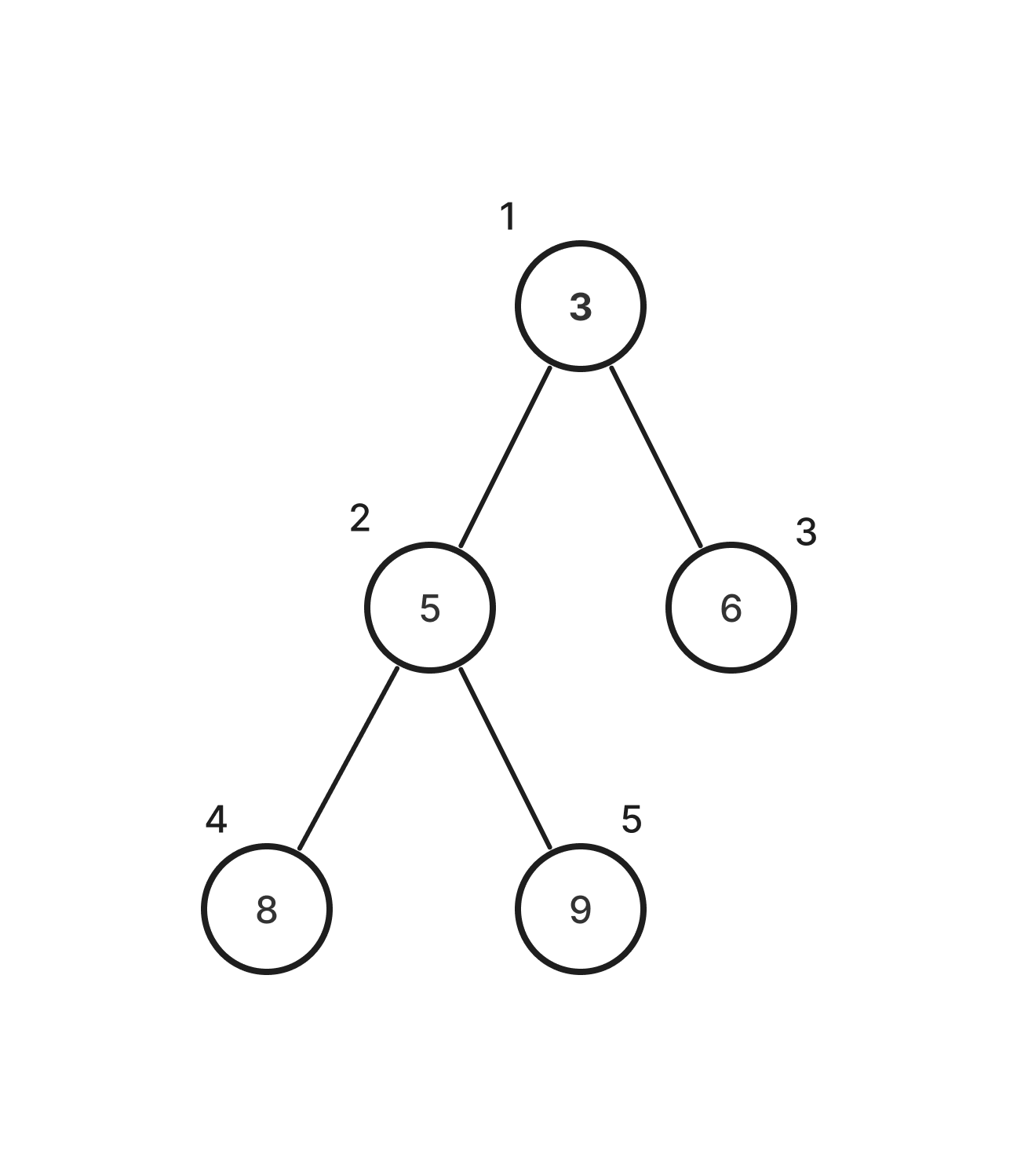
✅ 완전 이진 트리 형태로 배열을 사용(중요)하여 효율적으로 동작한다.
✅ 최대 또는 최소값이 항상 루트에 있다.
✅ 우선순위 큐와 같은 상황에서 사용된다.
우선순위 큐(Priority Queue)
일반적인 큐(Queue)는 선입선출(FIFO)인 반면, 우선순위 큐는 우선순위가 높은 원소들이 먼저 처리된다. 따라서 힙은 우선순위 큐를 구현하기 위한 자료구조 중 하나이다.
우선순위 큐는 추상적 자료구조로, 이를 구현하는 방법 중 가장 효율적인게 힙이라고 생각한다.
리스트로 구현하기
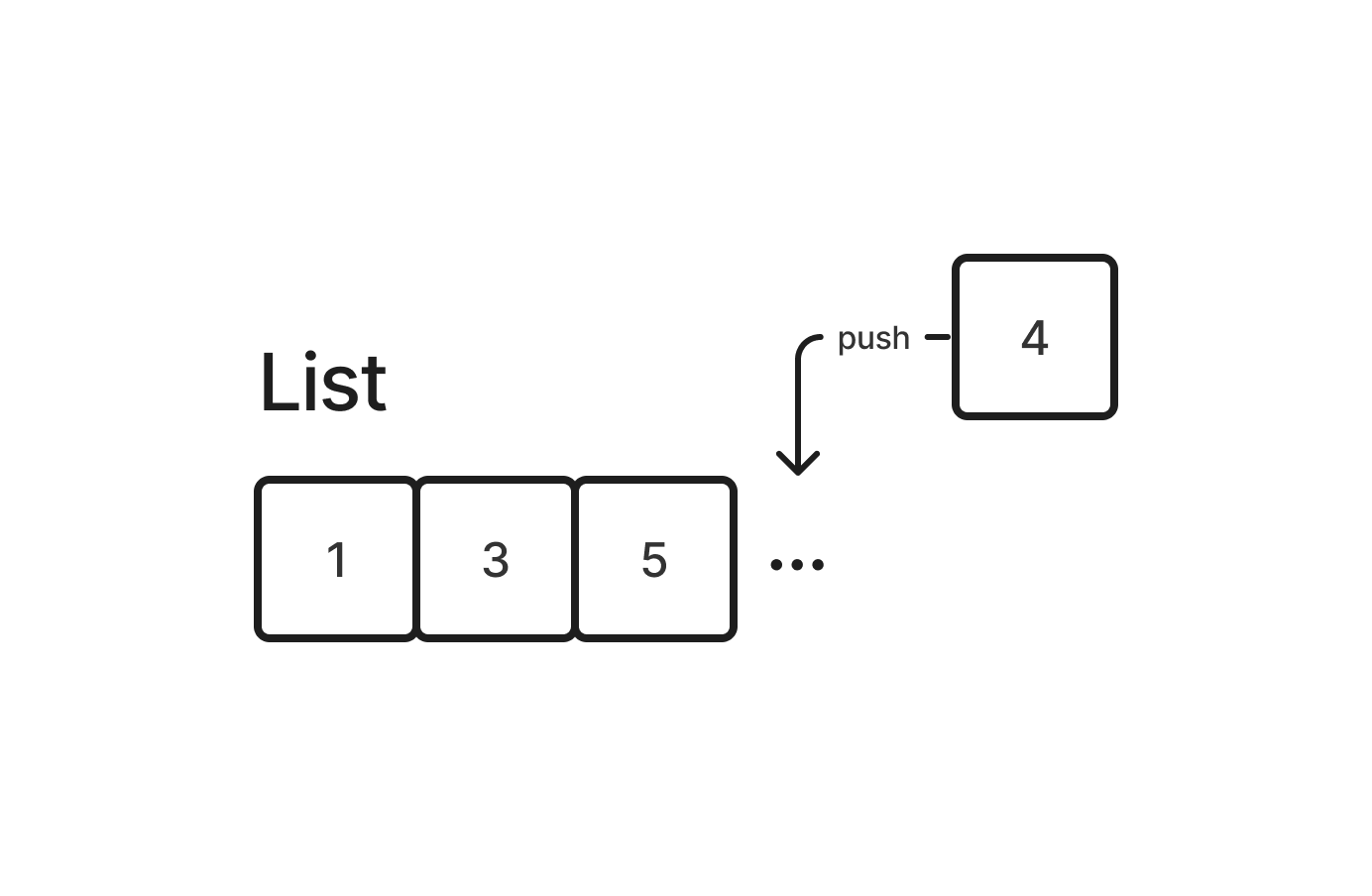
배열과 같은 선형 자료구조로도 우선순위 큐를 구현할 수 있다. 단, 선형 자료구조 특성상 삽입 또는 삭제가 O(n)의 시간복잡도를 가진다.
| 구현 | 삽입 | 루트 삭제 |
|---|---|---|
| 정렬되지 않은 배열 | O(1) | O(n) |
| 정렬된 배열 | O(n) | O(1) |
삭제 연산은 보통 최대/최소값을 담고있는 루트 노드의 삭제를 말한다.
힙으로 구현하기
배열로 구현된 우선순위 큐는 삭제 연산과 정렬에 대한 효율성이 떨어진다. 이러한 단점을 극복하기 위해 힙은 구조적 특성상 삽입 및 삭제 연산의 효율성을 유지할 수 있다.
- 힙의 삽입 연산
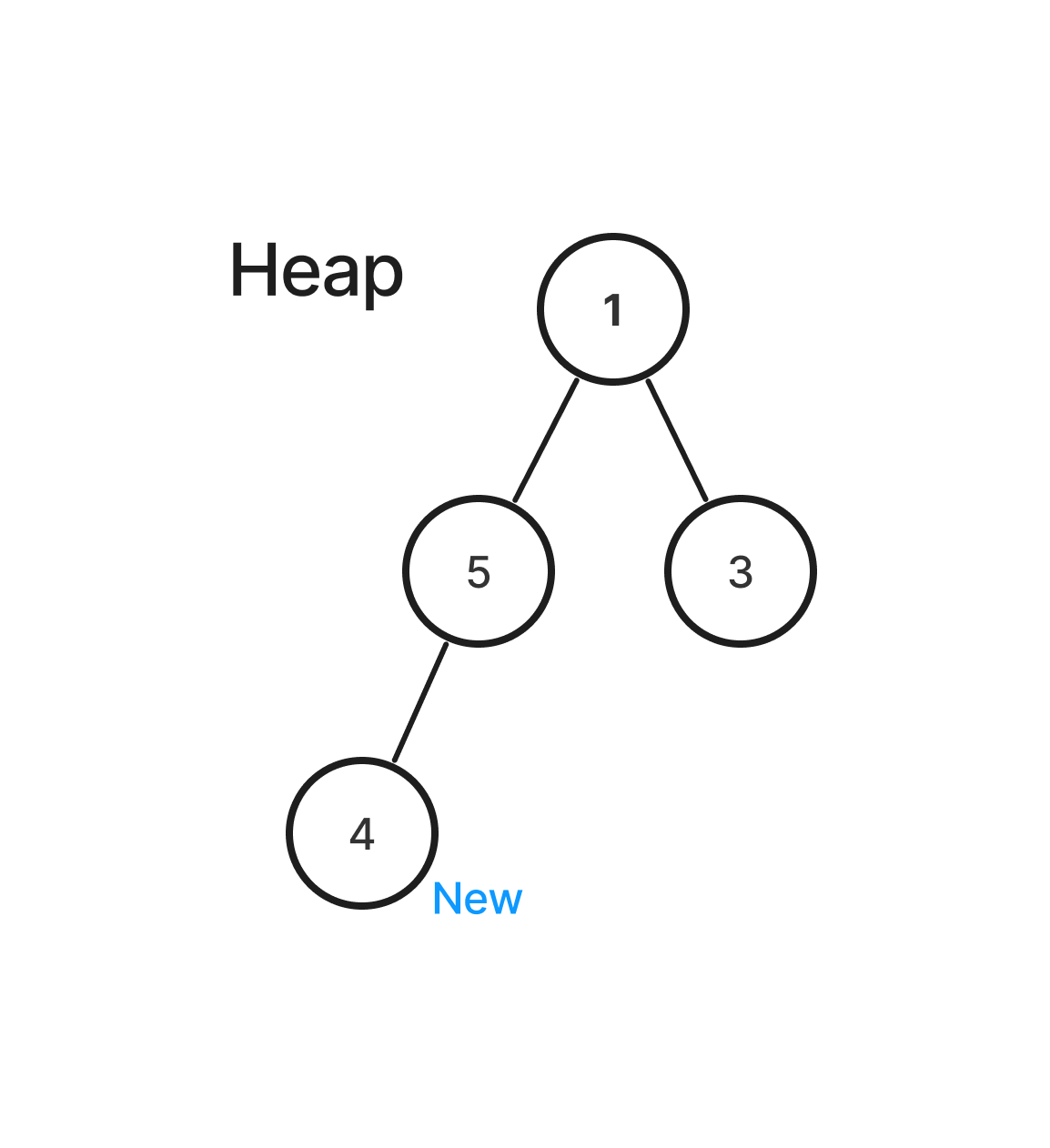
- 힙은 완전 이진 트리로 구성되어 있으므로 새로운 요소를 마지막 레벨에 추가한다.
- 새로운 요소는 부모 노드와 비교하여 조건이(부모 노드보다 값이 크거나 또는 작거나) 성립되었을 경우, 부모 노드와 위치를 조정한다.
- 이 과정에서 최악의 경우는 루트 노드까지 조정이 이루어지는 것이다. 따라서 시간복잡도는
O(log n)이다.
- 힙의 삭제 연산
- 루트 노드가 삭제됨에 따라 힙의 특성을 유지하기 위해 마지막 노드를 루트로 이동시키고, 다시 힙의 특성을 만족할 때까지 조정이 이루어진다.(이를 heapify라고 부름)
힙의 종류
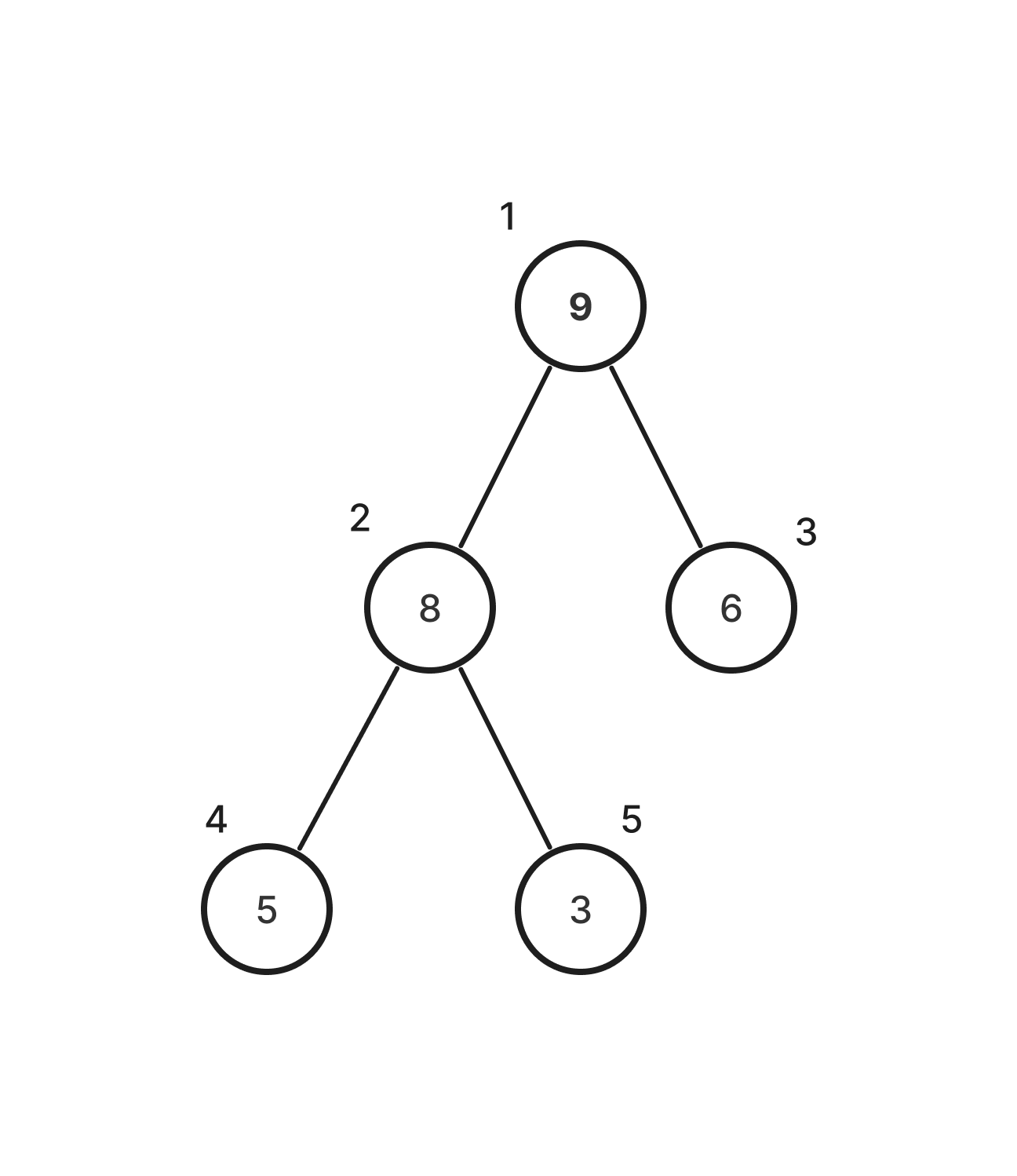
힙은 최대 힙(Max-Heap)과 최소 힙(Min-Heap), 이렇게 두 가지 유형이 있다.
최대 힙(Max-Heap)
루트 노드의 값은 모든 하위 노드 중 가장 커야 하며, 하위 트리에도 동일하게 구성된다.
최소 힙(Min-Heap)
루트 노드의 값은 모든 하위 노드 중 가장 작아야 하며, 하위 트리에도 동일하게 구성된다.
힙 동작원리
힙은 특성상 최소(또는 최대) 값이 루트이며 부모 노드가 자식 노드보다 작거나 크다. 이러한 특성을 유지하기 위해 새로운 값이 들어올 경우 이진 트리의 가장 마지막 노드에 추가되며, 부모 노드와 값을 비교하여 조건을 만족할 때까지 위치를 이동한다.
편의를 위해 이제부터 최소 힙을 예시로 설명하겠다.
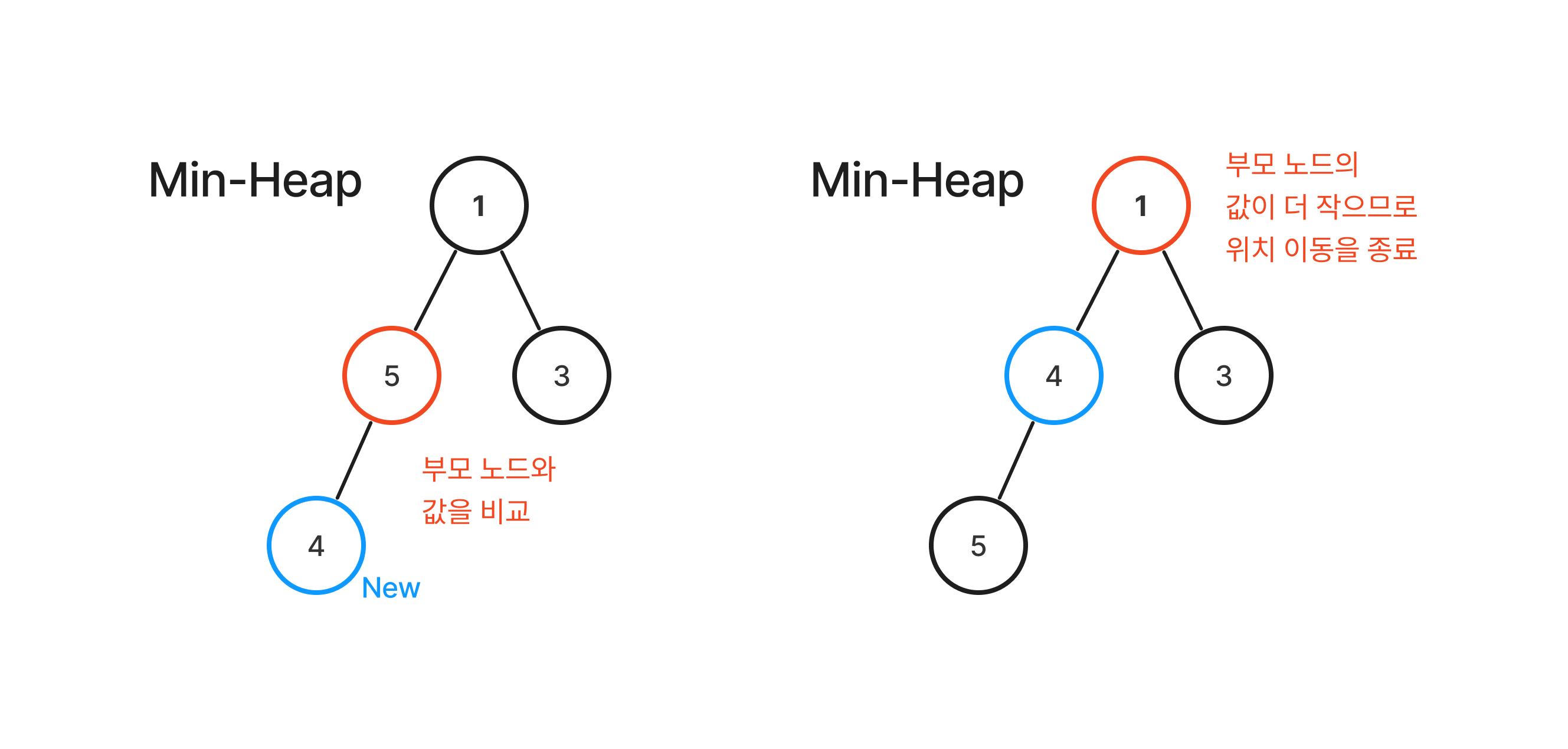
삽입(Insert)
새로운 요소는 트리의 마지막 레벨에 추가한다. 이후 부모 노드보다 값이 더 작을 경우 위치를 이동하며 순회한다. 이러한 과정을 통해 힙의 특성을 유지한다.
완전 이진 트리의 특성상 값은 왼쪽 아래부터 채워진다.
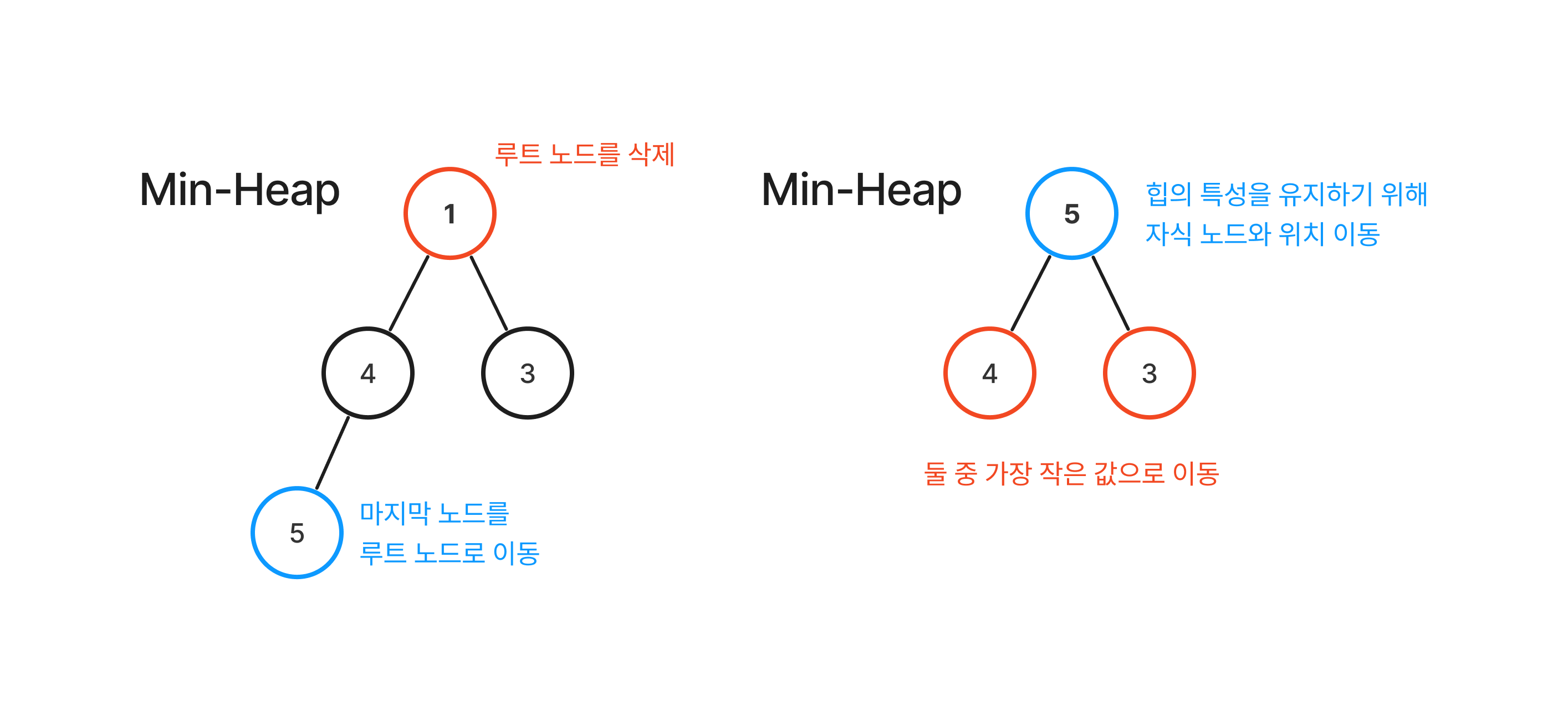
삭제(pop)
삭제는 보통 최소 값을 담고 있는 루트 노드의 삭제를 의미한다. 루트 노드가 삭제되면 마지막 레벨에 있는 노드를 루트 노드로 이동시킨다. 이후 힙의 특성을 유지하기 위해 자식 노드와 값을 비교하며 이동 및 순회하며 재정렬 한다.
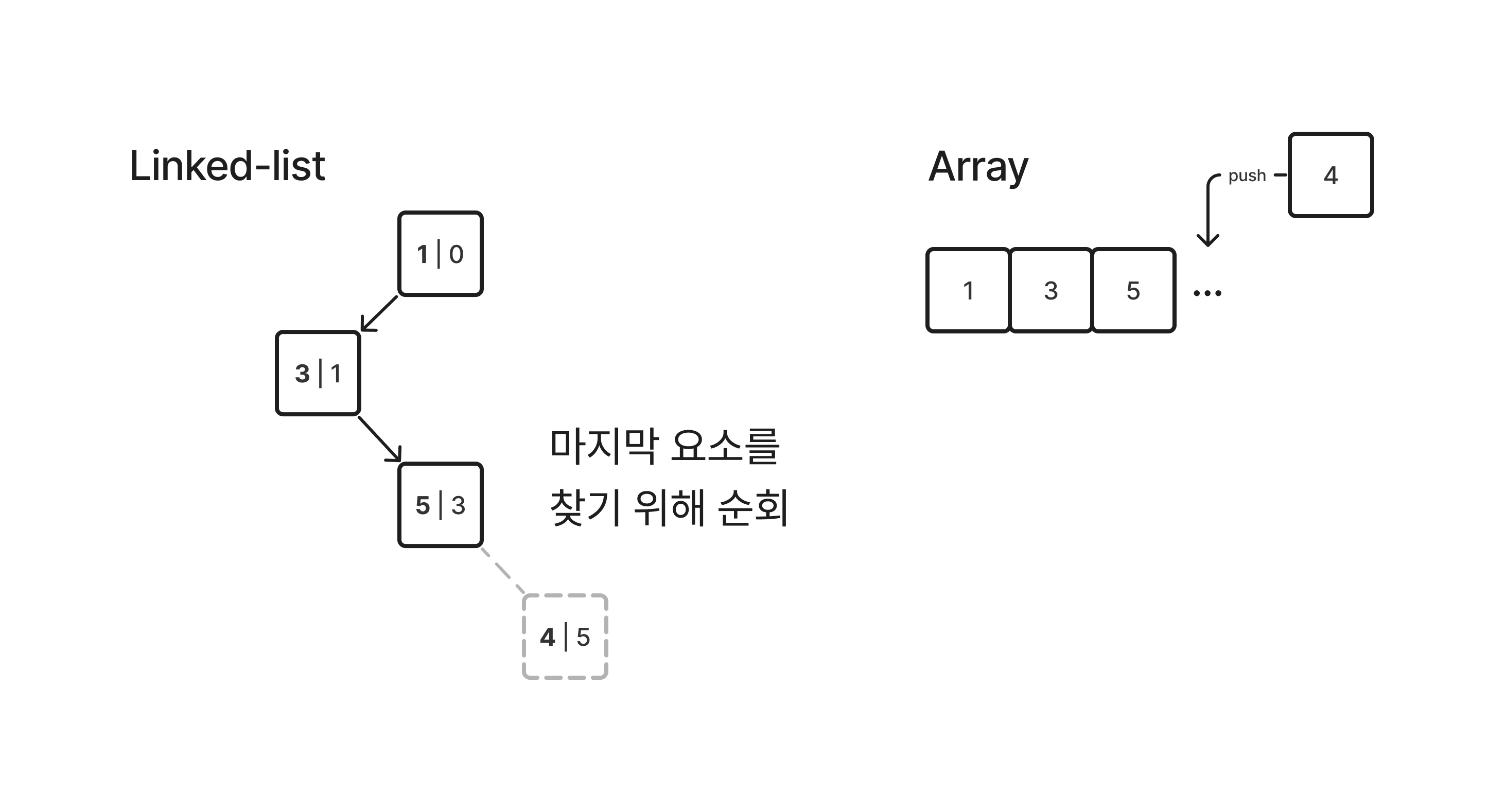
힙을 배열로 구현해야 하는 이유
힙은 기본적으로 배열로 구현해야 한다. 하지만 트리 형태의 힙을 Linked-list로 구현하지 않는 이유는 삽입과 삭제 의 마지막 요소 때문에 그렇다.
| 자료구조 | 설명 |
|---|---|
| 배열 | 삽입 및 삭제에 따라 마지막 요소를 찾기가 쉬움 |
| 링크드 리스트 | 삽입 및 삭제에 따라 마지막 요소를 찾기 위해 리스트를 순회한다. 따라서 배열보다 비효율적 |