[Silver III] 1로 만들기 - 1463

문제 링크

나의 풀이

import sys
input = sys.stdin.readline
n = int(input())
dp = [0] * 1000001
for i in range(2, n+1):
    dp[i] = dp[i-1] +1
    if i%2 == 0:
        dp[i] = min(dp[i], dp[i//2]+1)
    if i%3 == 0:
        dp[i] = min(dp[i], dp[i//3]+1)
print(dp[n])

1로 만들기 위한 최소 연산 횟수를 계산하는 다이나믹 프로그래밍(DP) 방식이다.
dp[i]는 정수 𝑖를 1로 만들기 위한 최소 연산 횟수를 저장하는 배열이다.
초기화
dp[1] = 0 (이미 1이므로 연산이 필요 없음), dp[2], dp[3]부터 계산
점화식
각 정수𝑖에 대해 최소 연산 횟수는 3가지 연산 중 최솟값을 선택한 결과다.

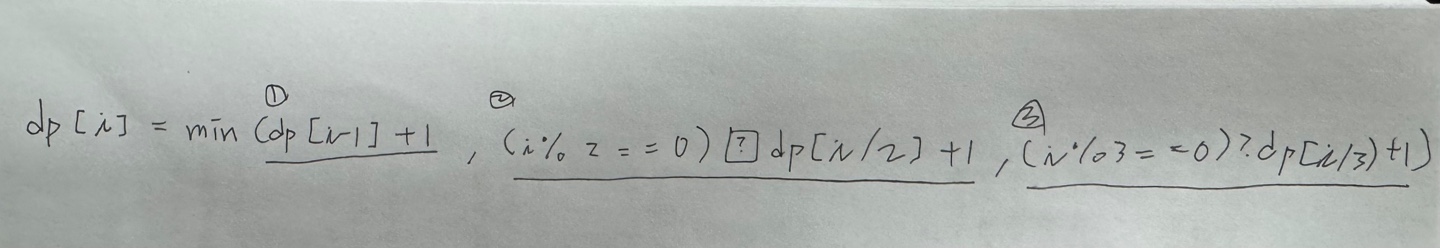
dp[i-1] + 1: 1을 빼는 연산
dp[i//2] + 1: 2로 나누어 떨어지면 2로 나누는 연산
dp[i//3] + 1: 3으로 나누어 떨어지면 3으로 나누는 연산

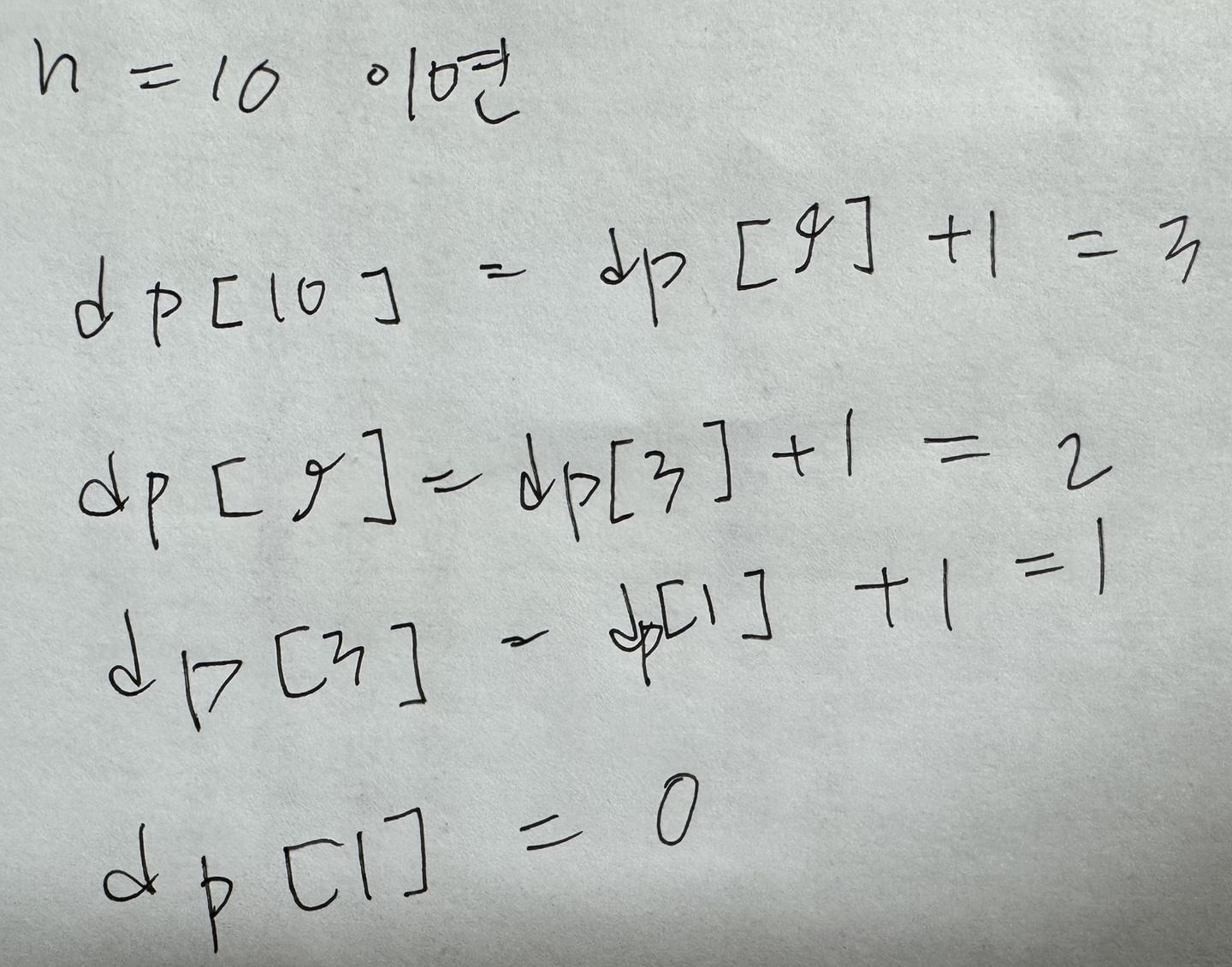
성능 요약

메모리: 40224 KB, 시간: 484 ms

분류

다이나믹 프로그래밍

제출 일자

2025년 1월 12일 18:23:38

문제 설명

정수 X에 사용할 수 있는 연산은 다음과 같이 세 가지 이다.

1. X가 3으로 나누어 떨어지면, 3으로 나눈다.
2. X가 2로 나누어 떨어지면, 2로 나눈다.
3. 1을 뺀다.

정수 N이 주어졌을 때, 위와 같은 연산 세 개를 적절히 사용해서 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하시오.

입력

첫째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.

출력

첫째 줄에 연산을 하는 횟수의 최솟값을 출력한다.