동적계획법(Dynamic Programming)

DP, 다이나믹 프로그래밍(또는 동적 계획법)란?

DP, 즉 다이나믹 프로그래밍(또는 동적 계획법)은 복잡한 문제를 더 작은 하위 문제로 나누어 해결하는 알고리즘 설계 기법입니다.

🔎 알고리즘 설계 기법과 알고리즘 기법
1. 알고리즘 기법
문제를 해결하기 위해 사용되는 절차적인 방법 또는 계획
(EX, 정렬 알고리즘, 검색 알고리즘, 그래프 탐색 알고리즘 등)

2. 알고리즘 설계 기법
문제 해결을 위해 알고리즘을 설계하는 방법이나 접근 방식을 나타냅니다. 설계 기법은 알고리즘을 개발하고 구현하는 데 사용되는 전략이나 원칙들을 포함합니다.
(EX, 분할 정복, 동적 계획법, 탐욕적 알고리즘, 백트래킹 등)

---

DP과 재귀적 호출의 차이점은 무엇일까? 🧐

1. 하향식(Top-down) vs 상향식(Bottom-up) 접근

재귀적 호출은 주로 하향식(top-down) 접근 방식을 사용합니다. 즉, 큰 문제를 작은 하위 문제로 나누어 해결하는 방식입니다. 반면에 동적 계획법은 주로 상향식(bottom-up) 접근 방식을 사용합니다. 작은 하위 문제들부터 시작하여 그 결과를 저장하고, 이를 이용하여 점진적으로 큰 문제의 해를 구해나갑니다.

메모이제이션(Memoization)

동적 계획법은 중복되는 계산 결과를 저장하는 메모리 기법인 메모이제이션을 사용합니다. 이를 통해 이전에 계산한 값을 캐시하고, 다시 필요할 때 해당 값을 가져와 재사용합니다. 이는 재귀적 호출에서의 중복 계산을 방지하고 계산 속도를 향상시킵니다.

---

DP 기법을 적용시킬 수 있는 조건

1. 중복되는 부분 문제(Overlapping Subproblems)

DP는 기본적으로 문제를 나누고 그 문제의 결과 값을 재활용해서 전체 답을 구한다. 그래서 동일한 작은 문제들이 반복하여 나타나는 경우에 사용이 가능합니다.

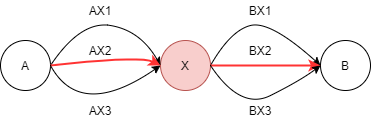
2. 최적 부분 구조(Optimal Substructure)

부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과를 낼 수 있는 경우 사용이 가능합니다.

A - B까지의 가장 짧은 경로를 찾고자 하는 경우를 예시로 할 때, 중간에 X가 있을 때, A - X / X - B(부분 문제의 최적 결과)가 많은 경로 중 가장 짧은 경로라면 전체 최적 경로도 A - X - B(전체 문제의 최적 결과)가 정답이 된다.

---

DP로 문제 푸는 방법

방법은 아래와 같습니다.

1. 📝 메모하기
   변수 값에 따른 결과를 저장할 배열 등을 미리 만들고 그 결과를 나올 때마다 배열 내에 저장하고 그 저장된 값을 재사용하는 방식으로 문제를 해결해 나간다.
2. 🧮 변수 간 관계식(점화식) 만들기
   예를 들어 피보나치 수열의 f(n) = f(n-1) + f(n-2) 라는 식

DP 문제 해결 방식은 크게 두가지가 있습니다.

1. Bottom-Up (Tabulation 방식) - 반복문 사용
   Bottom-Up 방식은 작은 부분 문제부터 차례대로 해결하여 전체 문제를 해결하는 방식입니다. 이를 위해 반복문을 사용하여 반복적으로 부분 문제들을 해결하고, 결과를 배열 등에 저장합니다.

   👍 일반적으로 더 직관적이고 이해하기 쉽습니다. 또한, 모든 작은 부분 문제를 해결하므로 최적 부분 구조를 보장합니다.

2. Top-Down (Memoization 방식) - 재귀 사용
   큰 문제를 작은 부분 문제로 나누어 해결하는 방식입니다. 이를 위해 재귀 함수를 사용하여 문제를 작은 부분 문제들로 쪼개고, 중복 계산을 피하기 위해 이전에 계산한 값을 저장하는 Memoization을 활용합니다. Memoization은 캐싱을 통해 이전 계산 결과를 저장하여 중복 계산을 피하는 것을 의미합니다.

   👍 Memoization은 재귀를 사용하므로 구현이 더 간단할 수 있습니다. 또한, 필요한 부분 문제만 해결하므로 계산 시간을 절약할 수 있습니다. 하지만 재귀 호출의 오버헤드가 발생할 수 있으며, 모든 작은 부분 문제를 해결하지 않을 경우 최적 부분 구조를 보장하지 않을 수 있습니다

---

대표적인 DP 문제들

DP는 다양한 문제에서 사용될 수 있습니다. 위의 2가지 조건을 참고하여 DP로 해결할 수 있는 문제인지 파악할 수 있습니다. 보통 특정 데이터 내 최대화 / 최소화 계산을 하거나 특정 조건 내 데이터를 세야 한다거나 확률 등의 계산의 경우 DP로 풀 수 있는 경우가 많습니다.

1.피보나치 수열 > Top-Down 방식

피보나치 수열은 이전 두 항의 합으로 이루어지는 수열입니다. 동적 계획법을 사용하여 피보나치 수열을 구할 수 있습니다. 작은 문제부터 시작하여 계산 결과를 저장하고 이를 이용하여 큰 문제의 해를 구합니다.

function fibonacci(n) {
  // 🌟 메모이제이션 🌟
  // 피보나치 수열을 저장할 배열
  const dp = new Array(n + 1);

  // 초기값 설정
  dp[0] = 0;
  dp[1] = 1;

  // 🌟 점화식 🌟
  // 피보나치 수열 계산
  for (let i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }

  // 결과 반환
  return dp[n];
}

// 예시로 n = 10일 때 피보나치 수열 값 출력
console.log(fibonacci(10));  // Output: 55

2. 배낭 문제(Knapsack Problem) > Bottom-Up 방식

주어진 가방의 용량에 최대한 가치가 높은 물건을 넣는 문제입니다. 각 물건은 가치와 무게를 가지고 있으며, 동적 계획법을 사용하여 가방의 용량에 따른 최대 가치를 구할 수 있습니다.

function knapsack(weights, values, capacity) {
  const n = weights.length;

  // 🌟 메모이제이션 🌟
  // 동적 계획법을 위한 2차원 배열 초기화
  const dp = new Array(n + 1);
  for (let i = 0; i <= n; i++) {
    dp[i] = new Array(capacity + 1).fill(0);
  }

  // 🌟 점화식 🌟
  // 배낭 문제 해결
  for (let i = 1; i <= n; i++) {
    for (let j = 1; j <= capacity; j++) {
      if (weights[i - 1] > j) {
        // 현재 아이템을 배낭에 넣을 수 없는 경우
        dp[i][j] = dp[i - 1][j];
      } else {
        // 현재 아이템을 배낭에 넣을 수 있는 경우
        dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1]);
      }
    }
  }

  // 결과 반환
  return dp[n][capacity];
}

// 예시로 아이템의 무게와 가치, 배낭의 용량이 주어졌을 때 최대 가치 출력
const weights = [2, 3, 4, 5];
const values = [3, 4, 5, 6];
const capacity = 7;

console.log(knapsack(weights, values, capacity));  // Output: 9

3. 최장 증가 부분 수열(Longest Increasing Subsequence) > Bottom-Up 방식

주어진 수열에서 순서를 유지하면서 가장 긴 부분 수열을 찾는 문제입니다. 동적 계획법을 사용하여 각 원소를 마지막으로 하는 부분 수열의 길이를 저장하고, 이를 이용하여 전체 최장 증가 부분 수열의 길이를 구할 수 있습니다.

function longestIncreasingSubsequence(nums) {
  const n = nums.length;

  // 🌟 메모이제이션 🌟
  // 동적 계획법을 위한 배열 초기화
  const dp = new Array(n).fill(1);

  // 🌟 점화식 🌟
  // 최장 증가 부분 수열 계산
  for (let i = 1; i < n; i++) {
    for (let j = 0; j < i; j++) {
      if (nums[i] > nums[j]) {
        dp[i] = Math.max(dp[i], dp[j] + 1);
      }
    }
  }

  // 결과 중 최대값 반환
  return Math.max(...dp);
}

// 예시로 배열 [10, 9, 2, 5, 3, 7, 101, 18]의 최장 증가 부분 수열의 길이 출력
const nums = [10, 9, 2, 5, 3, 7, 101, 18];

console.log(longestIncreasingSubsequence(nums));  // Output: 4

4. 최단 경로 문제(Shortest Path Problem) > Bottom-Up 방식

주어진 그래프에서 시작 노드부터 도착 노드까지의 최단 경로를 찾는 문제입니다. 동적 계획법을 사용하여 각 노드까지의 최단 거리를 저장하고, 이를 이용하여 최단 경로를 찾을 수 있습니다.

function shortestPath(graph, start, end) {
  const n = graph.length;
  // 🌟 메모이제이션 🌟
  const dp = new Array(n).fill(Infinity);
  dp[start] = 0;

  // 🌟 점화식 🌟
  for (let i = start; i <= end; i++) {
    for (let j = 0; j < n; j++) {
      if (graph[i][j] !== 0 && dp[i] + graph[i][j] < dp[j]) {
        dp[j] = dp[i] + graph[i][j];
      }
    }
  }

  return dp[end];
}

// 예시로 그래프와 시작점, 도착점이 주어졌을 때 최단 경로의 길이 출력
const graph = [
  [0, 4, 2, 0],
  [4, 0, 1, 5],
  [2, 1, 0, 8],
  [0, 5, 8, 0]
];
const start = 0;
const end = 3;

console.log(shortestPath(graph, start, end));  // Output: 6

5. 문자열 편집 거리 문제(Edit Distance Problem) > Bottom-Up 방식

두 문자열 사이의 최소 편집 거리를 찾는 문제입니다. 편집 연산은 문자 삽입, 삭제, 대체 등이 있으며, 동적 계획법을 사용하여 각 문자열의 부분 문자열까지의 최소 편집 거리를 저장하고, 이를 이용하여 전체 편집 거리를 구할 수 있습니다.

function editDistance(str1, str2) {
  const m = str1.length;
  const n = str2.length;
  // 🌟 메모이제이션 🌟
  const dp = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));

  // 🌟 점화식 🌟
  for (let i = 0; i <= m; i++) {
    for (let j = 0; j <= n; j++) {
      if (i === 0) {
        dp[i][j] = j;
      } else if (j === 0) {
        dp[i][j] = i;
      } else if (str1[i - 1] === str2[j - 1]) {
        dp[i][j] = dp[i - 1][j - 1];
      } else {
        dp[i][j] = 1 + Math.min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]);
      }
    }
  }

  return dp[m][n];
}

// 예시로 두 문자열이 주어졌을 때 문자열 편집 거리 출력
const str1 = "kitten";
const str2 = "sitting";

console.log(editDistance(str1, str2));  // Output: 3

---

DP 장단점

장점

• 중복 계산을 줄일 수 있습니다.
• 효율적인 시간 복잡도를 가질 수 있스빈다.

단점

• 메모리 사용량이 큽니다. DP는 중간 결과를 저장하기 위해 추가적인 메모리를 사용합니다. 따라서 문제의 크기가 커질수록 필요한 메모리도 증가할 수 있습니다.

---

프로그래머스 문제들

• 정수 삼각형
• 등굣길
• 도둑질
• N으로 표현

---

참고 링크1