DFS, BFS 알고리즘 이해하고 문제 풀어보기! (+ 둘의 차이점)

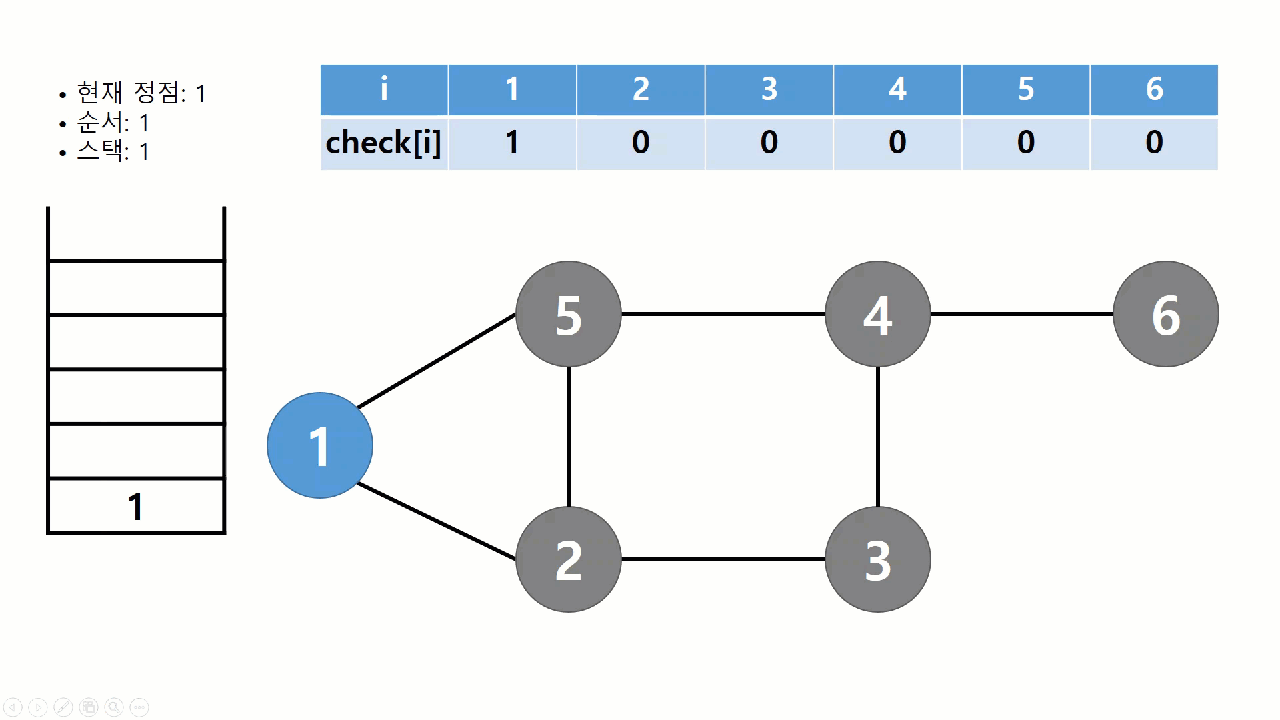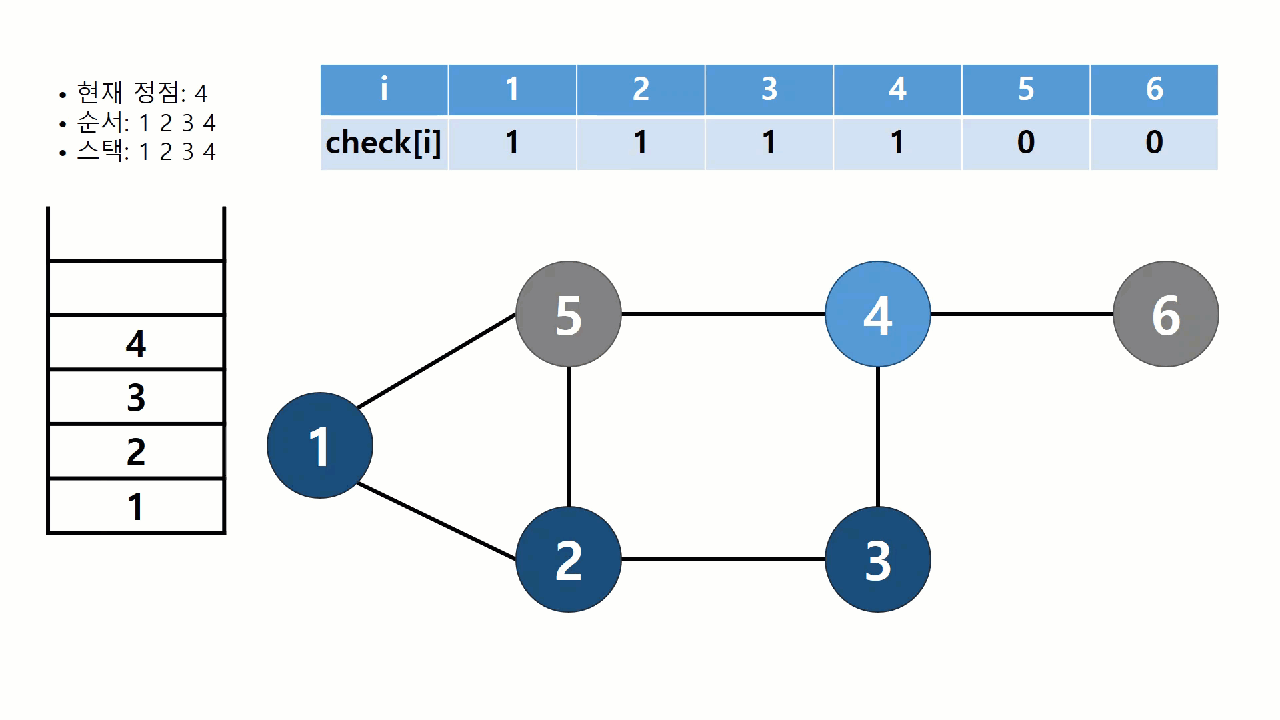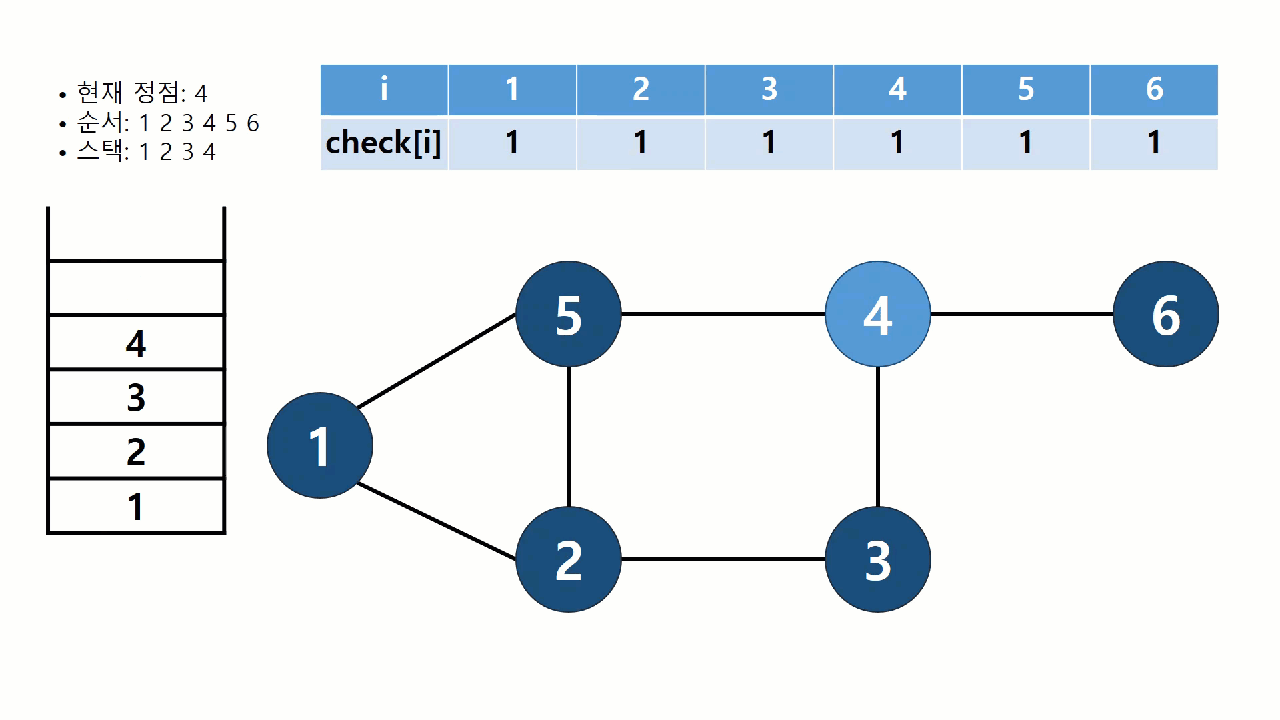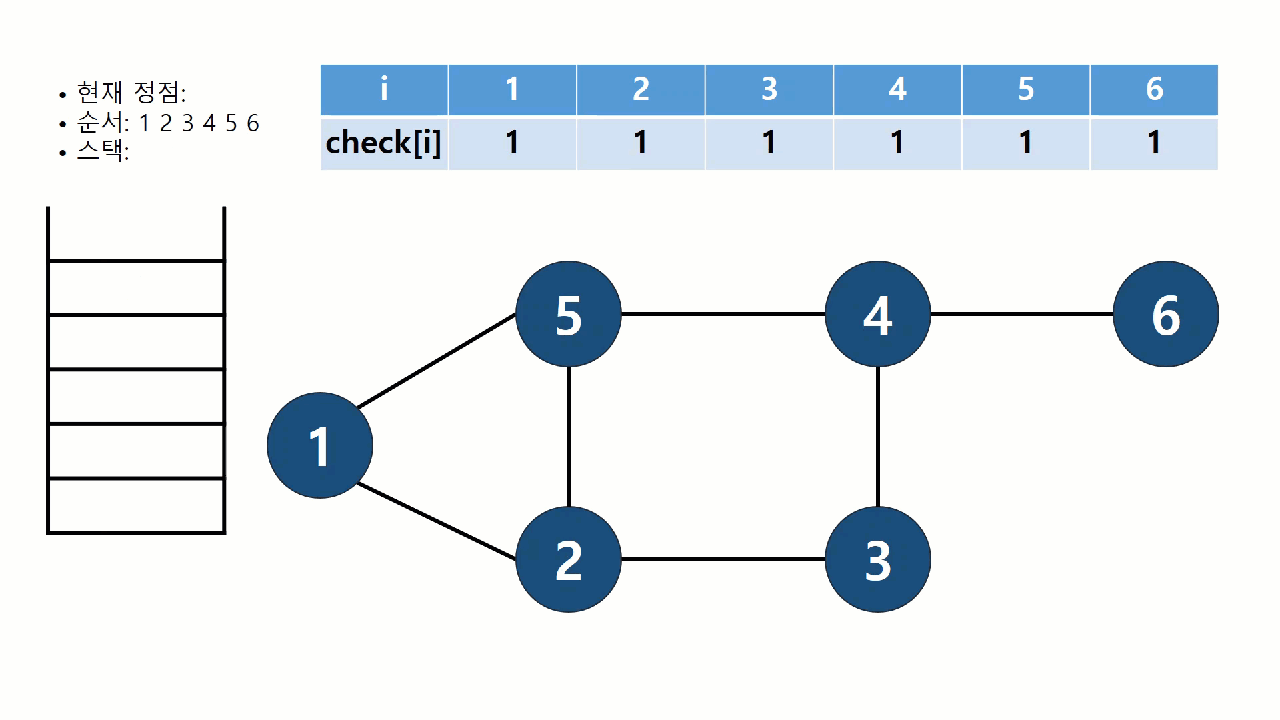
DFS 알고리즘

DFS란 깊이 우선 탐색 알고리즘을 말한다.

https://velog.io/@polynomeer/%EA%B9%8A%EC%9D%B4-%EC%9A%B0%EC%84%A0-%ED%83%90%EC%83%89DFS

---

DFS

1. DFS 그래프 스택, 큐, 재귀

1-1. DFS 그래프 스택

//스택
function dfsUsingStack(graph, start) {
  let stack = [start];
  let visited = new Set();

  while (stack.length > 0) {
    let node = stack.pop();
    if (!visited.has(node)) {
      console.log(node);
      visited.add(node);

      // 인접한 미방문 노드를 스택에 추가
      for (let neighbor of graph[node]) {
        if (!visited.has(neighbor)) {
          stack.push(neighbor);
        }
      }
    }
  }
}

// 그래프 예제
const graph = {
  A: ["B", "C"],
  B: ["A", "D", "E"],
  C: ["A", "F"],
  D: ["B"],
  E: ["B", "F"],
  F: ["C", "E"],
};

dfsUsingStack(graph, "A");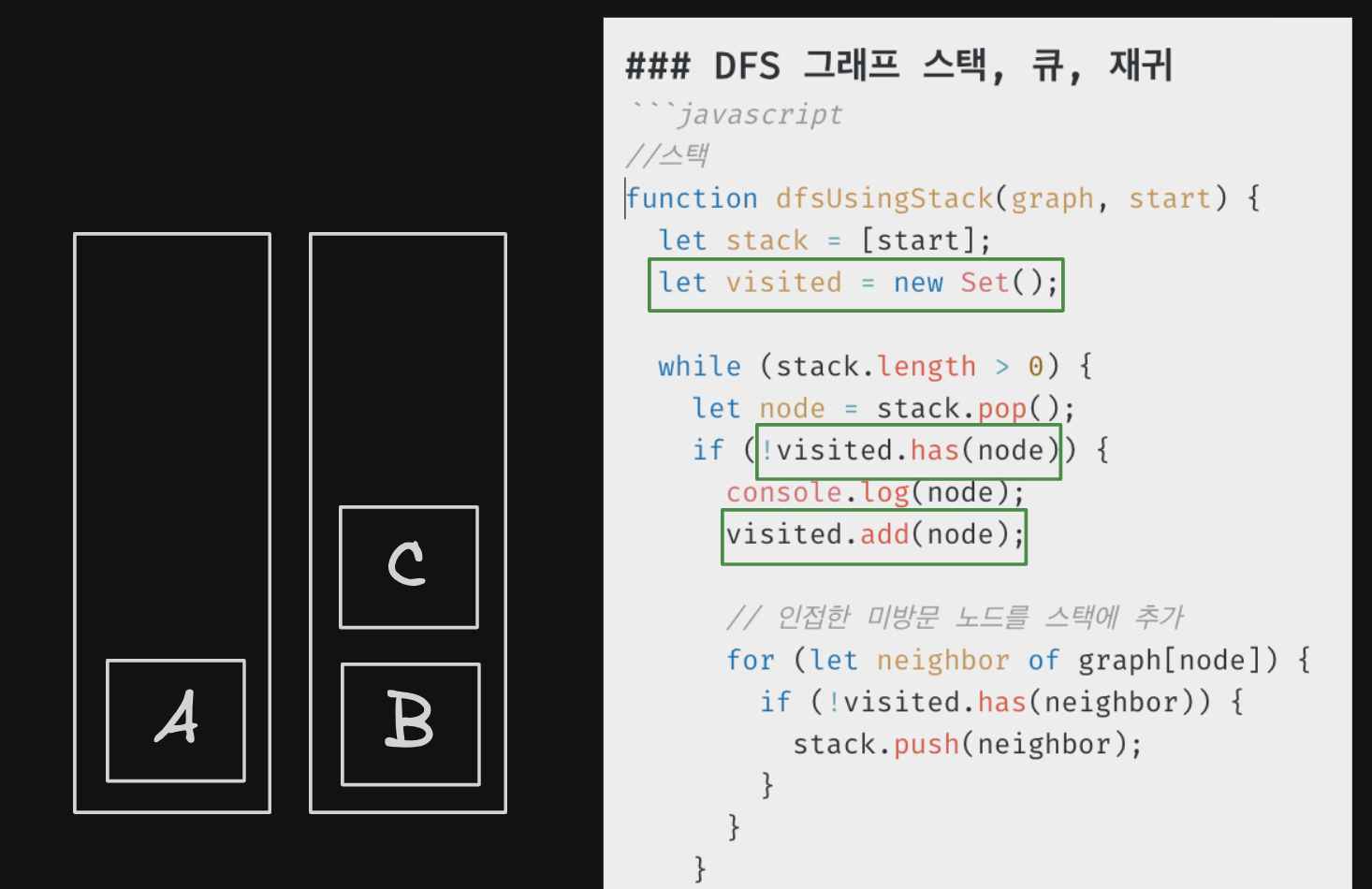

• Set 자료구조를 이용하여 visited를 결정
• has 함수를 통해 방문했는지 확인
• add를 통해 set 방문을 확인
• 이웃 노드를 계속해서 추가! (while stack.length > 0)

1-2. DFS 그래프 큐

//큐
function dfsUsingQueue(graph, start) {
  let queue = [start];
  let visited = new Set();

  while (queue.length > 0) {
    let node = queue.shift();
    if (!visited.has(node)) {
      console.log(node);
      visited.add(node);

      // 인접한 미방문 노드를 큐에 추가
      for (let neighbor of graph[node]) {
        if (!visited.has(neighbor)) {
          queue.push(neighbor);
        }
      }
    }
  }
}

// 위에서 정의한 그래프를 사용하여 호출
dfsUsingQueue(graph, "A");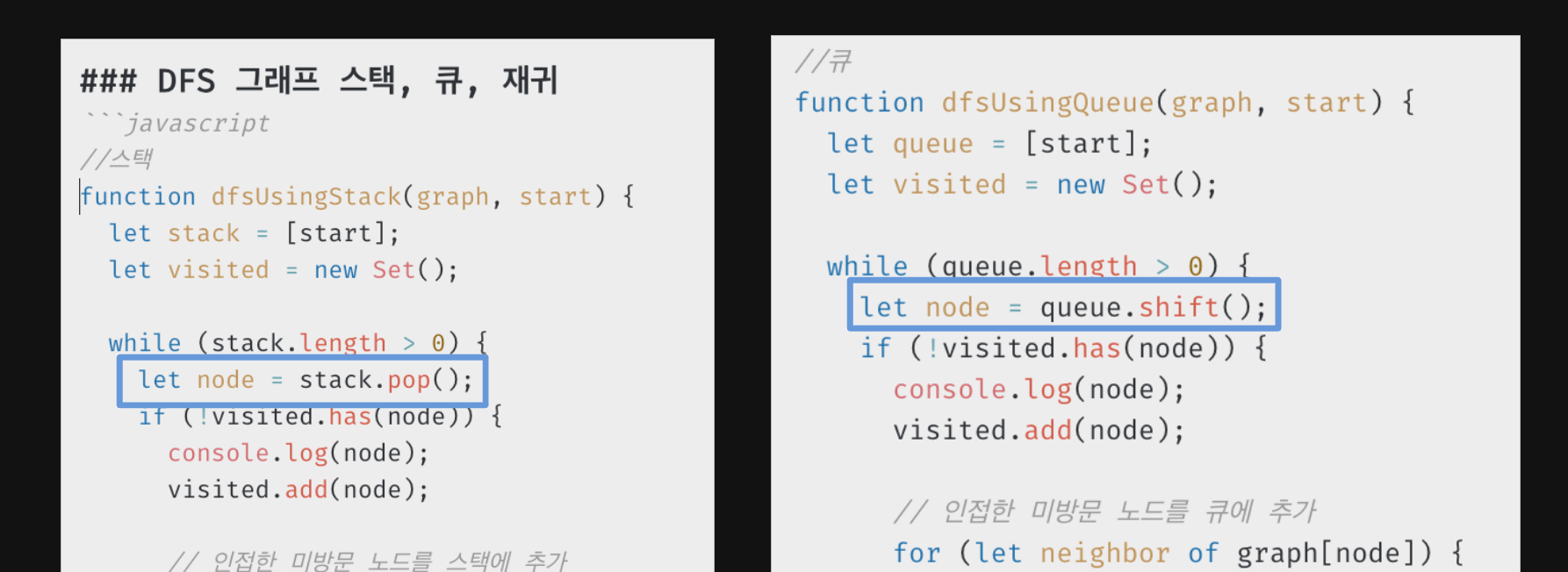

큐랑 스택은 pop인지 shift인지의 차이다

그래프의 오른쪽 부터 탐색하는지, 왼쪽에서부터 탐색하는지의 차이

1-3. DFS 그래프 큐

//재귀
function dfsRecursive(graph, node, visited) {
  if (!visited.has(node)) {
    console.log(node);
    visited.add(node);

    for (let neighbor of graph[node]) {
      if (!visited.has(neighbor)) {
        dfsRecursive(graph, neighbor, visited);
      }
    }
  }
}

// 위에서 정의한 그래프를 사용하여 호출
const visitedNodes = new Set();
dfsRecursive(graph, "A", visitedNodes);

재귀함수로 구현한 DFS는 재귀 호출마다 함수 호출 스택에 새로운 실행 컨텍스트(함수 자체)가 쌓입니다.

이로인한 단점은 무한 재귀에 빠지거나 그래프가 너무 클 경우 스택 메모리를 많이 소비하여 스택 오버플로우 문제를 발생 시킬 수 있습니다.

DFS 이차원 배열 스택, 큐, 재귀

//스택
function dfsUsingStack(graph, start) {
  let stack = [start];
  let visited = new Set();

  while (stack.length > 0) {
    let node = stack.pop();
    if (!visited.has(node)) {
      console.log(node);
      visited.add(node);

      // 인접한 미방문 노드를 스택에 추가
      for (let neighbor of graph[node]) {
        if (!visited.has(neighbor)) {
          stack.push(neighbor);
        }
      }
    }
  }
}

// 2D 배열로 그래프를 표현
const graph = [
  [1, 2],    // Node 0과 연결된 노드
  [0, 3, 4], // Node 1과 연결된 노드
  [0, 5],    // Node 2과 연결된 노드
  [1],       // Node 3과 연결된 노드
  [1],       // Node 4과 연결된 노드
  [2]        // Node 5과 연결된 노드
];

dfsUsingStack(graph, 0); // 시작 노드를 0으로 선택

//큐
function dfsUsingQueue(graph, start) {
  let queue = [start];
  let visited = new Set();

  while (queue.length > 0) {
    let node = queue.shift();
    if (!visited.has(node)) {
      console.log(node);
      visited.add(node);

      // 인접한 미방문 노드를 큐에 추가
      for (let neighbor of graph[node]) {
        if (!visited.has(neighbor)) {
          queue.push(neighbor);
        }
      }
    }
  }
}

// 2D 배열로 그래프를 표현
const graph = [
  [1, 2],    // Node 0과 연결된 노드
  [0, 3, 4], // Node 1과 연결된 노드
  [0, 5],    // Node 2과 연결된 노드
  [1],       // Node 3과 연결된 노드
  [1],       // Node 4과 연결된 노드
  [2]        // Node 5과 연결된 노드
];

dfsUsingQueue(graph, 0); // 시작 노드를 0으로 선택

//재귀
function dfsRecursive(graph, node, visited) {
  if (!visited.has(node)) {
    console.log(node);
    visited.add(node);

    for (let neighbor of graph[node]) {
      if (!visited.has(neighbor)) {
        dfsRecursive(graph, neighbor, visited);
      }
    }
  }
}

// 2D 배열로 그래프를 표현
const graph = [
  [1, 2],    // Node 0과 연결된 노드
  [0, 3, 4], // Node 1과 연결된 노드
  [0, 5],    // Node 2과 연결된 노드
  [1],       // Node 3과 연결된 노드
  [1],       // Node 4과 연결된 노드
  [2]        // Node 5과 연결된 노드
];

const visitedNodes = new Set();
dfsRecursive(graph, 0, visitedNodes); // 시작 노드를 0으로 선택

---

응용 문제 풀기! (2차원 배열로 DFS 구현하기)

📌 음료수 얼려 먹기

N * M 크기의 얼음 틀이 있다. 구멍이 뚫려 있는 부분은 0, 칸막이가 존재하는 부분은 1로 표시된다.
구멍이 뚫려 있는 부분끼리 상, 하, 좌, 우로 붙어있는 경우 서로 연결되어있는 것으로 간주한다.
이때 얼음 틀의 모양이 주어졌을 떄 생성되는 총 아이스크림의 개수를 구하는 프로그램을 작성하시오.
다음의 4 * 5 얼음틀 예시에서는 아이스크림이 총 3개 생성된다.

// 1. array만큼 visit을 만든후 false로 채운다.
// 2. array만큼 돌면서 
//     2-1. array의 값이 0이고
//     2-2. visit이 false라면
//     count ++ 해주고, dfs 호출

// 1. dfs에서 받은 값을 visit ture 해주고
// 2. 상하좌우로 검사한다. 만약 상하좌우에서
//     2-1. array 범위에 들어왔고
//     2-2. array의 값이 0이고
//     2-3. visit이 false라면
//     dfs 호출(count ++ 은 안해줌)

const directions = [[-1,0],[1,0],[0,1],[0,-1]];

const dfs = (curRow, curCol, array, visit) => {
    
    visit[curRow][curCol] = true;    

    for(let [dx, dy] of directions){
        const tempRow = dx + curRow;
        const tempCol = dy + curCol;
        

        if(tempRow >=0 && tempRow < array.length
           && tempCol >=0 && tempCol < array[0].length
           && array[tempRow][tempCol] === 0
           && visit[tempRow][tempCol] === false
          ){
            dfs(tempRow, tempCol, array, visit);
          }
    }
};

const solution = (row, col, arrayInput) => {
    const array = arrayInput.split('\n').map(row => row.split('').map(Number));
    const visit = new Array(row).fill(null).map(()=>new Array(col).fill(false));
    let count = 0;
    
    for(let x=0; x<array.length; x++){
        for(let y=0; y<array[0].length; y++){
            if(array[x][y] === 0 && visit[x][y] === false){
                count++;
                dfs(x, y, array, visit);
            }
        }
    }

    return count;
}

const input = `00000111100000
11111101111110
11011101101110
11011101100000
11011111111111
11011111111100
11000000011111
01111111111111
00000000011111
01111111111000
00011111111000
00000001111000
11111111110011
11100011111111
11100011111111`;



console.log(solution(15,14,input));

---

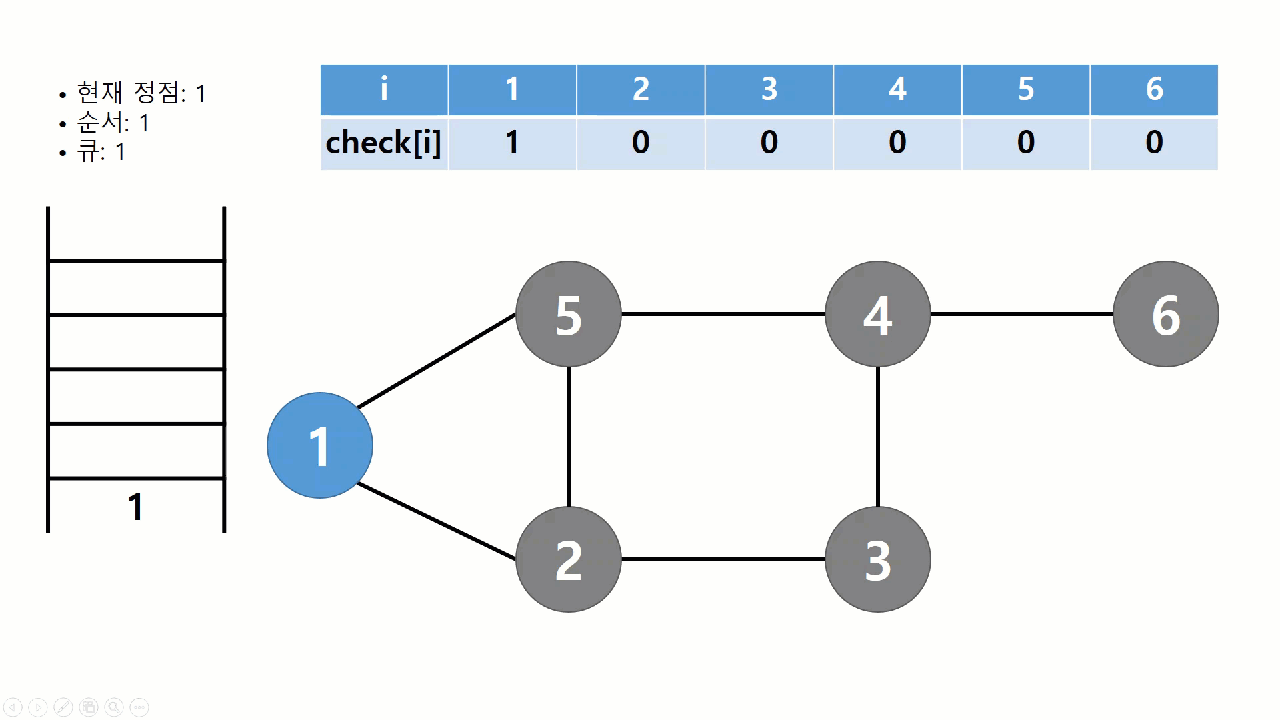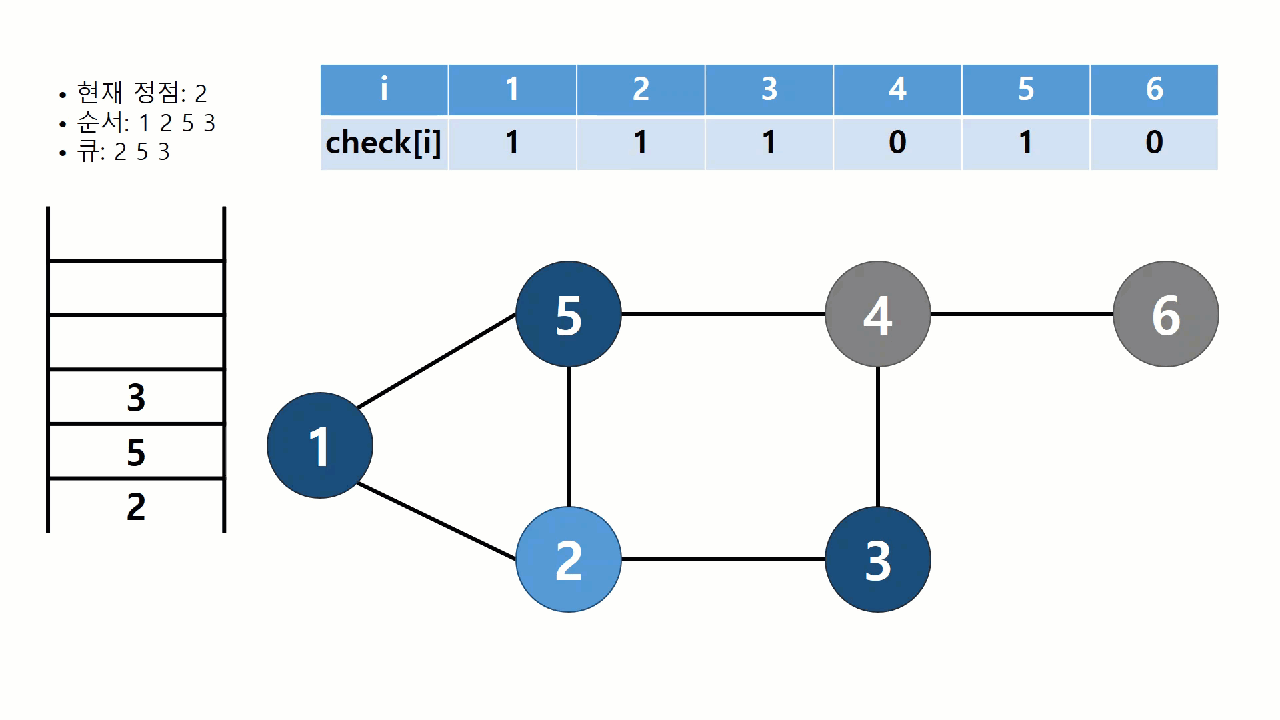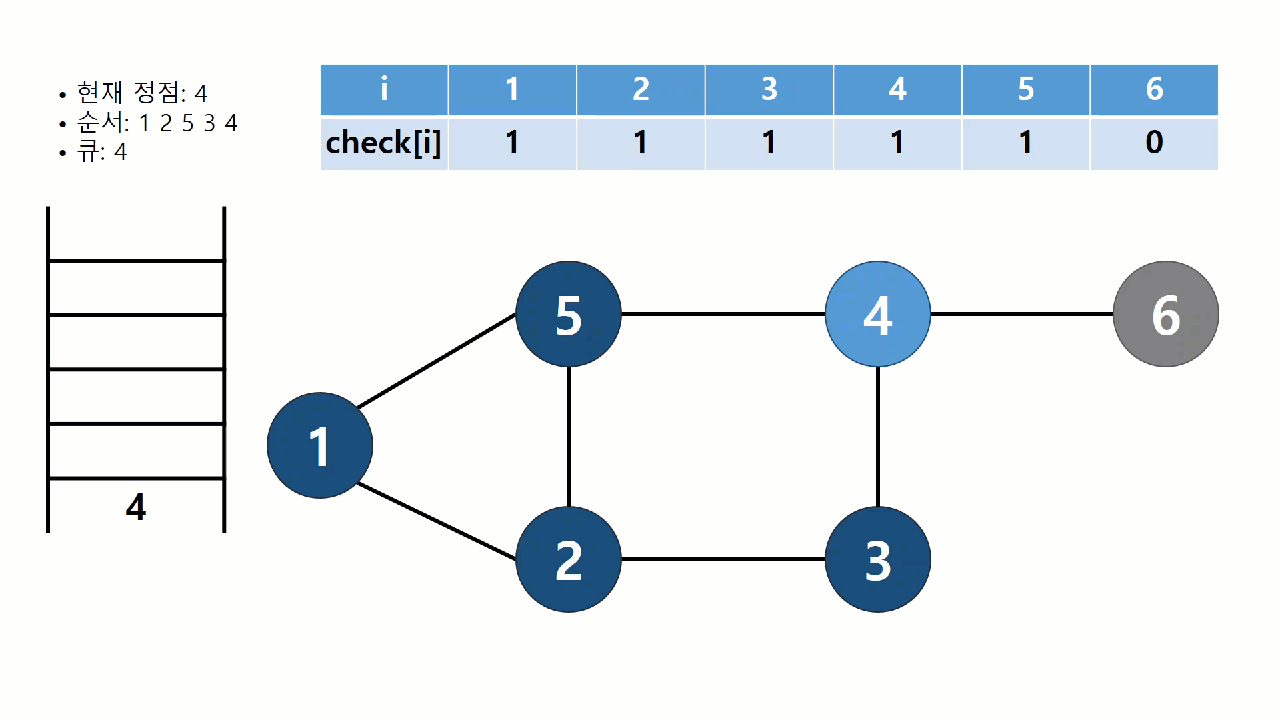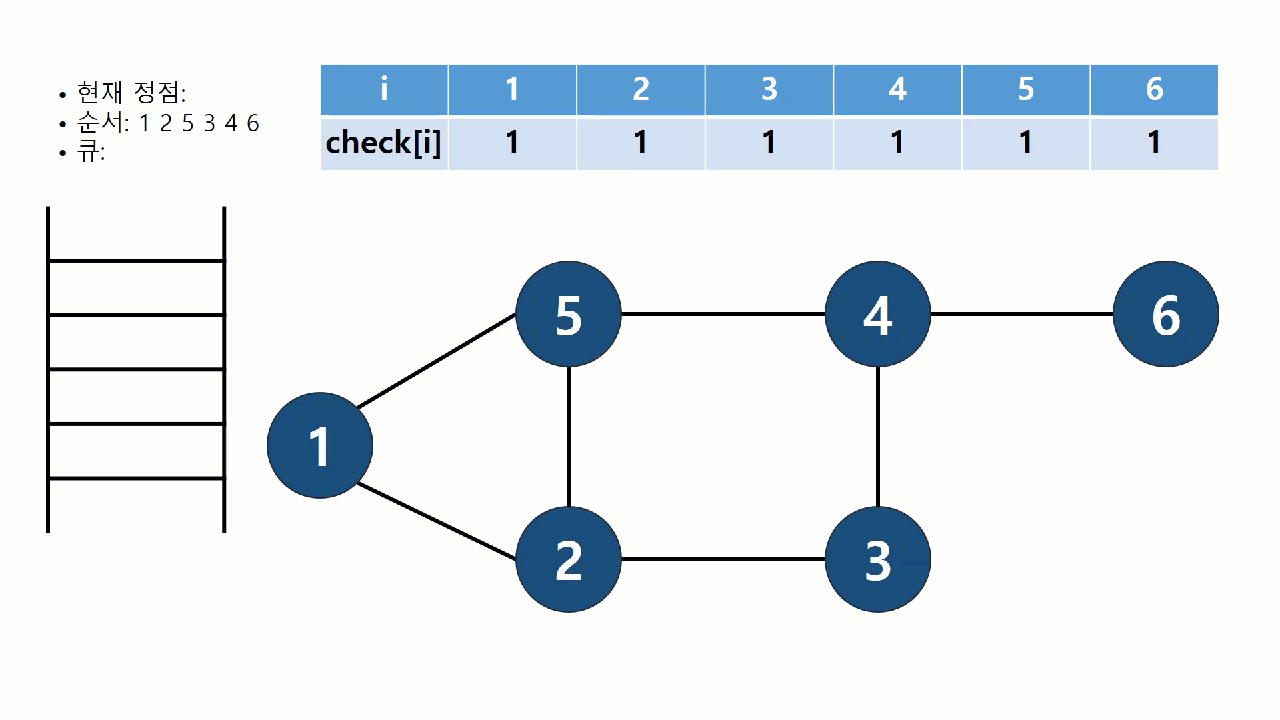
BFS 알고리즘

BFS란 너비 우선 탐색 알고리즘을 말한다.

https://velog.io/@polynomeer/%EA%B9%8A%EC%9D%B4-%EC%9A%B0%EC%84%A0-%ED%83%90%EC%83%89DFS

---

연결리스트로 BFS 구현하기

const graph = {
  A: ["B", "C"],
  B: ["A", "D"],
  C: ["A", "G", "H", "I"],
  D: ["B", "E", "F"],
  E: ["D"],
  F: ["D"],
  G: ["C"],
  H: ["C"],
  I: ["C", "J"],
  J: ["I"]
};

const BFS = (graph, startNode) => {
  const visited = []; // 탐색을 마친 노드들
  let needVisit = []; // 탐색해야할 노드들

  needVisit.push(startNode); // 노드 탐색 시작

  while (needVisit.length !== 0) { // 탐색해야할 노드가 남아있다면
    const node = needVisit.shift(); // queue이기 때문에 선입선출, shift()를 사용한다.
    if (!visited.includes(node)) { // 해당 노드가 탐색된 적 없다면
      visited.push(node); 
      needVisit = [...needVisit, ...graph[node]];
    }
  }
  return visited;
};

console.log(BFS(graph, "A"));
// ["A", "B", "C", "D", "G", "H", "I", "E", "F", "J"]

---

응용 문제 풀기! (2차원 배열로 BFS 구현하기)

📌 미로 탈출

N x M 크기의 직사각형 형태의 미로에 여러 마리의 괴물이 있어 이를 피해 탈출해야 한다. 현재 위치는 (1, 1)이고 미로의 출구는 (N,M)의 위치에 존재하며 한 번에 한 칸씩 이동할 수 있다. 괴물이 있는 부분은 0으로, 괴물이 없는 부분은 1로 표시되어 있다. 미로는 반드시 탈출할 수 있는 형태로 제시된다. 탈출하기 위해 움직여야 하는 최소 칸의 개수를 구하라. 칸을 셀 때는 시작 칸과 마지막 칸을 모두 포함해서 계산한다.

const direction = [[1, 0], [-1, 0], [0, 1], [0, -1]];

const bfs = (row, col, distance, queue, array) => {
  while (queue.length > 0) {
    const [curRow, curCol] = queue.shift();

    for (let [dx, dy] of direction) {
      const nextRow = dx + curRow;
      const nextCol = dy + curCol;

      if (
        0 <= nextRow &&
        nextRow < row &&
        nextCol >= 0 &&
        nextCol < col &&
        array[nextRow][nextCol] === 1 &&
        distance[nextRow][nextCol] === 0
      ) {
        distance[nextRow][nextCol] = distance[curRow][curCol] + 1;
        queue.push([nextRow, nextCol]);
      }
    }
  }
};

const solution = (row, col, arrayInput) => {
  const array = arrayInput.split('\n').map((value) =>
    value.split('').map(Number)
  );
  const distance = new Array(row).fill(0).map(() => new Array(col).fill(0));

  const queue = [];
  queue.push([0, 0]);
  distance[0][0] = 1;

  bfs(row, col, distance, queue, array);

  // 출구까지의 최소 칸 개수 반환
  return distance[row - 1][col - 1] ? distance[row - 1][col - 1] : -1;
};

const input = `101010
111111
000001
111111
111111`;

console.log(solution(5, 6, input));

---

DFS와 BFS 비교

소스 코드로 비교

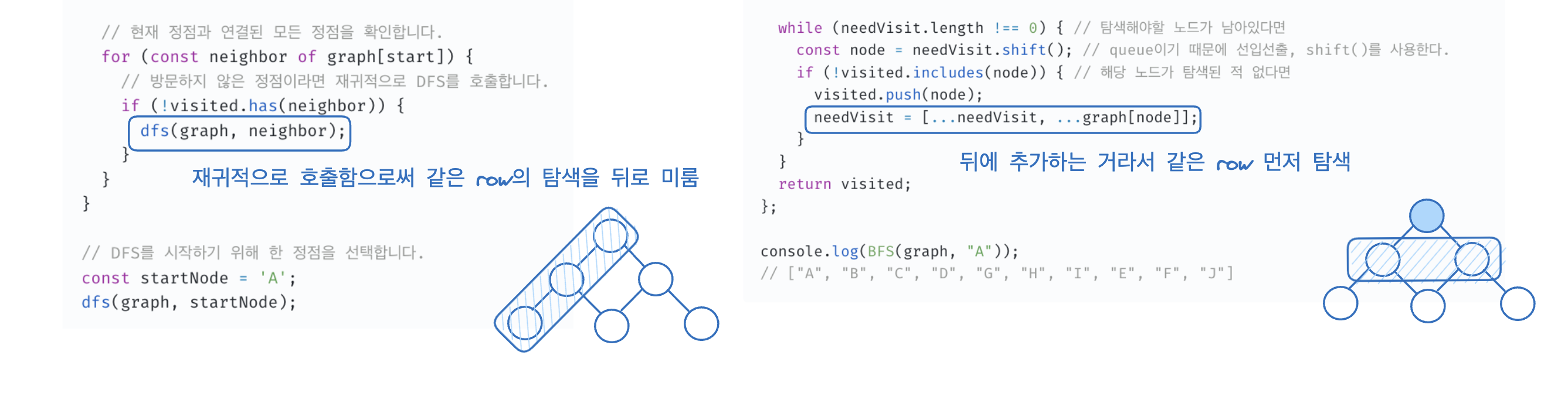
코드를 보면 DFS는 재귀적으로 호출되고, BFS는 큐에 다음 노드들을 넣습니다. 따라서 자신의 이웃 노드를 DFS는 뒤로 미루고, BFS는 바로 탐색합니다. 이렇게 탐색을 하게 되면 DFS는 깊이 우선으로 탐색하게 되고 BFS는 너비를 우선으로 탐색하게 되는것입니다!!

문제 유형

BFS는 최단 경로(시작과 끝이 정해진) 탐색에 유리하고, DFS는 모든 경로 탐색에 유리한 특성을 가지고 있는것 처럼 보입니다..!

• BFS : 최단거리, 최소 스탭(최소 동작), 동시 탐색(가능한 게임 상태 탐색), 이진탐색(중위 순회)
• DFS : 모든 그래프 순회, 백트래킹, 트리 높이 계산, 이진탐색(후위, 전위 순회)

간단한 예시로 이진탐색순회를 DFS는 전위, 후위 순회 / BFS로 중위 순회를 구현한 코드를 보여드리도록 하겠습니당!

// 이진 트리의 노드 클래스 정의
class Node {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

// DFS로 전위 순회 (Pre-order Traversal)
function preOrderDFS(node) {
  if (node === null) {
    return;
  }
  console.log(node.value); // 노드 처리
  preOrderDFS(node.left); // 왼쪽 서브트리 재귀 탐색
  preOrderDFS(node.right); // 오른쪽 서브트리 재귀 탐색
}

// DFS로 후위 순회 (Post-order Traversal)
function postOrderDFS(node) {
  if (node === null) {
    return;
  }
  postOrderDFS(node.left); // 왼쪽 서브트리 재귀 탐색
  postOrderDFS(node.right); // 오른쪽 서브트리 재귀 탐색
  console.log(node.value); // 노드 처리
}

// BFS로 중위 순회 (In-order Traversal)
function inOrderBFS(node) {
  if (node === null) {
    return;
  }

  const stack = [];
  let current = node;

  while (current || stack.length > 0) {
    while (current) {
      stack.push(current);
      current = current.left;
    }

    current = stack.pop();
    console.log(current.value); // 노드 처리
    current = current.right;
  }
}

// 예시 트리 생성
/*
         1
       /   \
      2     3
     / \   / \
    4   5 6   7
*/
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);

// 전위 순회 (DFS) 출력
console.log("Pre-order DFS:");
preOrderDFS(root);

// 후위 순회 (DFS) 출력
console.log("Post-order DFS:");
postOrderDFS(root);

// 중위 순회 (BFS) 출력
console.log("In-order BFS:");
inOrderBFS(root);

---

DFS, BFS

DFS가 아닌 BFS로 최단거리를 찾는 이유는?

DFS는 한 경로를 따라 가다가 다른 경로로 이동하기 때문에, 그래프의 깊숙한 부분을 탐색하는 데 유용하며, 순환을 감지하는 데도 사용될 수 있습니다. 하지만 최단 경로를 찾는 데는 적합하지 않습니다.

반면, BFS는 레벨 순서대로 탐색하기 때문에 최단 경로를 찾는 데 효과적입니다. 그래프에서 어떤 노드에서 다른 노드까지의 최단 경로를 찾아야 할 때 BFS를 사용하면, 그래프의 특성에 따라 최단 경로를 찾을 수 있습니다.

---