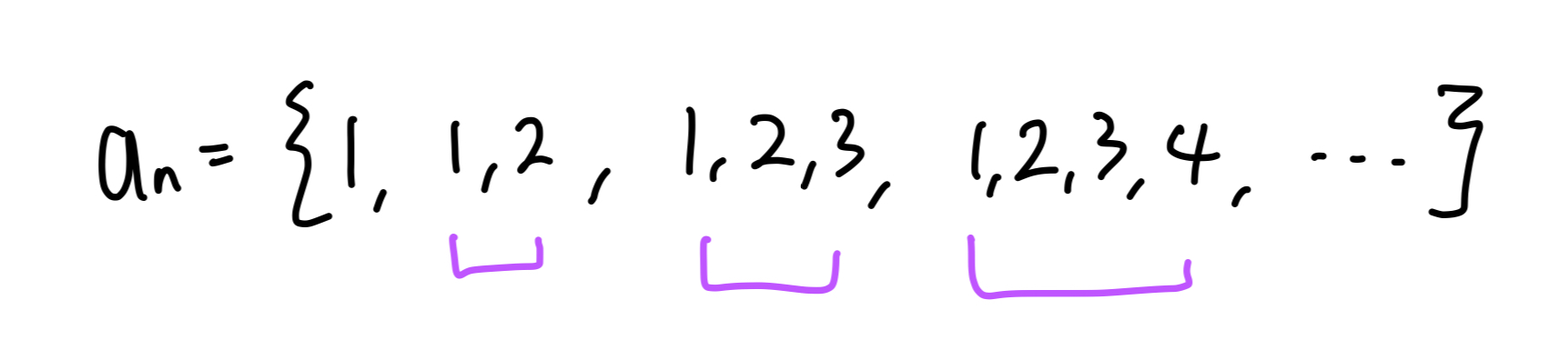[제로베이스] [기초 수학] 수열

1. 수열

수열
규칙성을 가지고 나열되어 있는 수들

---

2. 등차수열

등차수열
연속된 두 항의 차이가 일정한 수열
ex) A n = {2, 5, 8, 11, 14, ...}

• 공차
  연속된 두항의 차이 (등차수열에서 공차는 항상 일정하다)
• 일반항
  등차수열의 초항을 A 1, 연속된 두항의 차이를 공차 즉 d 라고 둔다면 n번째 항(A n)은
  A n = A 1 + (n-1) d
• 등차중항
  연속된 세 항에서 가운데 항
  2 A n = A n-1 + A n+1
• 등차수열의 합
  A 1 + ... + A n = S n 으로 두면
  S n = n(A 1 + A n) / 2
  S n = n(2 A 1 + (n-1) d) / 2
  두 개의 공식으로 표현이 가능하다.

---

다음 수열을 보고 n번째 항의 값을 출력하는 프로그램을 만들어보자.
A n = {2, 5, 8, 11, 14, ...}

a1 = int(input('a1 입력: '))
d = int(input('공차 입력: '))
n = int(input('n 입력: '))

for i in range(1,n+1):
    print(f'{i}번째 항의 값: {a1 + (i-1)*d}')

print(f'{n}번째 항의 값: {a1+(n-1)*d}')

a1 입력: 2
공차 입력: 3
n 입력: 7
1번째 항의 값: 2
2번째 항의 값: 5
3번째 항의 값: 8
4번째 항의 값: 11
5번째 항의 값: 14
6번째 항의 값: 17
7번째 항의 값: 20
7번째 항의 값: 20

---

다음 수열을 보고 n번째 항까지의 합을 출력하는 프로그램을 만들어보자.
A n = {5, 9, 13, 17, 21, ...}

a1 = int(input('a1 입력: '))
d = int(input('공차 입력: '))
n = int(input('n 입력: '))
Sn = a1
print(f'1번째 항까지의 합: {Sn}')

for i in range(2,n+1):
    an = a1 + (i-1)*d
    Sn += an
    print(f'{i}번째 항까지의 합: {Sn}')
    
print(f'{n}번째 항까지의 값: {Sn}')

a1 입력: 5
공차 입력: 4
n 입력: 7
1번째 항까지의 합: 5
2번째 항까지의 합: 14
3번째 항까지의 합: 27
4번째 항까지의 합: 44
5번째 항까지의 합: 65
6번째 항까지의 합: 90
7번째 항까지의 합: 119
7번째 항까지의 값: 119

---

3. 등비수열

등차수열
연속된 두 항의 비가 일정한 수열
ex) A n = {1, 3, 9, 27, 81, ...}

• 공비
  연속된 두항의 비 (등비수열에서 공비는 항상 일정하다)
• 일반항
  등차수열의 초항을 A 1, 연속된 두항의 차이를 공비 즉 r 라고 둔다면 n번째 항(A n)은
  A n = A 1 * r^(n-1)
• 등비중항
  연속된 세 항에서 가운데 항
  (A n)^2 = A n-1 * A n+1
• 등비수열의 합
  A 1 + ... + A n = S n 으로 두면
  S n = A 1*(1- (r^n)) / (1-r)

---

다음 수열을 보고 n번째 항의 값을 출력하는 프로그램을 만들어보자.
A n = {2, 4, 8, 16, 32, ...}

a1 = int(input('a1 입력: '))
r = int(input('공비 입력: '))
n = int(input('n 입력: '))

for i in range(1,n+1):
    print(f'{i}번째 항의 값: {a1 * (r**(i-1))}')

print(f'{n}번째 항의 값: {a1 * (r**(n-1))}')

a1 입력: 2
공비 입력: 2
n 입력: 7
1번째 항의 값: 2
2번째 항의 값: 4
3번째 항의 값: 8
4번째 항의 값: 16
5번째 항의 값: 32
6번째 항의 값: 64
7번째 항의 값: 128
7번째 항의 값: 128

---

다음 수열을 보고 n번째 항까지의 합을 출력하는 프로그램을 만들어보자.
A n = {5, 15, 45, 135, 405, ...}

a1 = int(input('a1 입력: '))
r = int(input('공비 입력: '))
n = int(input('n 입력: '))

Sn = a1
print(f'1번째 항까지의 합: {Sn}')

for i in range(2, n + 1):
    an = a1 * (r ** (i - 1))
    Sn += an
    print(f'{i}번째 항까지의 합: {Sn}')

print(f'{n}번째 항까지의 값: {Sn}')

a1 입력: 5
공비 입력: 3
n 입력: 7
1번째 항까지의 합: 5
2번째 항까지의 합: 20
3번째 항까지의 합: 65
4번째 항까지의 합: 200
5번째 항까지의 합: 605
6번째 항까지의 합: 1820
7번째 항까지의 합: 5465
7번째 항까지의 값: 5465

---

4. 시그마(Σ)

Σ란 수열의 합을 나타내는 기호이다.

---

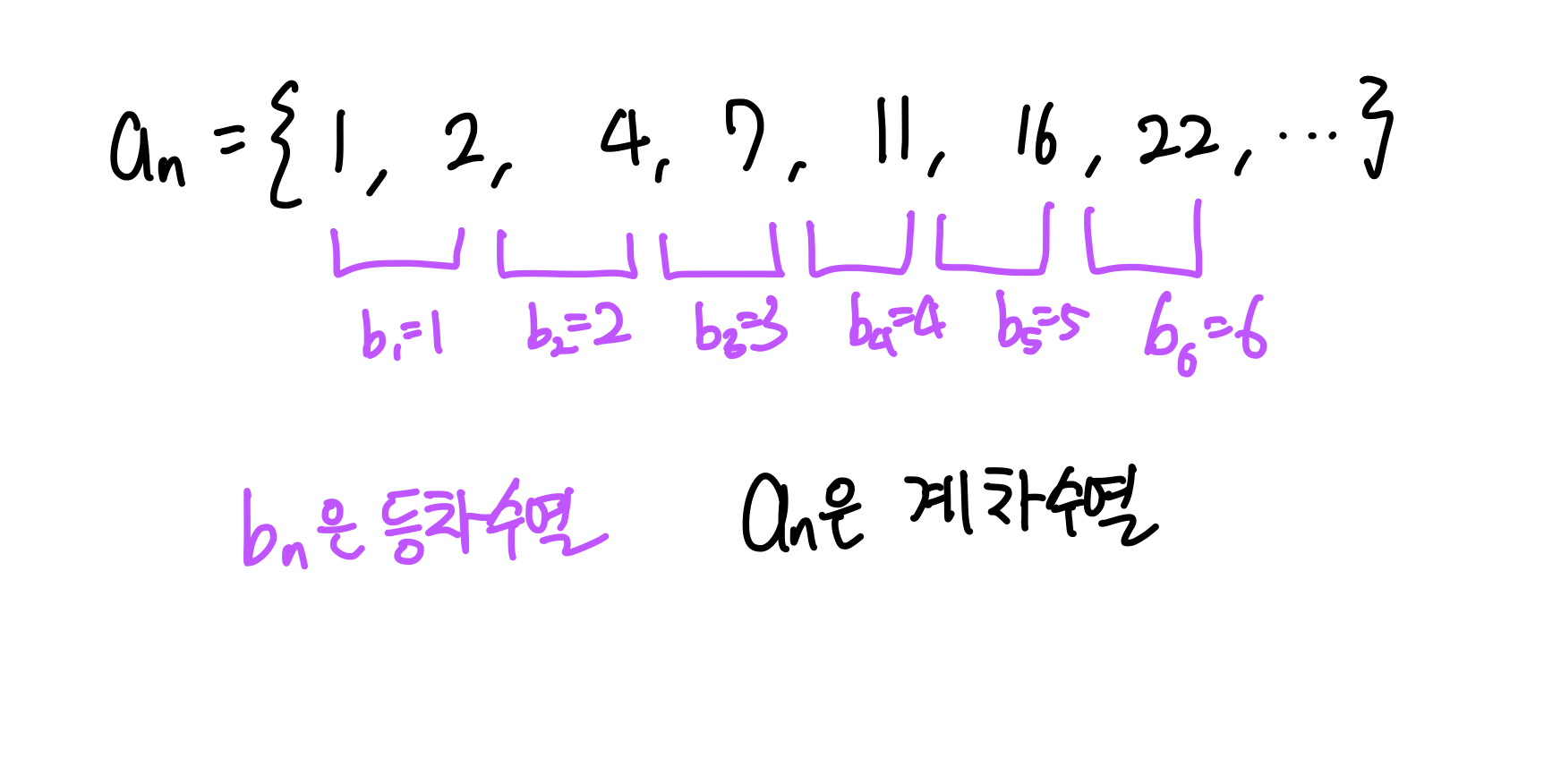
5. 계차수열

계차수열
어떤 수열의 인접하는 두 항의 차로 이루어진 또 다른 수열

---

다음 수열을 보고 n번째 항의 값을 출력하는 프로그램을 만들어보자.
An = {3, 7, 13, 21, 31, 43, 57}

a1 = int(input('a1 입력: '))
n = int(input('n 입력: '))

b1 = int(input('b1 입력: '))
d = int(input('d 입력: '))

an = a1
bn = b1

for i in range(1,n):
    an += bn
    bn += d

print(f'{n}번째 항은 {an}')

a1 입력: 3
n 입력: 7
b1 입력: 4
d 입력: 2
7번째 항은 57

---

6. 피보나치 수열

피보나치 수열
A n = A n-2 + A n-1

---

7. 군수열

군수열
여러 개의 항을 묶었을 때 규칙성을 가지는 수열

---

다음 수열을 보고 n번째 항의 값을 출력하는 프로그램을 만들어보자.

1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1, 2, 3, 4, 5, ...

group = 0
total = 0

n = int(input('n항 입력: '))

while total < n:
    group += 1 # 최종 group값이 군
    total += group

an = n - total + group

print(f'{n}항: {an}')

n항 입력: 10
10항: 4