[PS]11266

문제 이해

11266번: 단절점 이번 문제는 그래프 관련 문제와 익숙해지고 싶어서 골라본 문제이다. 문제 이름부터가 굉장히 심플한 알고리즘을 사용할 것 같았다.

문제는 이렇다.

그래프 $G$가 있을 때 , 각각의 정점을 $v_1,v_2,v_3,...,v_n$이라고 하자. 이 때 $G$에서 $v_i$와 그와 연결된 간선을 제거한 이후의 connected component의 개수가 이전과 달라지면 그 점을 단절점이라고 부른다. 그래프 $G$의 단절점의 개수와 그 index를 모두 구하시오.

문제 풀이

시간 제한은 1초, $v$는 최대 $10^4$개, $e$는 최대 $10^5$개였다. connected component를 계산하는 알고리즘은 DFS와 동일하게 $O(V+E)$로 볼 수 있었기 때문에 각각의 정점을 제거한 이후 연결요소를 계산하면 시간초과가 날 것이 분명했다.

그 말인즉슨 DFS를 한 번 도는 동안 각각의 정점이 단절점인지 아닌지 판별해야 한다는 뜻이다.

문제를 풀려고 여러 방식을 시도하다보면, 정확히 어떤 연관성이 있는지는 모르더라도 그래프 내의 사이클(Cycle)이 중요한 고려 대상이라는 사실을 알 수 있다. 그렇다면 이렇게 한 번 생각해보자. DFS로 정점을 하나하나 탐색해나가다 보면 Spanning Tree가 만들어지는데, 이 트리에 속하지 못한 간선들은 자동으로 cycle을 만들게 된다고 볼 수 있지 않을까?

Spanning Tree에 속하지 못한 간선은 그래프의 cycle을 만든다.

다음과 같은 Tree를 생각해보자.

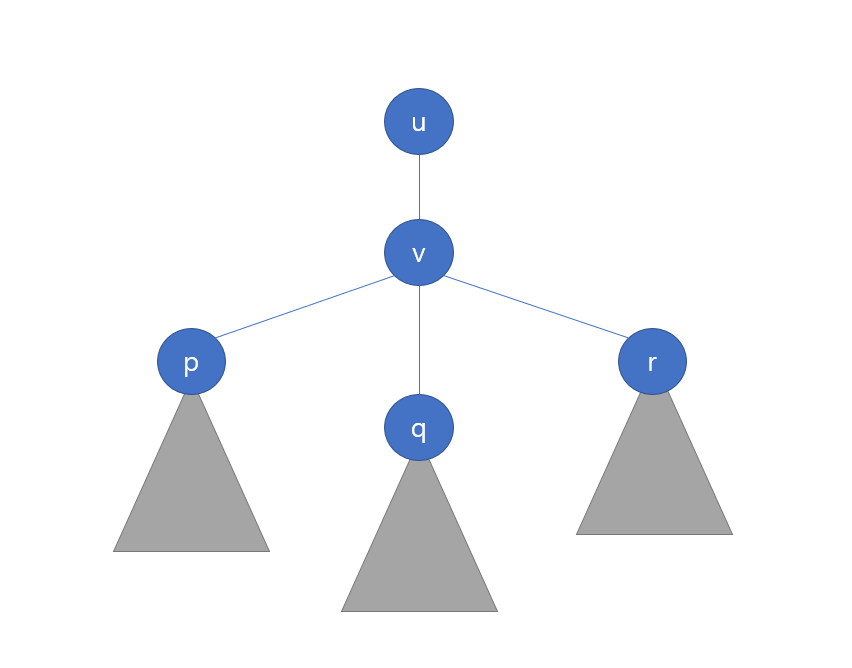
정점 $v$는 $p,q,r$이라는 자식 노드가 있고 각각은 subtree를 가지고 있는 상황이다.
이 때, 이 트리가 어떤 그래프의 Spanning Tree이며 지금 $v$의 단절점 여부를 확인해야 한다고 가정해볼 수 있다. $v$가 없어지더라도 $u$와 $p,q,r$이 연결되기 위해서는

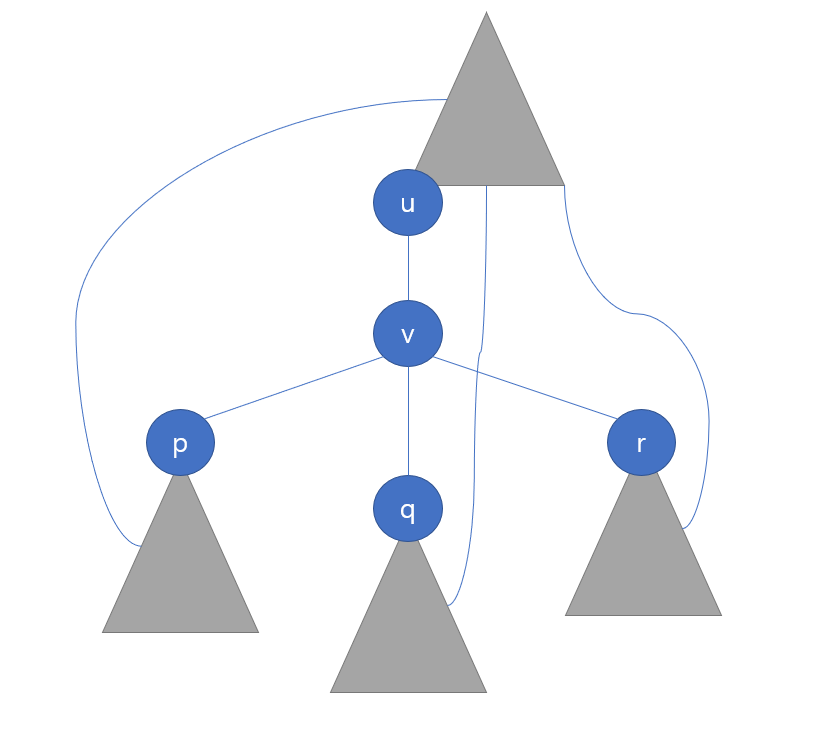
위와 같이 $p,q,r$의 subtree에서 나오는 Spanning Tree에 속하지 못한 간선들이 정점 $v$보다 부모인 노드와 연결되어 있어야만 한다. 바로 이 점을 이용하면 단절점 문제를 해결할 수 있다.

우선 discover[i] 배열에는 dfs로 그래프의 각 노드를 탐색하면서 i번째 노드가 몇 번째로 탐색되었는지를 저장한다. 그리고, dfs(v) 함수는 정점 $v$와 연결된 노드 중 아직 탐색되지 않은 노드들(위 그림에서는 $p,q,r$)에 대해서는 그 subtree에서 뻗어나가는 간선이 가리키는 노드의 discover[]중 가장 작은 값을, 한 번 탐색된 노드에 대해서는 그 노드의 discover[]를 가지고 와서 그 중 가장 작은 값을 반환한다. 그리고 이 과정에서 하나의 자식 노드에서라도 dfs()의 값이 discover[v]라면, $v$는 절단점이 되는 것이다.

이렇게 dfs(v) 함수를 구성하면, 함수 이름처럼 dfs함수를 재귀적으로 사용해 모든 정점의 단절점 여부를 확인할 수 있게 된다. 다만 여기서 주의할 점은 Spanning Tree의 루트 노드의 경우 이 정점이 단절점이든 아니든 상관없이 단절점으로 분류된다는 것이다. 이 경우 루트 노드와 연결된 간선이 2개 이상이면 단절점으로, 2개 미만이면 단절점이 아닌 것으로 분류하는 코드를 추가해주어야 한다.

여기서 "$p$랑 $q$가 연결되어 있으면 어떡하나요?"와 같은 질문이 나올 수도 있다. 하지만 DFS 방식으로 Spanning Tree를 그리기 때문에 애초에 두 정점의 subtree가 연결되어 있었다면 하나의 subtree처럼 그려지지 위 그림처럼 그려질 일은 없다.

코드

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

int v, e;
vector<int> vc[10001];
int discover[10001];
bool cutpoint[10001];
int cnt = 0;

int dfs(int node, bool isRoot)
{
    discover[node] = cnt++;
    int ret = discover[node];
    int children = 0;
    for(auto next : vc[node])
    {
        if(discover[next]==-1)
        {
            children++;
            int subtree = dfs(next, false);
            if(!isRoot && subtree>=discover[node]) cutpoint[node] = true;
            ret = min(ret, subtree);
        }
        else ret = min(ret, discover[next]);
    }
    if(isRoot) cutpoint[node] = (children>=2);
    return ret;
}

int main()
{
    cin.sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> v >> e;
    for(int i=0; i<e; i++)
    {
        int a, b;
        cin >> a >> b;
        vc[a-1].push_back(b-1);
        vc[b-1].push_back(a-1);
    }
    for(int i=0; i<v; i++)
    {
        discover[i] = -1;
        cutpoint[i] = false;
    }
    for(int i=0; i<v; i++)
        if(discover[i]==-1) dfs(i, true);
    queue<int> q;
    for(int i=0; i<v; i++)
        if(cutpoint[i]) q.push(i+1);
    cout << q.size() << '\n';
    while(!q.empty())
    {
        cout << q.front() << ' ';
        q.pop();
    }
    cout << '\n';
    return 0;
}

정리

이틀동안 이 문제 때문에 고민했지만 결국 풀 수 없었다. 마지막 지푸라기 잡는 심정으로 종만북의 그래프 부분을 정독하려고 하다가 절단점 문제의 풀이가 발견해 참지 못하고 답을 읽어버렸다. 코드까지 읽고 보니 내 방식대로 다시 코드를 짜려고 해도 답 코드가 계속 머리에서 맴돌아 알고리즘을 적용한 나만의 코드를 적을 수 없었다. 그래서 알고리즘만 velog에 정리해놓고 나중에 다시 한 번 풀어봐야 할 것 같다.

문제를 푸는 데에 있어서 생소하거나 처음듣는 개념이 없었다. 그런데도 답을 떠올리지 못했다는 것은 아직 경험이 부족하다는 뜻일 것이다. 이렇게 된거 종만북 그래프 부분을 제대로 읽고, 연습문제를 많이 풀어봐야겠다.