문제 풀러가기

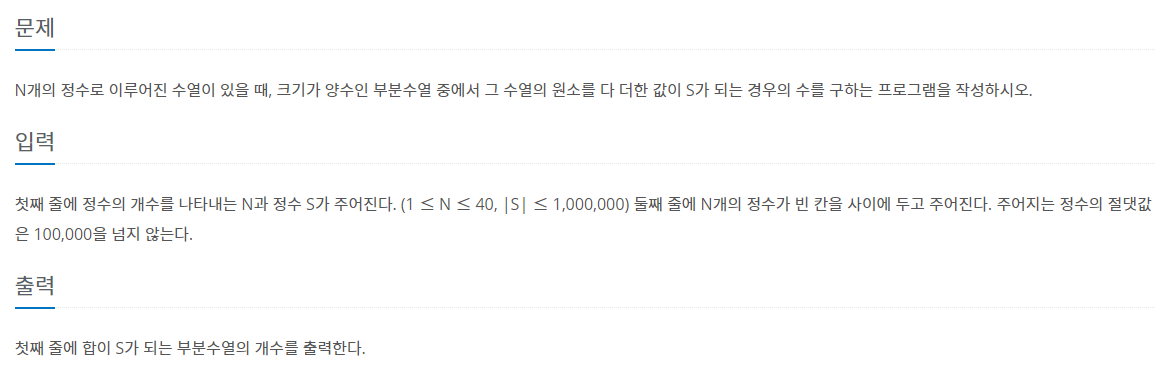
Problem

Solution

• 부분수열의 합을 구하는 모든 경우의 수를 고려해야 한다. → Backtracking
• 하지만 1<=N<=40 이므로 아무런 조건의 변형없이 모든 경우의 수를 구할 경우
  O(2^40) > 1초로 time limit 발생
• 따라서 N개의 정수로 이루어진 수열을 N/2개의 정수로 이루어진 배열(arr1),
  N-(N/2)개의 정수로 이루어진 배열(arr2)로 나누어 경우의 수를 구함
• 모든 경우의 수의 부분수열 합 배열을 arr1과 arr2에서 각각 생성 → (sarr1, sarr2)
• sarr1의 element의 값이 X라고 할 때, sarr2의 element 중 S-X가 존재하는지
  Binary Search를 통해 확인

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <cmath>
#include <queue>
#include <map>

using namespace std;

int N, S;
vector<int> arr[2]; // N/2, N - N/2 배열
vector<int> sarr[2]; // sum 배열
/* 모든 합 경우의 수를 구해주는 함수 */
void solve(int sum, int start, int n){
	int last;
	if(n == 0) last = N/2;
	else last = N - N/2;
	for(int i=start+1; i<last; i++){
		sarr[n].push_back(sum + arr[n][i]);
		solve(sum + arr[n][i], i, n);
	}
}
/* 이분탐색 함수 */
bool binarySearch(int low, int high, int x){
	if(low > high)
		return false;
	int mid = (low + high) / 2;
	int mid_value = sarr[1][mid];
	if(mid_value == x) 	return true;
	else if(mid_value > x)	return binarySearch(low, mid - 1, x);
	else	return binarySearch(mid + 1, high, x);
	
}

int main(){
	scanf("%d %d", &N, &S);
	
	arr[0] = vector<int>(N/2);
	arr[1] = vector<int>(N-N/2);
	
	for(int i=0; i<N/2; i++)
		scanf("%d", &arr[0][i]);
	for(int i=0; i<N-N/2; i++){
		scanf("%d", &arr[1][i]);
	}
	
	/* sarr[0] 생성 */
	int n = 0;
	solve(0, -1, n);
	sort(sarr[n].begin(), sarr[n].end()); // sarr 오름차순 정렬
	
	/* sarr[1] 생성 */
	n = 1;
	solve(0, -1, n);
	sort(sarr[n].begin(), sarr[n].end()); // sarr 오름차순 정렬
	
	int sarr0_len = sarr[0].size();
	int sarr1_len = sarr[1].size();
	
	long long num = 0;
	/* sarr0 */
	for(int i=0; i<sarr0_len; i++){
		if(sarr[0][i] == S)
			num++;
	}
	/* sarr1 */
	for(int i=0; i<sarr1_len; i++){
		if(sarr[1][i] == S)
			num++;
	}
	
	map<int, int> m;
	/* key : 부분수열의 합
    	   value: 해당 부분수열 합의 개수 
    	   map 초기화 */
	for(int i=0; i<sarr1_len; i++){
		int key = sarr[1][i];
		if(m[key] == 0) m[key] = 1;
		else m[key] += 1;
	}
		
	/* sarr0 + sarr1 */
	for(int i=0; i<sarr0_len; i++){
		int x = sarr[0][i];
		int y = S - x;
		if(binarySearch(0, sarr1_len - 1, y))
			num += m[y];
	}
	
	printf("%lld \n", num);
}

Result

• 같은 부분수열의 합이 발생하는 경우를 생각하지 않았다.
• vector의 크기를 작게 할당하여 InvalidNextSize Runtime Error 발생
• sarr1 혹은 sarr2 배열의 원소 중에 S가 존재하는 경우를 생각하지 않았다.
• 모든 경우의 수를 int형 정수로 표현할 수 있을 것으로 생각
  int형 정수의 범위 : [-2^31 ~ 2^31 - 1]