2개 이하로 다른 비트

문제 안내

문제 설명

• 양의 정수 x에 대한 함수 f(x)를 다음과 같이 정의합니다.

  x보다 크고 x와 비트가 1~2개 다른 수들 중에서 제일 작은 수

• 예를 들어,

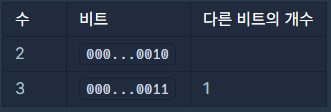
  • f(2) = 3 입니다.
  • 다음 표와 같이 2보다 큰 수들 중에서 비트가 다른 지점이 2개 이하이면서 제일 작은 수가 3이기 때문입니다.
    

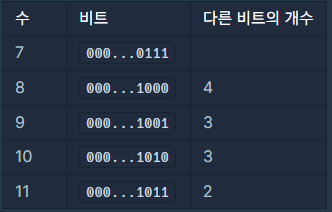
  • f(7) = 11 입니다.
  • 다음 표와 같이 7보다 큰 수들 중에서 비트가 다른 지점이 2개 이하이면서 제일 작은 수가 11이기 때문입니다.
    

• 정수들이 담긴 배열 numbers가 매개변수로 주어집니다.

• numbers의 모든 수들에 대하여 각 수의 f 값을 배열에 차례대로 담아 return 하도록 solution 함수를 완성해주세요.

제한사항

  - 1 ≤ numbers의 길이 ≤ 100,000
    0 ≤ numbers의 모든 수 ≤ 10의 15제곱

입출력 예

	numbers = [2, 7]   →   result = [3, 11]

풀이

Logic 설명 (Code 1 관련)

• Code 2를 개선
  • if문을 2번 사용하여 총 3개의 경우를 고려해야 했던 부분을 개선
    → if 문을 1번만 사용
  • 중요한 것은, 가장 낮은자리에서부터 0을 찾아가서 해당 위치에서 01을 10으로 변경하기만 하면 된다는 것!

    1) 맨 첫 번째 자리가 0인 경우를 고려하여 맨 뒤에 1을 추가
    2) 모든 자리의 수가 1인 경우를 고려하여 맨 앞에 0을 추가

Code 1

# 비트가 2다른 지점이 2개 이하이면서 가장 작은 수를 계산하는 함수
def cal(n):
    # 주어진 수를 2진수로 변환
    # 변환 후, 맨 앞에 0을, 맨 뒤에는 1을 삽입
    bin_n = list("0"+bin(n)[2:]+"1")
    # 기존의 2진법 수들 중 첫 번째 자리(가장 낮은 자리)의 수부터 반복
    for i in reversed(range(len(bin_n)-1)):
    	# 만약, 해당 자리의 수가 0이라면
        if bin_n[i] == '0':
        	# 그 자리의 수(0)와 그보다 하나 낮은 자리의 수(1)를 변경함
            bin_n[i], bin_n[i+1] = "1","0"
            # 다했으면 for문 종료
            break
    # 변경한 수의 가장 낮은 자리 수를 제외하고 10진법의 수로 바꿔서 반환
    return int("".join(bin_n[:-1]),2)

# numbers 내의 각 값에 대한 결과를 리스트로 반환하는 함수
def solution(numbers):
    return [cal(n) for n in numbers]

Logic 설명 (Code 2 관련)

• 2진수로 변경하였을 때 0이 있는지를 확인해야 하며, 0이 있다면 어느 위치에 있는지를 보고 경우를 나눠 코드를 작성해야 함.

  1. 변경한 2진수에서 0이 맨 첫번째 자리(2의 0제곱 자리수)에 있는 경우
     • 원래 주어진 수가 짝수임을 의미.
     • 원래 수에 1을 더하면 2진수에서 맨 첫번째 자리만 달라지므로, 비트가 1개 달라짐. → 문제 조건을 충족
  2. 변경한 2진수에서 0이 없는 경우
     • 원래 주어진 수가 2의 거듭제곱보다 1이 작은 수임을 의미 (이거 신경 안써도 됨)
     • 변경한 2진수 앞에 0이 있는 것으로 간주하고, 맨 앞 두자리에 있는 0과 1의 자리를 바꾸면 됨.
     • 변경한 수는 원래 수와 비트가 2개 달라짐. → 문제 조건을 충족
  3. 변경한 2진수에서 0이 중간에 껴있는 경우
     • 해당 0의 위치를 찾아서, 그 자리수의 0과 그 자리수보다 하나 작은 큰 자리수에 있는 1의 위치를 바꾸면 됨. → '01'을 '10'으로 바꿔준다는 뜻임
     • 변경한 수는 원래 수와 비트가 2개 달라짐. → 문제 조건을 충족

Code 2

# 비트가 2다른 지점이 2개 이하이면서 가장 작은 수를 계산하는 함수
def cal(n):
	#결과값을 받을 변수를 result로 할당
    result = 0
    # 주어진 수를 2진수(str)로 변환
    n_bin = bin(n)[2:]
    
	# 변경한 2진수에서 0이 맨 첫번째 자리(2의 0제곱 자리수)에 있는 경우
    # 그 말인즉, 원래 수가 짝수임을 의미
    if n% 2 == 0:
        # 원래 수에 1을 더하면 2진수에서 맨 첫번째 자리만 달라지므로, 비트가 1개 달라짐. 
        # 문제 조건을 충족하게 되어 (n+1)이 결과값이 됨.
        result = n+1
        
    # 그렇지 않은 경우에 대해 생각
    else:
    	# 변경한 2진수에 0이 아예 없는 경우 → 전부 1만 있는 경우
        # 비트가 2개 달라져야 나보다 큰 최소의 수를 찾을수가 있고, 맨 앞에서 바꿔줘야 함
        # 맨 앞자리 수의 '1'을 '10'으로 바꿔주면 됨.
        if '0' not in n_bin:
        	# 변경한 2진수에서 맨 앞의 수를 '10'으로 대체
            result = int('10'+n_bin[1:],2)
        # 변경한 2진수에서 중간 어딘가에 0이 있는 경우
        # 비트가 2개 달라져야 나보다 큰 최소의 수를 찾을 수 있음.
        # 그 자리의 0과 그 보다 하나 더 작은 자리에 있는 1의 값을 변경해주면 됨
        else:
        	# 0의 위치를 제일 낮은자리부터 찾아야 하므로 rfind 함수를 사용
            idx_zero = n_bin.rfind('0')
            # 0의 자리수보다 큰 자리수는 그대로 사용하고, 
            # 0과 그 보다 한 자리 작은 자리에 있는 수는 위치를 바꾸어 '10'으로 사용하고,
            # 나머지 자리수는 그대로 사용
            # 합친 2진수(str)을 10진수로 변경
            result = int(n_bin[:idx_zero]+'10'+n_bin[idx_zero+2:],2)
    return result

def solution(numbers):
    return [cal(n) for n in numbers]

Logic 설명 (Code 3 관련)

• 아주 처음에 짜서 제출했던 코드
• 발생 가능한 경우를 고려하여 숫자들을 한 20개 정도 예시들면서 규칙을 찾아봤었음.

Code 3

# 2진수로 변환
def trans(n):
    # n을 2진수 문자열로 변환 시 사용할 변수를 지정
    num = ""
    # n이 0보다 크다면 반복 시행
    while n:
        # 2로 나누면서 몫과 나머지를 계속 갱신
        n, mod = divmod(n, 2)
        # 나머지를 num에 추가함
        # ※ 주의!! : 낮은 자리의 수가 num에서 앞에 위치함
        num += str(mod)
    return num

# 문자열 중간에 0이 껴있을 때, 비트가 다른 지점이 2개면서 제일 작은 수로 변환
def trans2(n: str):
    # 입력받은 문자열을 하나씩의 요소로 분리한 리스트로 변환 후 각 요소를 숫자로 변환 
    n = list(map(int,list(n)))
    # 주어진 수를 10진법의 수로 변경할 때 사용할 변수 지정
    answer = 0
    # 반복문 시행
    for i in range(len(n)):
        # 만약, 해당 자리의 수가 0이라면
        if n[i] == 0 :
            # 현재 자리보다 하나 낮은 자리의 수와 0과 1을 서로 바꿔줌
            # 이렇게 하면, 원래 값보다 더 큰 최소의 2진수로 변경됨
            n[i-1], n[i] = 0, 1
            break
    # 주어진 2진수를 10진수로 변경하기
    for i in range(len(n)):
        answer += n[i] * 2**(i)
    return answer

# 나보다 큰 수들 중에서 비트가 다른 지점이 2개 이하이면서 제일 작은 수를 찾기
def solution(numbers):
    #결과를 담을 빈 리스트 생성
    result = []
    for i in numbers:
        # i의 2진수의 길이를 leng이라는 변수에 할당
        leng = len(trans(i))
        # 만약 i가 2의 배수이거나 4로 나눈 나머지가 1인 경우
        if i %2 == 0 or i % 4 == 1 :
            result.append(i+1)
        # 만약 i가 8로 나눈 나머지가 3인 경우
        elif i % 8 == 3 :
            result.append(i+2)
        # 만약 (i+1)이 2의 거듭제곱인 경우
        elif (i+1) % (2**leng) == 0:
            result.append(i+2**(leng-1))
        # 그 외 모든 경우
        else:
            result.append(trans2(trans(i)))
    return result