Programmers - k진수에서 소수 개수 구하기 [Python3]

📕 문제 설명

양의 정수 n이 주어집니다. 이 숫자를 k진수로 바꿨을 때, 변환된 수 안에 아래 조건에 맞는 소수(Prime number)가 몇 개인지 알아보려 합니다.

• 0P0처럼 소수 양쪽에 0이 있는 경우
• P0처럼 소수 오른쪽에만 0이 있고 왼쪽에는 아무것도 없는 경우
• 0P처럼 소수 왼쪽에만 0이 있고 오른쪽에는 아무것도 없는 경우
• P처럼 소수 양쪽에 아무것도 없는 경우
• 단, P는 각 자릿수에 0을 포함하지 않는 소수입니다.
  - 예를 들어, 101은 P가 될 수 없습니다.

예를 들어, 437674을 3진수로 바꾸면 211020101011입니다. 여기서 찾을 수 있는 조건에 맞는 소수는 왼쪽부터 순서대로 211, 2, 11이 있으며, 총 3개입니다. (211, 2, 11을 k진법으로 보았을 때가 아닌, 10진법으로 보았을 때 소수여야 한다는 점에 주의합니다.) 211은 P0 형태에서 찾을 수 있으며, 2는 0P0에서, 11은 0P에서 찾을 수 있습니다.

정수 n과 k가 매개변수로 주어집니다. n을 k진수로 바꿨을 때, 변환된 수 안에서 찾을 수 있는 위 조건에 맞는 소수의 개수를 return 하도록 solution 함수를 완성해 주세요.

📌 제한사항

• 1 ≤ n ≤ 1,000,000
• 3 ≤ k ≤ 10

📌 입출력 예

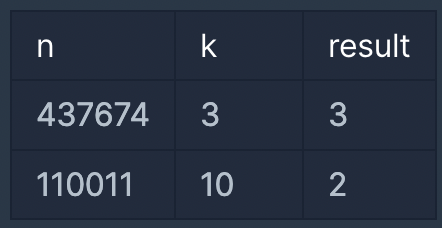
입출력 예 #2
110011을 10진수로 바꾸면 110011입니다. 여기서 찾을 수 있는 조건에 맞는 소수는 11, 11 2개입니다. 이와 같이, 중복되는 소수를 발견하더라도 모두 따로 세어야 합니다.

💡 문제 풀이

1. n을 k진법으로 나타낸다.
2. k진법을 나타낸 수 m을 0 앞뒤로 잘라서 소수인지 판단한다.

이 순서대로 코드를 작성할 때 핵심적으로 사용되는 알고리즘 두가지가 있다.

1️⃣ n을 k진법으로 나타내는 방법

def jinsoo(n, k):
    x = ''

    while n > 0:
        n, mod = divmod(n, k)
        x += str(mod)

    return x[::-1]

• 파이썬이 제공하는 divmod(n,k) 함수는 n을 k로 나누었을 때, 몫과 나머지를 한번에 구하는 함수이다.

2️⃣ 소수 판별

def isPrime(n):
    if n < 2:
        return False
    for i in range(2, int(math.sqrt(n))+1):
        if n % i == 0:
            return False
    return True

처음에는 for 문의 range를 2부터 n까지 하였는데,
1번 테스트 케이스에서 시간 초과가 발생했다.
n 대신 n의 제곱근까지만 for 문을 실행시키니 모든 테케를 통과하였다..! 👍🏻

👩🏻‍💻 전체 코드

import math

def solution(n, k):
    answer = 0

    if k == 10:
        m = str(n)
    else: 
        # n을 k진법으로 나타내기 -> m
        x = jinsoo(n, k)
        m = str(x)

    # m을 0 앞뒤로 잘라서 소수인지 판단
    i = 0
    while i < len(m):
        # print('i = ', i)
        if m[i] != 0:
            temp = ''
            while i < len(m) and m[i] != '0':
                temp += m[i]
                i += 1

            if temp != '' and isPrime(int(temp)):
                answer += 1
            i += 1
        else:
            i += 1

    return answer

def jinsoo(n, k):
    x = ''

    while n > 0:
        n, mod = divmod(n, k)
        x += str(mod)

    return x[::-1] 

def isPrime(n):
    if n < 2:
        return False
    for i in range(2, int(math.sqrt(n))+1):
        if n % i == 0:
            return False
    return True