DFS/BFS
DFS와 BFS는 대표적인 그래프 탐색 알고리즘
탐색
- 탐색이란 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정을 의미
- 일반적으로 그래프, 트리 등의 자료구조 안에서 탐색을 하는 문제를 자주 다룬다.
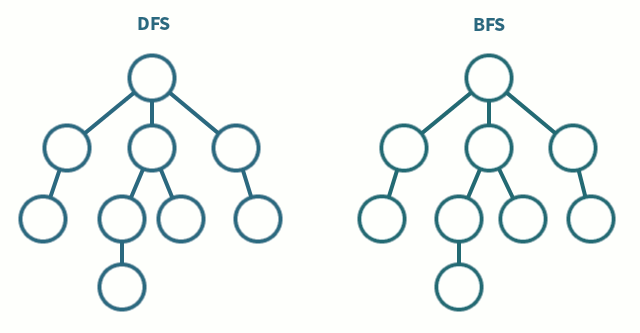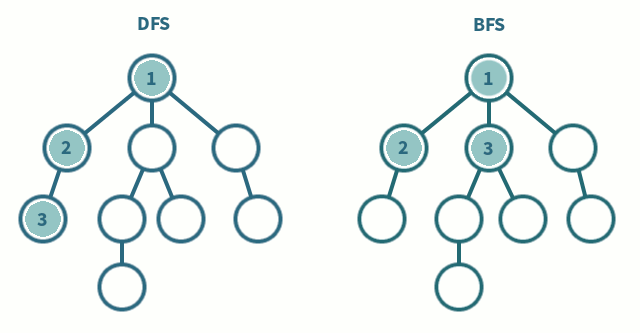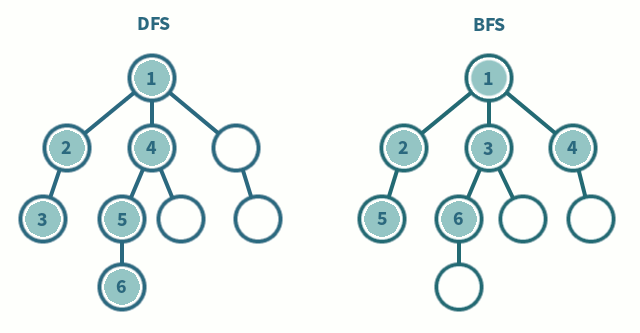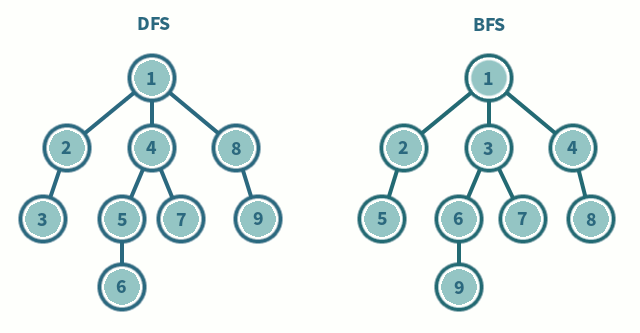
DFS (Depth-First Search)
그래프와 트리의 깊은 부분을 우선적으로 탐색하는 알고리즘
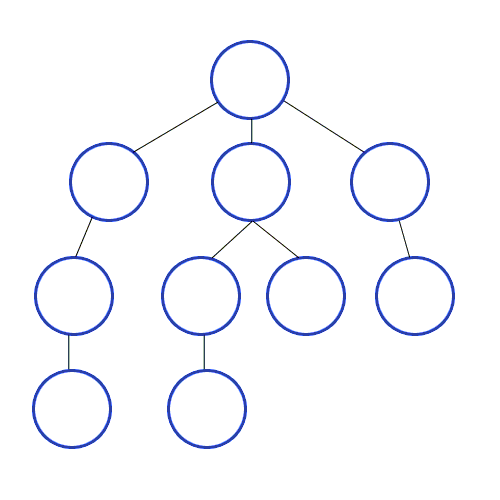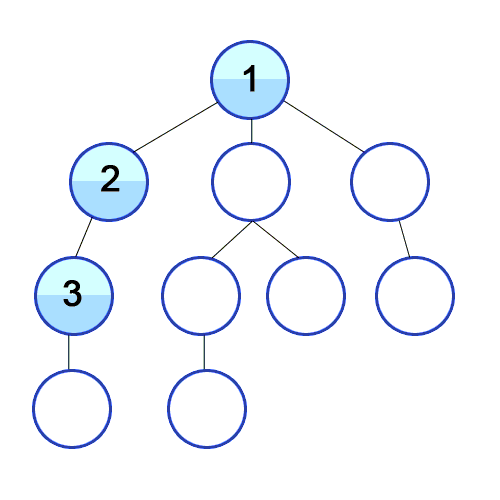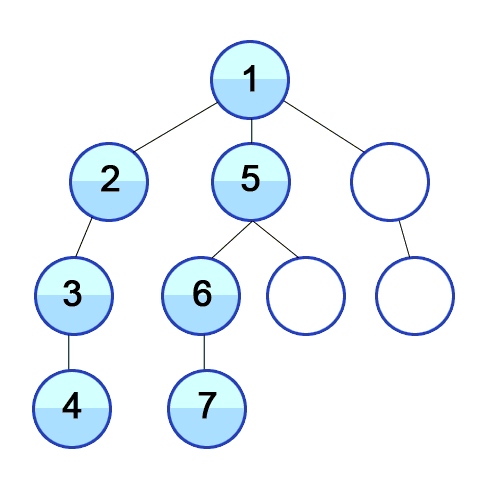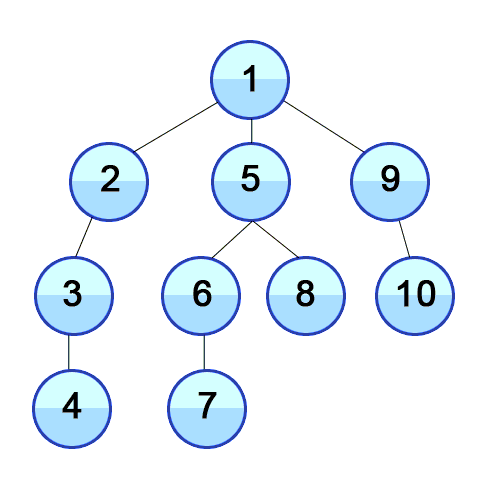
- 탐색할 수 있는 깊이까지 탐색해 리프 노드를 방문하고 이전 갈림길로 돌아가 선택하지 않은 다음 노드를 방문하는 식으로 탐색한다.
- 재귀를 사용하는데 dfs는 스택이고, 재귀함수 자체가 기본적으로 스택이기 때문에 재귀함수를 많이 사용한다.
- 코드의
graph는인접 리스트방식으로 저장되어 있다. - 인접 리스트(Adjacency List) 방식
- 모든 노드에 연결된 노드에 대한 정보를 차례대로 연결하여 저장하는 방식
작동방식
- 방문하는 노드마다
visited를True로 표시하며 탐색을 시작 graph에 노드마다 연결된 노드들이 있으므로for문으로 순회하며 방문하지 않은 노드들을 차례로dfs를 재귀 호출하며 방문
구현 예제
public class DFSTest {
// DFS 메서드 정의
public static void dfs(List<List<Integer>> graph, int v, boolean[] visited) {
visited[v] = true;
System.out.print(v + " ");
for (int i : graph.get(v)) {
if (!visited[i]) {
dfs(graph, i, visited);
}
}
}
public static void main(String[] args) {
// 그래프 초기화 (인접 리스트 방식)
int n = 6; // 노드 개수 (예제에 맞게 설정)
List<List<Integer>> graph = new ArrayList<>();
for (int i = 0; i <= n; i++) { // 0번 인덱스는 사용 안 함
graph.add(new ArrayList<>());
}
// 그래프 연결 정보 추가 (예제용)
graph.get(1).add(2);
graph.get(1).add(3);
graph.get(2).add(4);
graph.get(2).add(5);
graph.get(3).add(6);
boolean[] visited = new boolean[n + 1]; // 방문 여부 체크 배열
// 재귀함수로 DFS 수행
dfs(graph, 1, visited);
}
}
💡결론
DFS는 차례대로 정렬된 노드를 방문하며 그 인접 노드들을 재귀적으로 방문하는 것이다.
BFS (Breadth-First Search)
가까운 노드부터 탐색하는 알고리즘
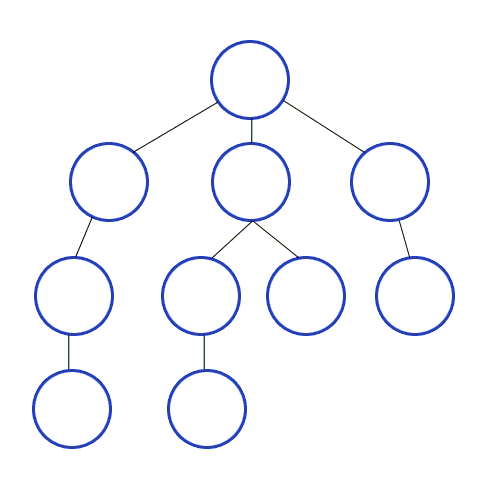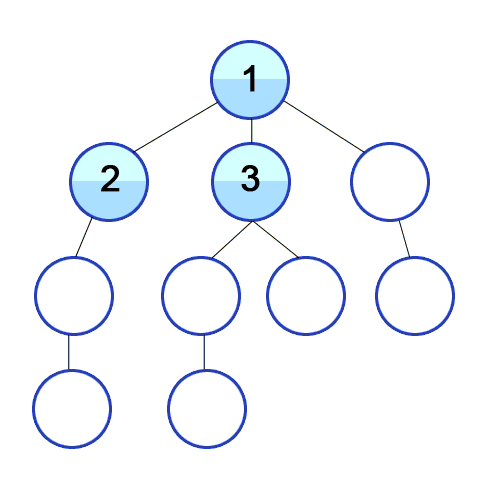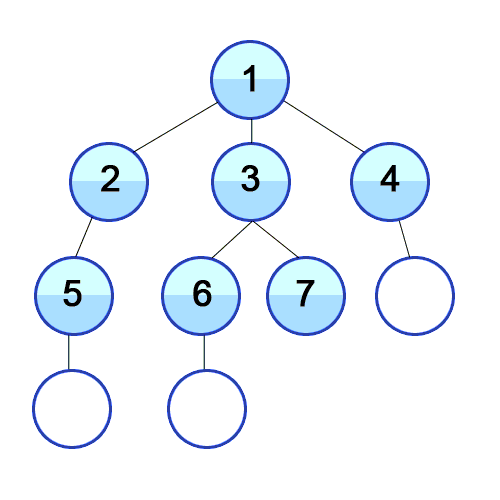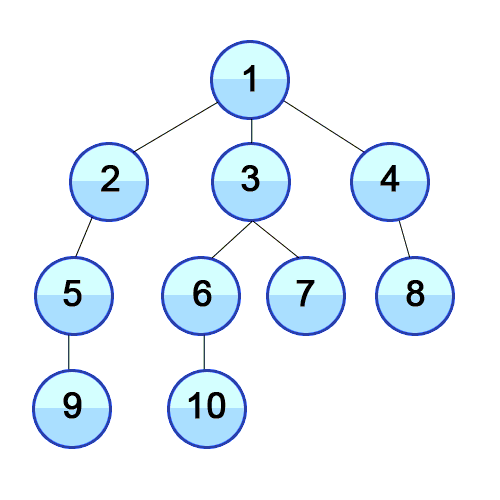
- 루트 노드와 같은 거리에 있는 제일 가까운 노드를 우선으로 방문하며 탐색한다.
- BFS는
queue자료구조를 이용하는 것이 일반적인데, 인접한 노드를 반복적으로 큐에 넣도록 알고리즘을 작성하면 자연스럽게 먼저 들어온 것이 먼저 나가게 되기 때문이다.
작동방식
- 탐색 시작 노드를
queue에 삽입 -> 방문 처리 queue에서 노드를 꺼내고 그 노드의 인접노드 중 방문하지 않은 노드를 모두queue에 삽입 → 방문처리- 전 과정을 수생할 수 없을 때까지 반복
예제
public class BFSTest {
// BFS 메서드 정의
public static void bfs(List<List<Integer>> graph, int start, boolean[] visited) {
Queue<Integer> queue = new LinkedList<>();
queue.add(start);
visited[start] = true;
while (!queue.isEmpty()) {
int v = queue.poll();
System.out.print(v + " ");
for (int i : graph.get(v)) {
if (!visited[i]) {
queue.add(i);
visited[i] = true;
}
}
}
}
public static void main(String[] args) {
int n = 6; // 노드 개수 (예제에 맞게 설정)
List<List<Integer>> graph = new ArrayList<>();
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<>());
}
// 그래프 연결 정보 추가 (예제용)
graph.get(1).add(2);
graph.get(1).add(3);
graph.get(2).add(4);
graph.get(2).add(5);
graph.get(3).add(6);
boolean[] visited = new boolean[n + 1];
// BFS 수행
bfs(graph, 1, visited);
}
}
💡결론
BFS는 차례대로 정렬된 노드를 큐에 넣고, 먼저 들어온 노드부터 순차적으로 방문하며 그 인접 노드들을 탐색하는 것이다.
시간 복잡도
| 알고리즘 | 시간 복잡도 (인접 리스트) | 시간 복잡도 (인접 행렬) | 공간 복잡도 |
|---|---|---|---|
| DFS | O(V+E) | O(V^2) | O(V) |
| BFS | O(V+E) | O(V^2) | O(V) |
그래프 알고리즘
그래프 알고리즘은 네트워크 분석, 경로 찾기 등 다양한 문제를 해결하는데 사용되는 중요한 알고리즘
그래프 기본 개념
- 그래프는 정점(Node or Vertex)과 이들을 연결하는 간선(Edge)으로 구성된 자료구조를 말한다.
- 방향성이 있는 방향 그래프와 방향성이 없는 무방향 그래프로 나뉘며, 간선에 가중치가 있을 수 있다.
그래프 구현 방법
그래프 구현 방법에는 인접 리스트를 사용하는 방법과 인접 행렬을 사용하는 방법이 있다.
1. 인접 리스트
- 인접 리스트는 각 정점에 대해 연결된 모든 정점의 리스트를 저장하는 방식이다
- 특정 정점과 인접한 정점들을 바로알 수 있다는 장점이 있다.
2. 인접 행렬
- 인접 행렬은 2차원 배열을 사용하여 노드 간의 연결 관계를 행렬 형태로 나타내는 방식이다.
- 노드 간의 연결 여부를 빠르게 확인할 수 있다는 장점이 있지만, 모든 각 정점에 관한 관계를 기록하기 때문에 메모리 소비가 크다.
💡따라서 인접 행렬은 그래프 간선이 많은 그래프에 주로 사용하고, 인접 리스트는 상대적으로 간선이 적은 그래프에서 주로 사용한다.
그래프 알고리즘의 종류
1. 그래프 탐색 알고리즘
- 그래프 탐색 알고리즘은 그래프에서 특정 정점을 찾는 알고리즘을 말한다.
- 그래프 내 특정 정점을 찾기 위해서는 그래프의 각 정점을 순회하면서 방문해야 하므로, 그래프 순회 알고리즘으로 부르기도 한다.
기본적인 그래프 탐색 알고리즘 종류에는 DFS(깊이 우선 탐색)와 BFS(너비 우선 탐색)이 있다.
2. 최단 경로 알고리즘
- 최단 경로 알고리즘은 가중치가 있는 그래프에서 두 정점간의 최소 가중치 합을 가지는 경로를 찾는 알고리즘을 말한다.
- 네트워크 설계, 교통 시스템 최적화, 지리적 경로 탐색 등에 사용된다.
대표적인 최단 경로 알고리즘에는 다익스트라 알고리즘, 벨만-포드 알고리즘, 플로이드 알고리즘 등이 있다.
3. 최소 신장 트리
- 최소 신장 트리 알고리즘은 그래프의 모든 정점을 최소한의 간선으로 연결하는 부분 그래프를 찾는 방식이다.
- 네트워크 설계, 클러스터링, 물리적 인프라 계획 등에서 중요한 역할을 한다.
대표적인 최소 신장 트리 알고리즘에는 크루스칼 알고리즘, 프림 알고리즘이 있다.
