Complexity

시간 복잡도란

시간이 아니라 연산 및 횟수가 얼만큼 걸리는지를 계산하는 것을 시간 복잡도라고 한다.

Big-o notation으로 가장 오랜 시간이 걸리거나 많은 공간을 사용해야하는 경우를 표기한다.
공간 표기는 잘 사용하지 않는다고한다.

- Time Complexity

Big-O-Notation : 가장 안좋은 알고리즘을 표기

• 숫자를 무시한다. (2n일 때는 n으로 표기한다.)
• 낮은 차수의 숫자는 없앤다. (n^2 +2n + 3을 n^2으로 표기한다.)
  
  
  
  

O(n^2) : Quadratic

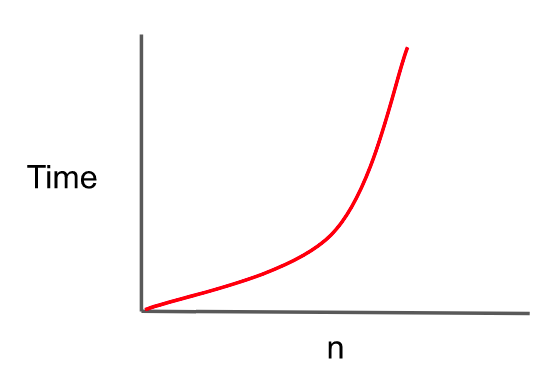Quadratic 예시

• 이중 반복문에서 해당하는 연산 횟수가 n * n일 때를 O(n^2)으로 표기한다.
• 연산하는 횟수가 기하급수적으로 늘어난다. 그래서 횟수가 하나씩 증가하면 배이상 늘어난다. 그만큼 시간이 오래 걸린다.
• 구구단 연산, 행렬 연산 등에서 사용하는 것 예로 들 수 있다.

for(i=0; i < N; i++) 
{
    for(j=0; j < N;j++)
    { 
    statement;
    }
}

O(n) : Linear

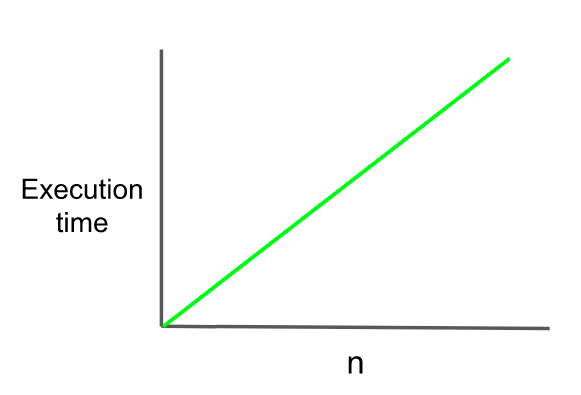Linear 예시

• 연산하는 횟수만큼 시간이 걸릴 때 사용하는 표기법이다. O(n)으로 표기하는데 반복문에서 연산할 때 시간 복잡도는 Linear 그래프를 따른다.
• 1 ~ 10까지를 출력할 때의 시간 복잡도가 O(n)이 되겠다.

for(i=0; i < N; i++)
{
    statement;
}

O(log n): Logarithmic

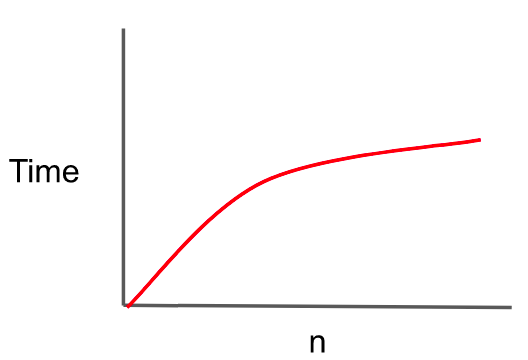Logarithmic

• 알고리즘의 실행 시간은 N을 2로 나눌 수 있는 횟수에 비례한다(N은 여기서 high, low).
• 연산하는데 반으로 나눠지는 연산을 O(log n) 표기법이라고 한다.
• binary search를 한 예로 들 수 있다. 아래 그림과 같이 binary search를 이용해서 6을 찾고자 할 때 1 ~ 10까지의 중간 값을 먼저 검색을 하고 찾고자 하는 값(6)보다 큰지 작은 지를 확인 한다. 확인 한 결과는 6보다 작으므로 5 밑으로는 검색할 필요가 없어진다. 그리고 6 ~ 10까지에서 중간값을 찾은 후에 비교한다. 중간값은 8이고 8보다 작으므로 8이상은 볼 필요가 없어진다. 남은 수는 6,7이고 찾고자하는 수와 비교하여 찾으면 끝이다. 이렇게 3번의 연산으로 시간이 확 줄었다. O(n)으로 작성한 알고리즘보다 훨씬 시간이 줄어드는 것을 알 수 있다.
  
  
  

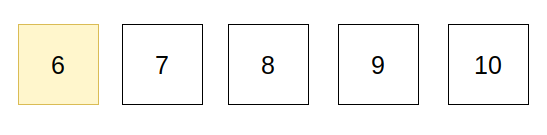
while(low <= high) 
{
    mid = (low + high) / 2;
    if (target < list[mid])
        high = mid - 1;
    else if (target > list[mid])
        low = mid + 1;
    else break;
}

O(1) : constant

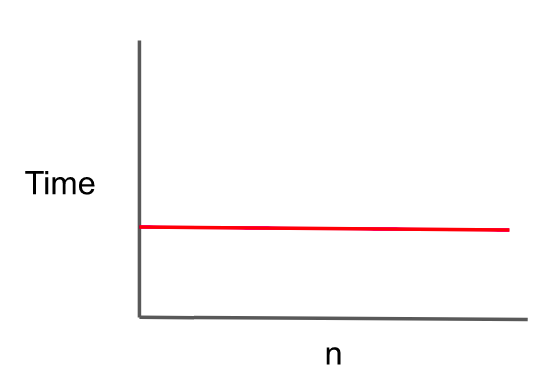• constant notation은 데이터의 양이 많아도 한번만 연산하는 시간 복잡도를 표기한다.
• 한 예로 배열에서 특정 인덱스를 조회하고 싶을 때 시간복잡도는 O(1)이다.

시간 복잡도 빠른 순서
O(1) > O(log n) > O(n) > O(n^2) > O(2^n) 순으로 시간복잡도가 오래 걸린다.