Bloch Sphere

Qubit

Quantum system of 2 level orthogonal states = qubit.

qubit 은 trapped ion 처럼 원자를 이용해서 구현할 수도 있고, 빛의 편광같은 optical system 을 이용해 구현할 수도 있다.

양자적으로 구분되는 two level system 이면 qubit 이 될 수 있다.

Bloch Sphere

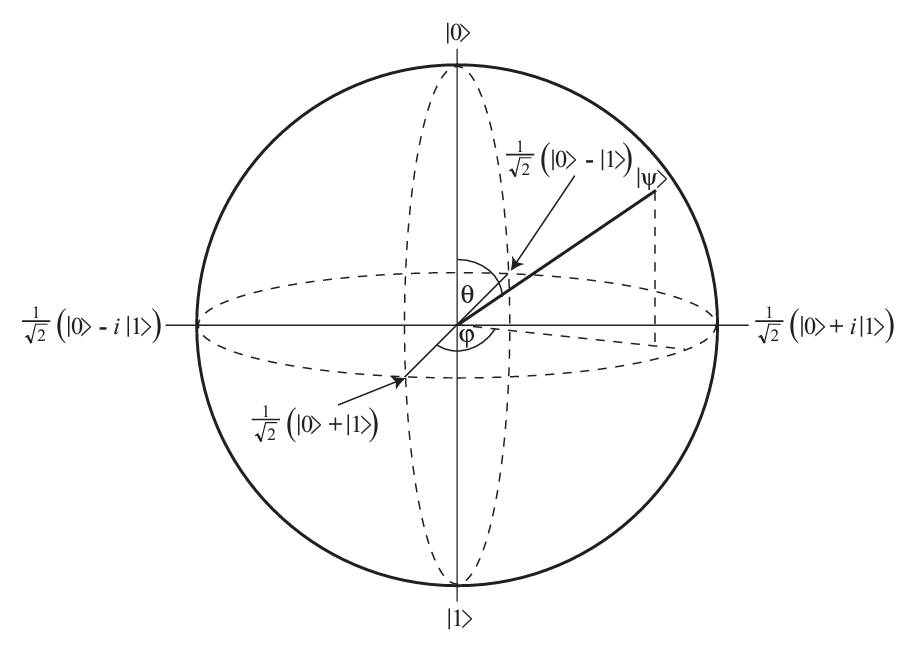
qubit 을 기하학적으로 표현하는 방법.

파울리 행렬 $\sigma_{x},\sigma_{y},\sigma_{z}$의 eigenstate인
$\frac{1}{\sqrt{2}} (\ket{0}\pm\ket{1}),\frac{1}{\sqrt{2}} (\ket{0}\pm i\ket{1}), \ket{0} and \ket{1}$을 각각 x축, y축, z축으로 하는 구를 그린다.

pure state 는 Bloch sphere 의 표면에 위치하고, mixed state는 스피어 내부에 위치한다.

임의의 pure state 는 다음과 같이 쓸 수 있다.

How?

임의의 양자 상태 $\ket{\psi} = \alpha\ket{0} + \beta e^{i\phi}\ket{1}$에 대해서 ($e^{i\phi}$는 phase factor) normalize 조건에 의해 두 coefficient 의 제곱의 합은 1이다.

polar coordinate 에서 $z=re^{i\phi}$ 로 표현할 수 있으므로, $\beta e^{i\phi} = x+iy$ 로 쓸 수 있고, $\alpha^{2} + (x+iy)(x-iy) = 1$ 이므로 3차원 구면좌표계는 $(x,y,\alpha)$로 표현할 수 있다.

이때 $x=r\sin{\theta}\cos{\phi}, y=r\sin{\theta}\sin{\phi}, z=r\cos{\theta}$ 이고 r=1 이라 한다면 임의의 양자상태 $\ket{\psi}$ 는 다음과 같다.

이때 xy plane 위쪽 반구의 임의의 점 $(1, \theta, \phi)$ 를 원점대칭한 $(1, \pi-\theta, \pi+\phi)$의 경우, 기존 벡터에서 phase factor -1 만 붙은 동일한 벡터임을 알 수 있다.

위쪽 반구와 아랫쪽 반구가 동일한 정보를 갖고 있으니, 위쪽 반구만 사용. $\theta = 2\theta'$인 $\theta'$ 공간에서 임의의 양자상태를 표현한다면

이고, 여기서 $\theta'$ 를 $\theta$ 로 쓴다면

이다.