Regressions

Linear Regression

데이터 분포가 주어졌을때, 해당 데이터와 가까운 1차식 y=Wx + b 를 찾기.

이때 loss function : 분산(데이터값과 수식값의 차이의 제곱을 다 더하고 평균내기)

Logistic Regression

true or false 를 판별하는 상황 -> 데이터와 잘 맞는 Sigmoid function 을 찾기.

loss function 은 log 함수를 이용. log 함수의 특성: 0과 1근처에서는 값이 급변, 그러나 중간(0.5)는 값의 변화가 완만. -> true(1) or false(0) 를 판별하는 문제이기에 0과 1 근처에서 오차값이 급변하는 log 함수를 loss function 으로 쓰는게 괜찮은 결과가 나옴.

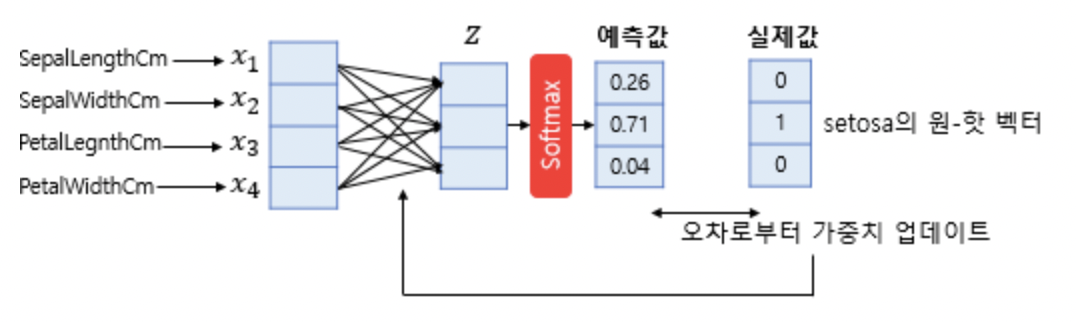
Softmax Regression

무언가를 여러 클래스로 분류하는 상황(Multi-Class Classification).

각 클래스에 정수 인덱스 대신 벡터로 인덱싱.

소 = (1,0,0)
돼지 = (0,1,0)
닭 = (0,0,1)

정수로 인덱싱을 하면, 예를 들어 소=0, 돼지=1, 닭=2 이런식으로 하면, 분류간의 거리(소-닭은 2, 돼지-소는 1)가 각각 달라진다. 각 레이블간 거리를 같게 하기 위해 n 차원 벡터를 인덱스로 부여해줌.

총 k개의 인덱스가 있을때, 인풋이 i 번째 클래스에 속할 확률은 다음과 같다.

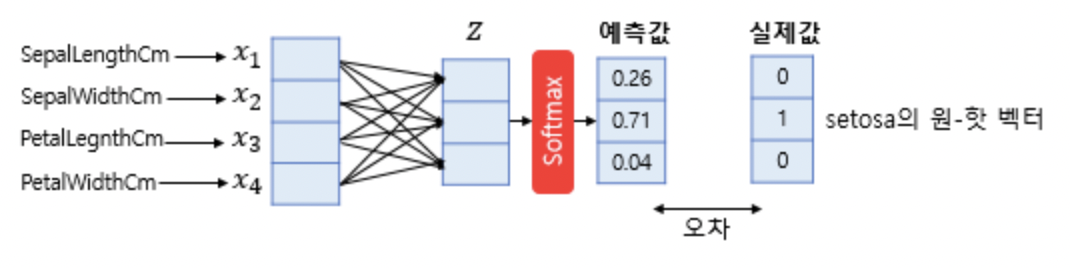
m개의 파라미터에 가중치 w를 곱해서 k개로 분류. 가중치 행렬은 m * k 행렬이 된다.