문제

나는 해당 문제에 대해서 처음에 단순한 DFS 문제로 접근했다. 그 이유는 다음과 같다.
- N x M 의 최댓값이 500 * 500 이므로 250,000 이다.
- 항상 내리막길로 가야한다는 조건 때문에 항상 모든 장소를 탐색하지 않아도 된다. 즉, 탐색에 있어 많은 제한이 있을 것으로 판단했다.
이러한 이유로 단순 DFS 풀이와 setrecursionlimit를 10 ** 6 까지만 해제하여(최대 250,000 이므로) 재귀를 마음껏 진행할 수 있도록 하였지만, 시간초과와 마주했다. 도대체 어떻게 최적화해야 이 문제를 해결할 수 있을까 고민했다. 그래서 모든 거리 관련 알고리즘을 떠올렸다.
- BFS로 풀어야 하나? -> 이 문제는 경로의 경우의 수를 구해야하기 때문에 적절하지 않다.
- 다익스트라로 풀어야 하나? -> 최단 거리와는 상관없다. 도달하기만 하면 된다.
- Kruskal, Prim -> 최소 신장 트리와는 관련이 없다.
도저히 아이디어가 떠오르지 않아서 해당 문제와 관련된 블로그를 많이 찾아보았다. 정답은 DFS와 DP 개념을 결합하여 불필요한 탐색 수를 줄여 경우의 수를 구하는 방법이 해결법이었다. DP 개념이 그래프와도 결합될 수 있다는 점에 놀라웠다.
아이디어
DFS 와 DP 결합 아이디어는 다음과 같다.
- dp 테이블을 -1(방문하지 않은 상태)로 초기화한다.
- 일반적인 DFS를 조건에 맞추어 구현한다.
- (n - 1, m - 1) 위치에 도달하면 1을 return한다.
- 그러면 다시 역추적하면서 dp[y][x]에 return 값을 저장한다.
- 만약, 나아가다가 -1이 아닌 정점과 마주하면, 이미 그 길은 방문했다는 의미로 해당 숫자를 return한다.
- 이 과정을 모두 수행하면 (0, 0)에 (n - 1, m - 1)까지 가는 경우의 수가 저장되어있다.
- 즉, dp[y][x]는 (y, x) -> (n - 1, m - 1) 갈 수 있는 경우의 수이다.
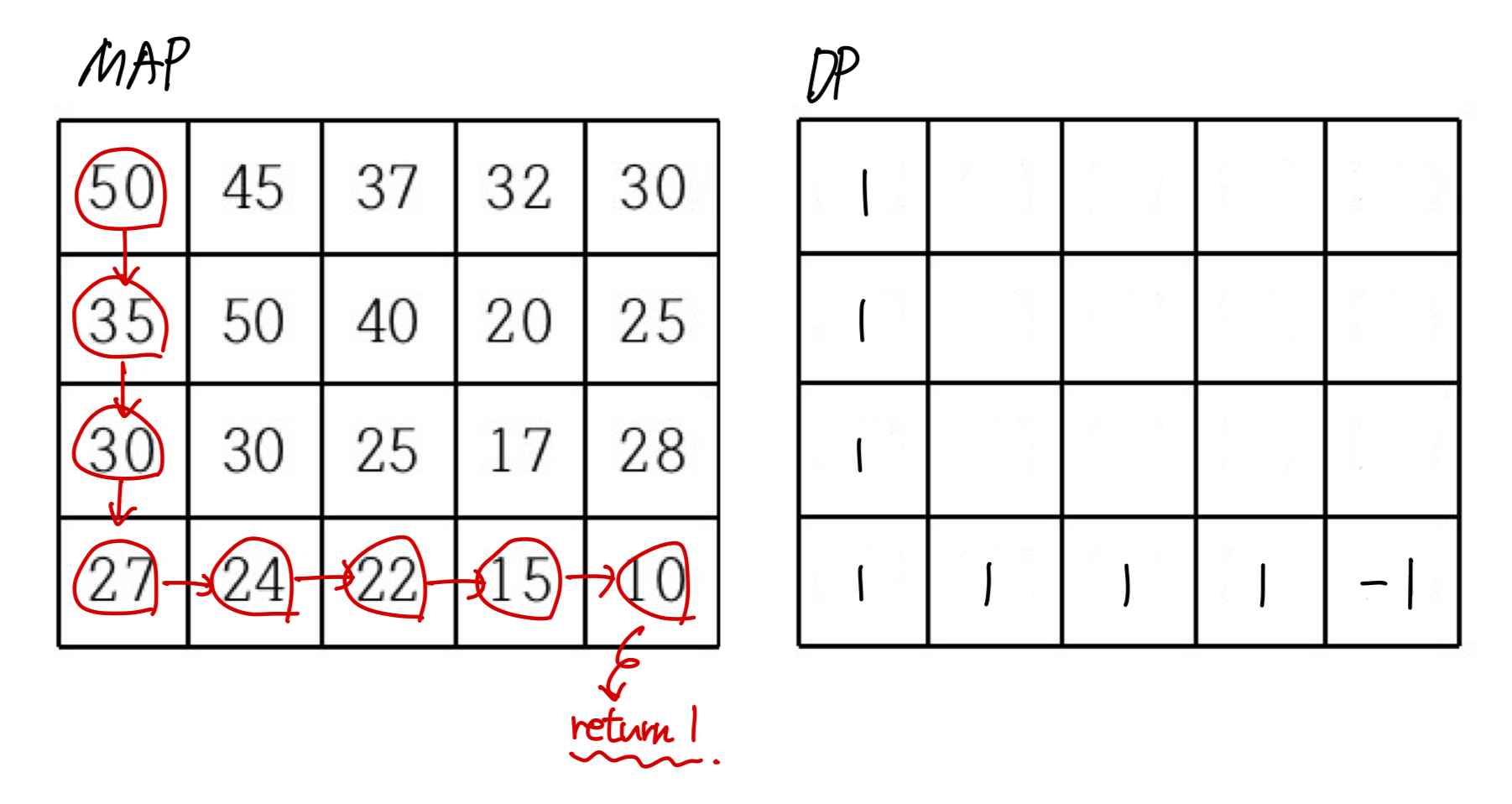
-> 처음 DFS를 통해서 내리막길 조건을 만족하면서 목적지까지 갑니다.
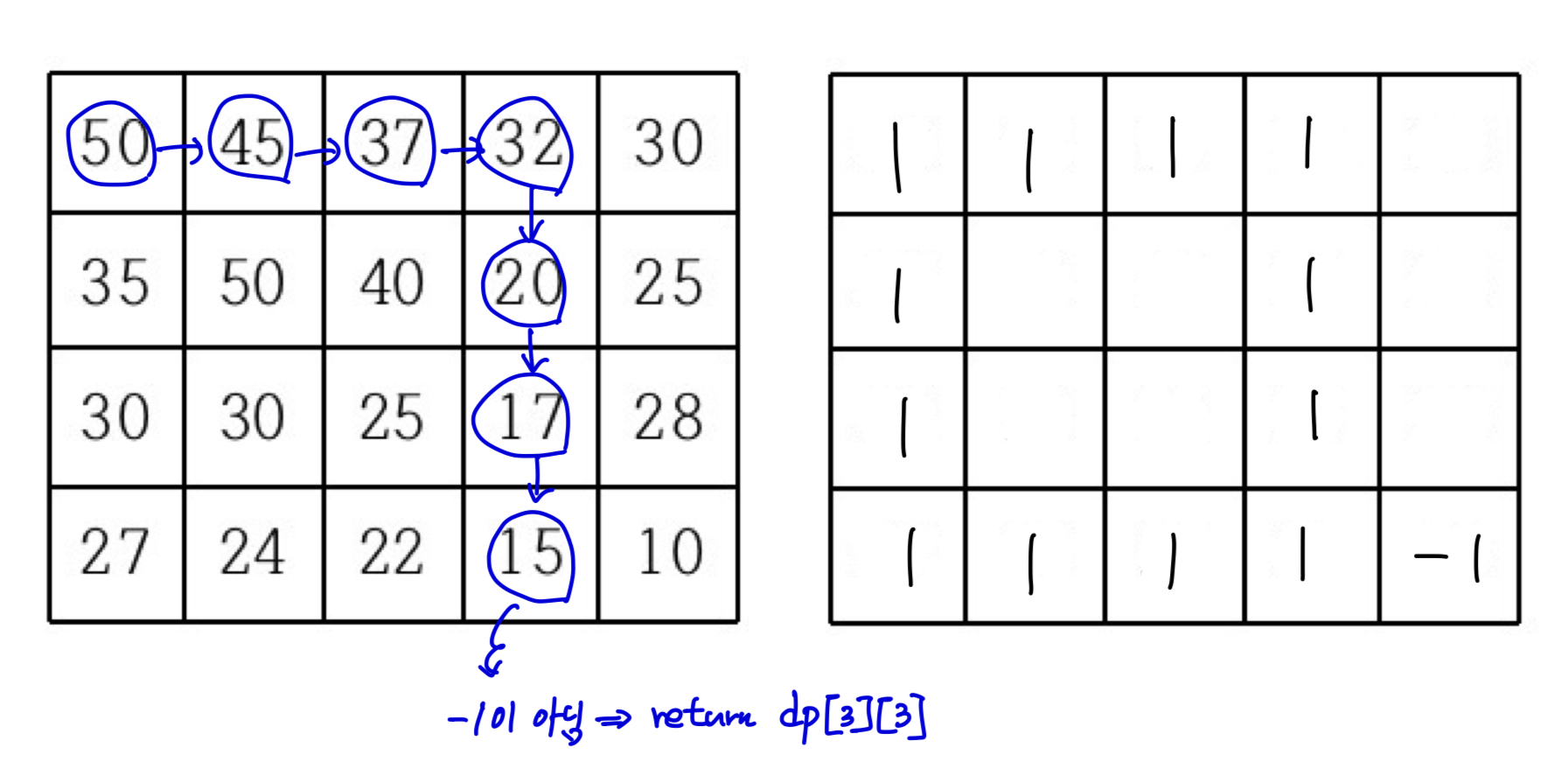
-> 만족하는 조건이 없어 DFS를 복귀하고, 다시 다른 가지로 뻗어나갑니다. 뻗어나가는 도중에 이미 방문했던 정점을 만났다면, 이미 방문한 정점이 가지고 있는 숫자를 return 합니다. 그 숫자를 현재 경로까지의 방법 수를 더해줍니다.
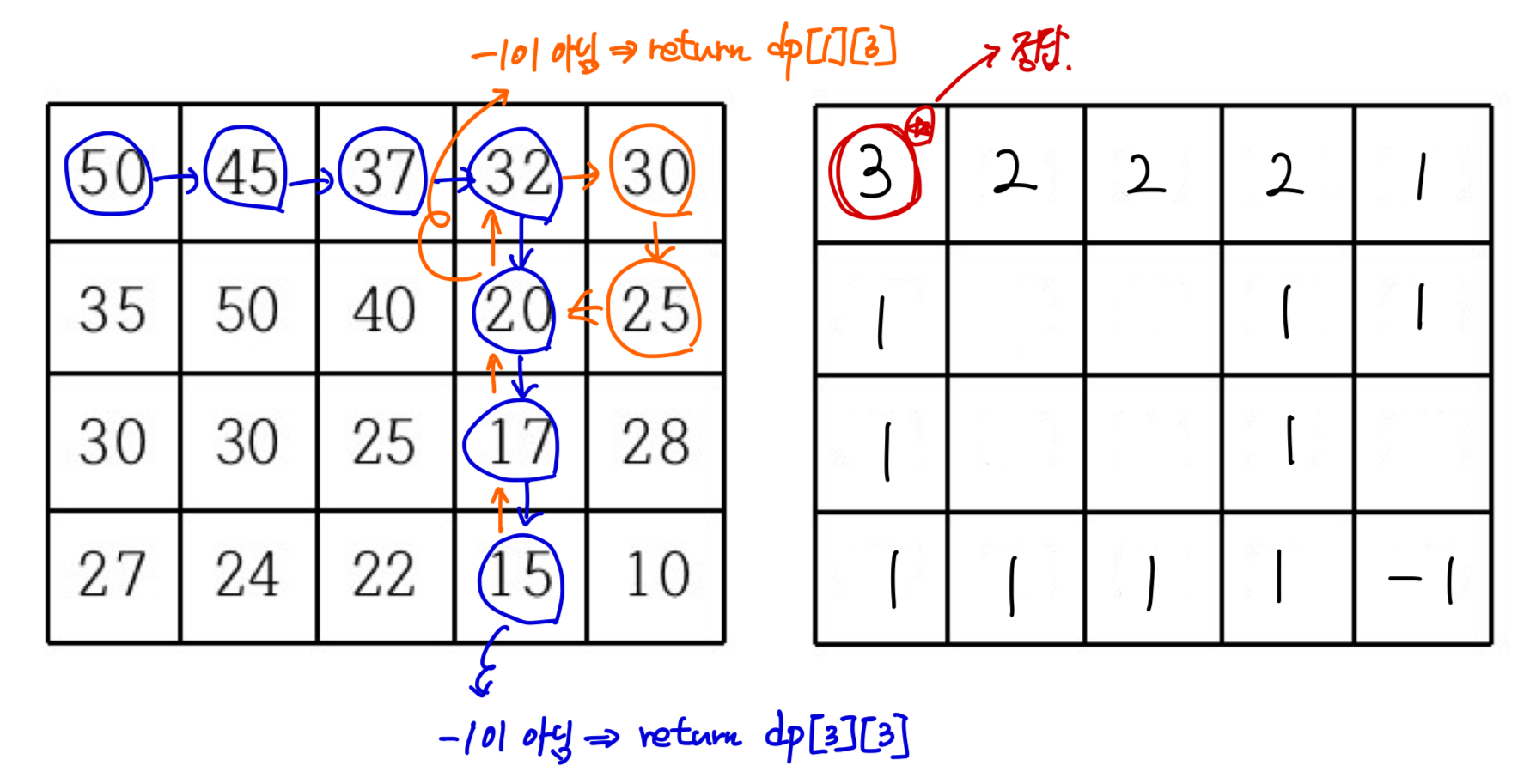
-> 마찬가지로, 만족하는 조건이 없어 복귀하다가 다시 뻗어나갑니다. 32 -> 30 -> 25 -> 20 에서 이미 방문했던 20을 만났고, 해당 값인 1을 return 합니다. return 하면서 현재 경로까지의 방법 수를 더해주면서 dp값을 최신화합니다. 이와 같은 과정을 통해서 dp[0][0]까지 초기화가 진행되고, 이 값이 정답이 됩니다.
파이썬 코드
from sys import stdin, setrecursionlimit
setrecursionlimit(10 ** 6)
input = stdin.readline
def dfs(cur_y, cur_x):
# 도착 지점에 도달하면 1(한 가지 경우의 수)를 리턴
if cur_y == n - 1 and cur_x == m - 1:
return 1
# 이미 방문한 적이 있다면 그 위치에서 출발하는 경우의 수를 리턴
if dp[cur_y][cur_x] != -1:
return dp[cur_y][cur_x]
ways = 0
for dy, dx in zip(dys, dxs):
nxt_y, nxt_x = cur_y + dy, cur_x + dx
if 0 <= nxt_y < n and 0 <= nxt_x < m and MAP[cur_y][cur_x] > MAP[nxt_y][nxt_x]:
ways += dfs(nxt_y, nxt_x)
dp[cur_y][cur_x] = ways
return dp[cur_y][cur_x]
n, m = map(int, input().split())
MAP = [list(map(int, input().split())) for _ in range(n)]
dp = [[-1] * m for _ in range(n)]
dys, dxs = [1, -1, 0, 0], [0, 0, 1, -1]
print(dfs(0, 0))
-> 구현 코드는 위와 같습니다. Pypy3는 메모리를 더 잡아먹기 때문에 메모리 초과 결과를 받습니다. 따라서, Python3로 제출하시면 정답 판정을 받을 수 있습니다.
