[백준 2146] 다리 만들기 (Python)

김용범·2024년 12월 10일

백준 코딩테스트

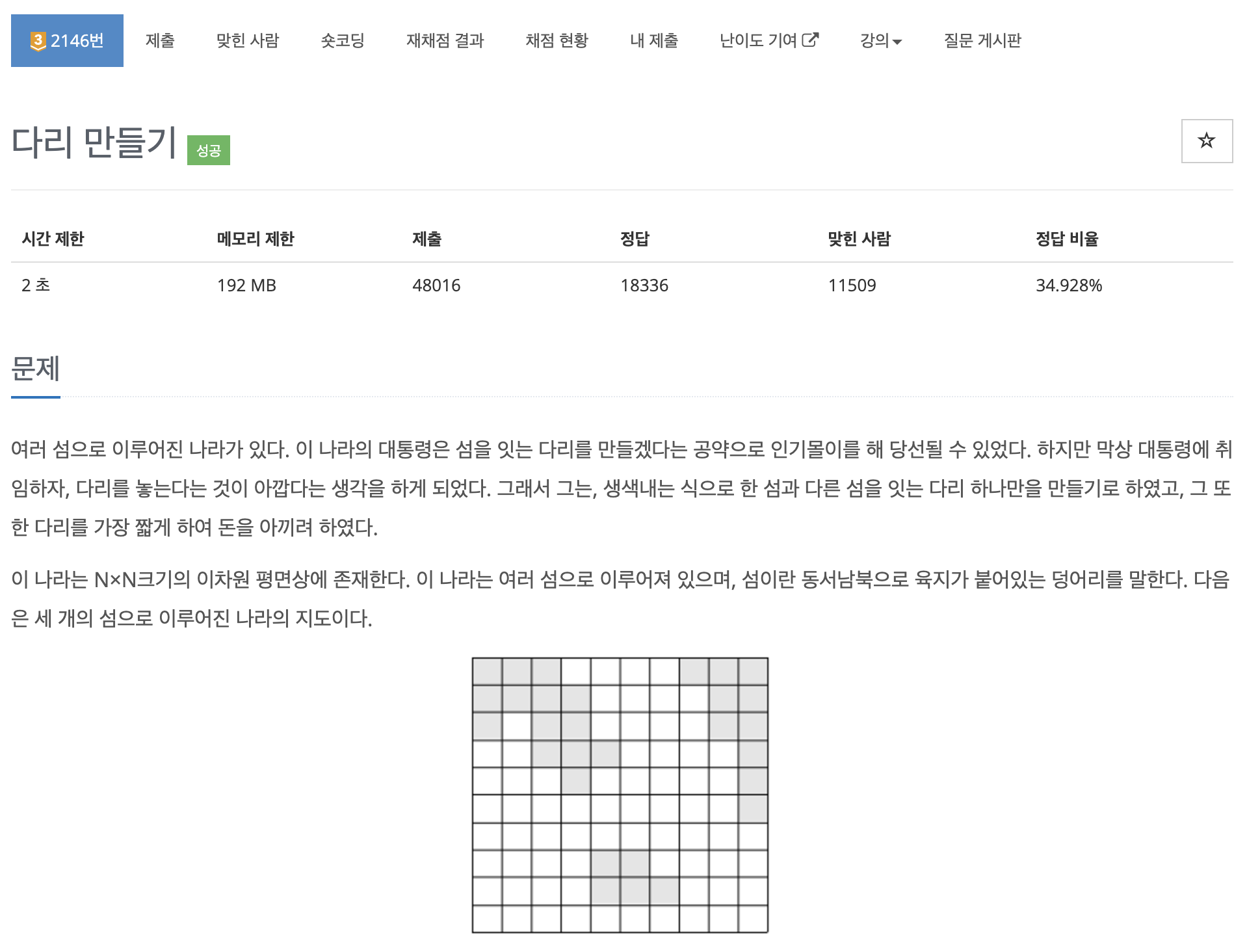
문제 💁🏻‍♂️

문제 링크 - 백준 2146 다리 만들기

해결 과정

문제를 보고 가장 먼저 든 아이디어는 아무래도 각 대륙 간 가장 짧은 다리의 길이를 구하는 문제이기 때문에 그래프 최단 거리 그리고 최소 신장 트리이다.

1) 그래프 최단 거리
[ 근거 ] 그냥 "가장 짧은 다리의 길이 == 최단 거리"로 생각했고, 가중치가 따로 주어지지 않기 때문에 BFS로 문제를 풀이하면 깔끔하겠다는 생강기 들었다.

2) 최소 신장 트리(MST)
[ 근거 ] 뭔가 육지라는 하나의 집합으로 하여 각 육지를 연결해야하나 ? 라는 생각이 들어서 최소 신장 트리가 떠올랐다.

결과적으로는 그저 육지 간 짧은 거리를 구하면 되겠구나 생각해서 1번 그래프 최단 거리 아이디어로 밀고 가기로 마음 먹었다.

사고 과정 (1) ❗️

최단 거리를 사용해서 풀기 위해서 어떻게 접근해야할까? 나는 이렇게 생각을 했다.

각 육지를 구분해야하고, 어느 한 육지에서 시작했으면 시작했던 육지는 탐색에서 제외해야겠다.
육지의 내부에서는 굳이 탐색할 필요는 없겠구나. 그러면 바다와 맞닿아있는 육지의 외곽 부분에서만 탐색을 해야겠다.

이를 구현하기 위해서 edges 라는 리스트를 만들고, 입력을 모두 받은 다음에 완전 탐색을 하면서 1인 육지에서 상, 하, 좌, 우를 탐색했을 때, 0값이 하나라도 있다면 edges 리스트에 해당 위치를 추가하였다. (N <= 100 이기 때문에 완전 탐색을 하여 외곽 부분을 담아도 상관 없겠다는 판단)

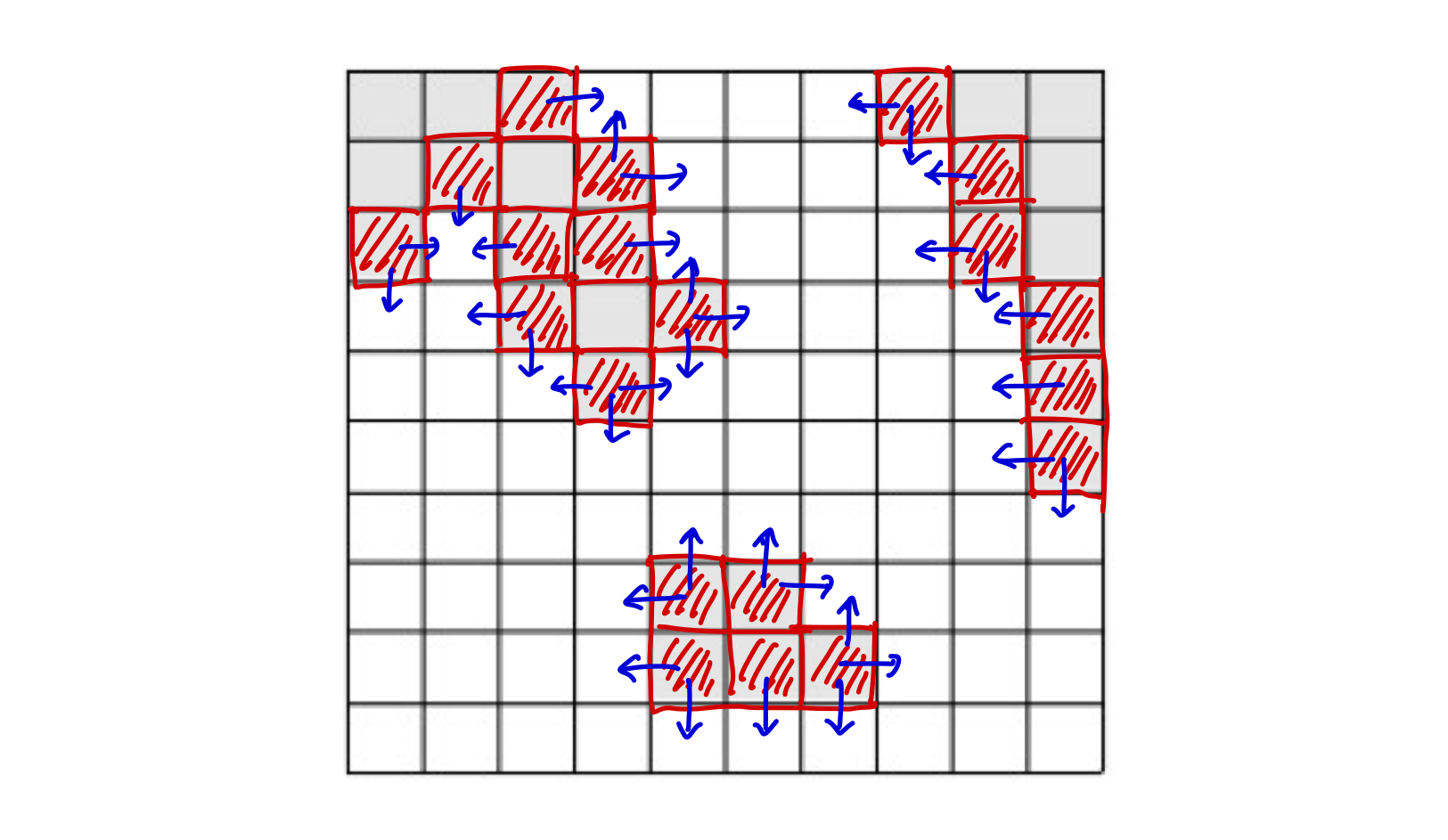
(위 그림은 edges 리스트에 담길 육지의 외곽 위치들입니다.)

여기까지 구현을 하고 난 뒤에

edges 리스트를 돌면서 다른 육지까지의 최단 거리를 BFS 알고리즘을 통해서 전역 최솟값을 갱신하자.
육지를 구분하기 위해서 edges에서 값을 꺼낼 때마다, visited 리스트를 갱신하고, 해당 위치에서 DFS 알고리즘을 활용해서 현재 육지의 모든 위치를 방문 처리한다.
결과적으로 현재 육지에 대해서는 모두 방문처리를 해줬기 때문에, 방문하지 않은 1값을 가진 다른 육지까지의 거리를 구할 수 있다.

이렇게 BFS와 DFS 알고리즘을 모두 사용하여 구현을 하고, 제출해보니 정답 판정을 받을 수 있었다. 그러나, 3740ms 를 받고 통과한 것이 맘에 들지 않았다.

사고 과정 (2) ‼️

시간이 너무 오래 걸렸지만, 통과한 것이 맘에 들지 않아 코드를 유심히 살펴보았다. 논리적으로는 문제가 없어보였지만, 불필요한 연산을 하고 있는 부분을 발견했다.

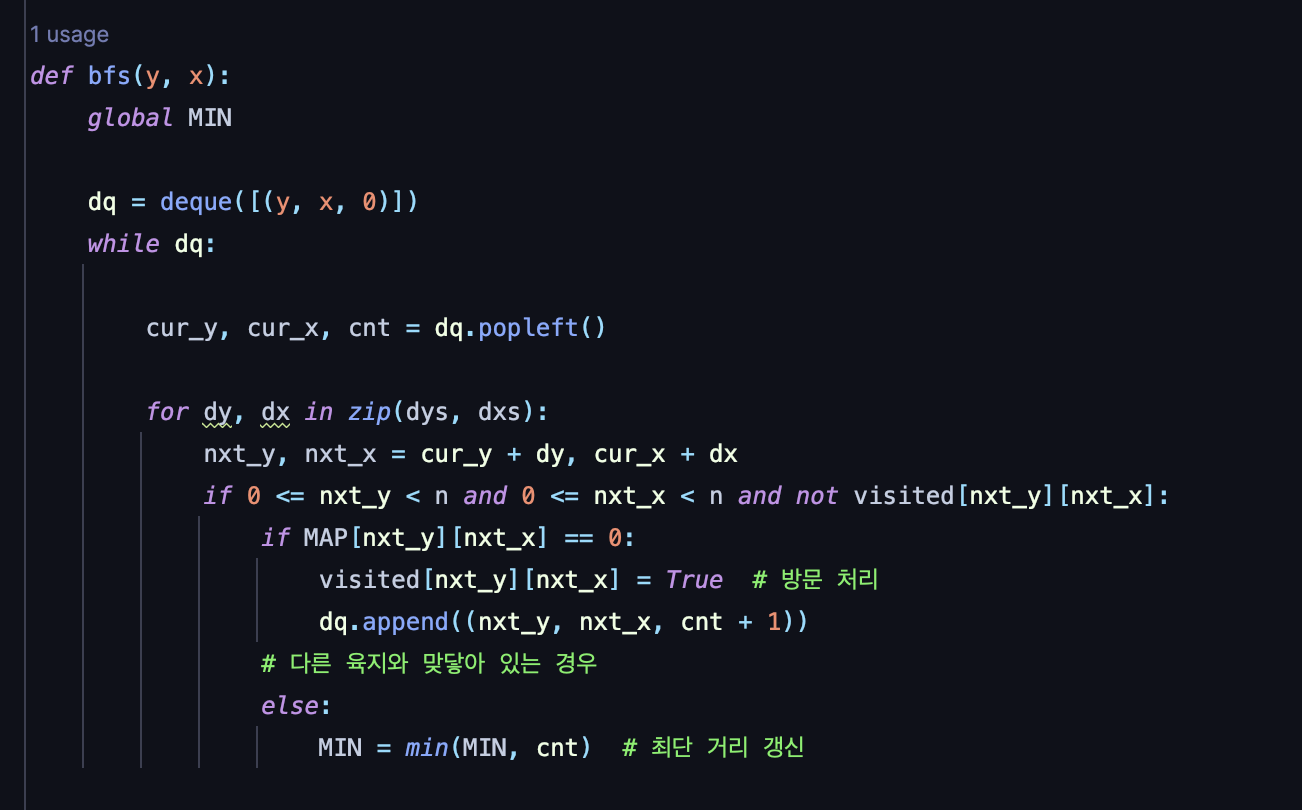
BFS 알고리즘 부분에서 전역 최솟값인 MIN값을 갱신하고 난 이후의 연산은 불필요하다는 것을 확인했다. 그 이유는 바로 BFS 특성 때문이다. BFS 알고리즘은 너비 우선 탐색으로 만약 가장 먼저 최솟값이 갱신이 되었다면, 그 뒤의 최솟값들은 갱신된 최솟값보다 같거나 큰 값이다. 따라서 한번 갱신이 되었다면, 곧바로 return 해주면 된다. 그 결과 3740ms -> 672ms 로 시간을 단축할 수 있었다!

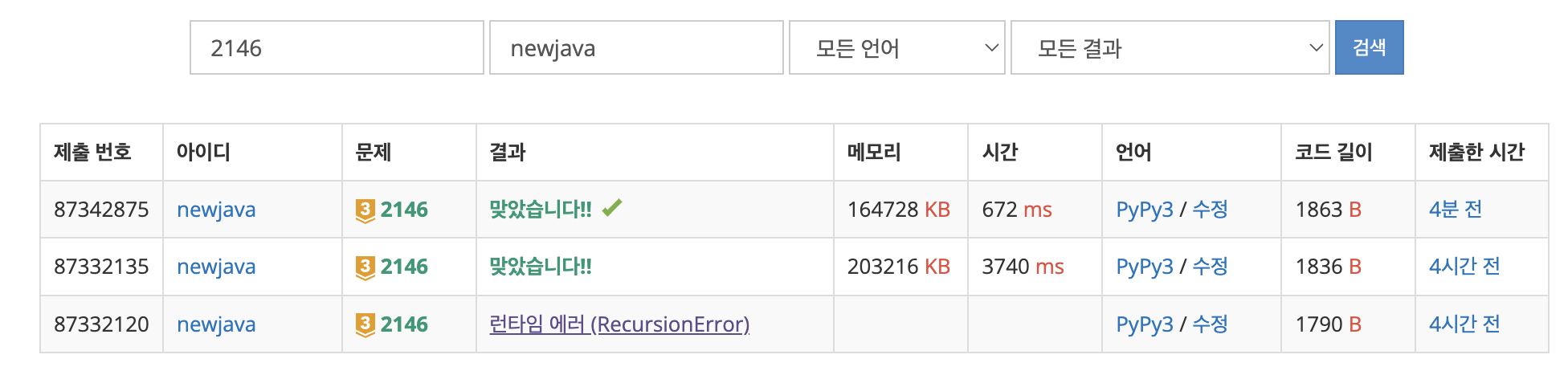
(런타임 에러 결과는 setrecursionlimit 설정을 해주지 않아 발생했다.)

코드

정답 풀이

from sys import stdin, setrecursionlimit
from collections import deque

setrecursionlimit(10 ** 4)
input = stdin.readline


def dfs(cur_y, cur_x):
    for dy, dx in zip(dys, dxs):
        nxt_y, nxt_x = cur_y + dy, cur_x + dx
        if 0 <= nxt_y < n and 0 <= nxt_x < n and not visited[nxt_y][nxt_x] and MAP[nxt_y][nxt_x] == 1:
            visited[nxt_y][nxt_x] = True  # 방문 처리
            dfs(nxt_y, nxt_x)


def bfs(y, x):
    global MIN

    dq = deque([(y, x, 0)])
    while dq:

        cur_y, cur_x, cnt = dq.popleft()

        for dy, dx in zip(dys, dxs):
            nxt_y, nxt_x = cur_y + dy, cur_x + dx
            if 0 <= nxt_y < n and 0 <= nxt_x < n and not visited[nxt_y][nxt_x]:
                if MAP[nxt_y][nxt_x] == 0:
                    visited[nxt_y][nxt_x] = True  # 방문 처리
                    dq.append((nxt_y, nxt_x, cnt + 1))
                # 다른 육지와 맞닿아 있는 경우
                else:
                    MIN = min(MIN, cnt)  # 최단 거리 갱신


n = int(input().rstrip())
# 0: 바다 / 1: 육지
MAP = [list(map(int, input().split())) for _ in range(n)]
edges = []
dys, dxs = [-1, 1, 0, 0], [0, 0, -1, 1]

for i in range(n):
    for j in range(n):
        # 육지인 경우
        if MAP[i][j] == 1:
            flag = False
            for dy, dx in zip(dys, dxs):
                ny, nx = i + dy, j + dx
                if 0 <= ny < n and 0 <= nx < n:
                    if MAP[ny][nx] == 0:
                        flag = True

            # 육지의 가장자리인 경우
            if flag:
                edges.append((i, j))

MIN = float('inf')
for ey, ex in edges:
    visited = [[False for _ in range(n)] for _ in range(n)]
    visited[ey][ex] = True  # 방문 처리
    dfs(ey, ex)  # 같은 육지는 모두 방문 처리
    bfs(ey, ex)

print(MIN)

정답 최적화 풀이

from sys import stdin, setrecursionlimit
from collections import deque

setrecursionlimit(10 ** 4)
input = stdin.readline


def dfs(cur_y, cur_x):
    for dy, dx in zip(dys, dxs):
        nxt_y, nxt_x = cur_y + dy, cur_x + dx
        if 0 <= nxt_y < n and 0 <= nxt_x < n and not visited[nxt_y][nxt_x] and MAP[nxt_y][nxt_x] == 1:
            visited[nxt_y][nxt_x] = True  # 방문 처리
            dfs(nxt_y, nxt_x)


def bfs(y, x):
    global MIN

    dq = deque([(y, x, 0)])
    while dq:

        cur_y, cur_x, cnt = dq.popleft()

        for dy, dx in zip(dys, dxs):
            nxt_y, nxt_x = cur_y + dy, cur_x + dx
            if 0 <= nxt_y < n and 0 <= nxt_x < n and not visited[nxt_y][nxt_x]:
                if MAP[nxt_y][nxt_x] == 0:
                    visited[nxt_y][nxt_x] = True  # 방문 처리
                    dq.append((nxt_y, nxt_x, cnt + 1))
                # 다른 육지와 맞닿아 있는 경우
                else:
                    MIN = min(MIN, cnt)  # 최단 거리 갱신
                    return 

n = int(input().rstrip())
# 0: 바다 / 1: 육지
MAP = [list(map(int, input().split())) for _ in range(n)]
edges = []
dys, dxs = [-1, 1, 0, 0], [0, 0, -1, 1]

for i in range(n):
    for j in range(n):
        # 육지인 경우
        if MAP[i][j] == 1:
            flag = False
            for dy, dx in zip(dys, dxs):
                ny, nx = i + dy, j + dx
                if 0 <= ny < n and 0 <= nx < n:
                    if MAP[ny][nx] == 0:
                        flag = True

            # 육지의 가장자리인 경우
            if flag:
                edges.append((i, j))

MIN = float('inf')
for ey, ex in edges:
    visited = [[False for _ in range(n)] for _ in range(n)]
    visited[ey][ex] = True  # 방문 처리
    dfs(ey, ex)  # 같은 육지는 모두 방문 처리
    bfs(ey, ex)

print(MIN)