처음
이번에는 "빡구현"이라고 불리는 시뮬레이션, 구현에 대해서 공부했다. 시뮬레이션은 정형화된 방식의 풀이 방법이 있지 않은 문제들을 말한다. 그래서 지금까지 공부했던 알고리즘이나 자료구조들과는 달리 필요한 추가적인 배경지식이랄 것이 없다고 할 수 있다. 시뮬레이션 문제들에 대한 감을 잡고, 그들의 특징에는 어떤 것이 있을 지 연습 문제들을 풀면서 알아보자.
중간
1. 백준 15683 - 감시
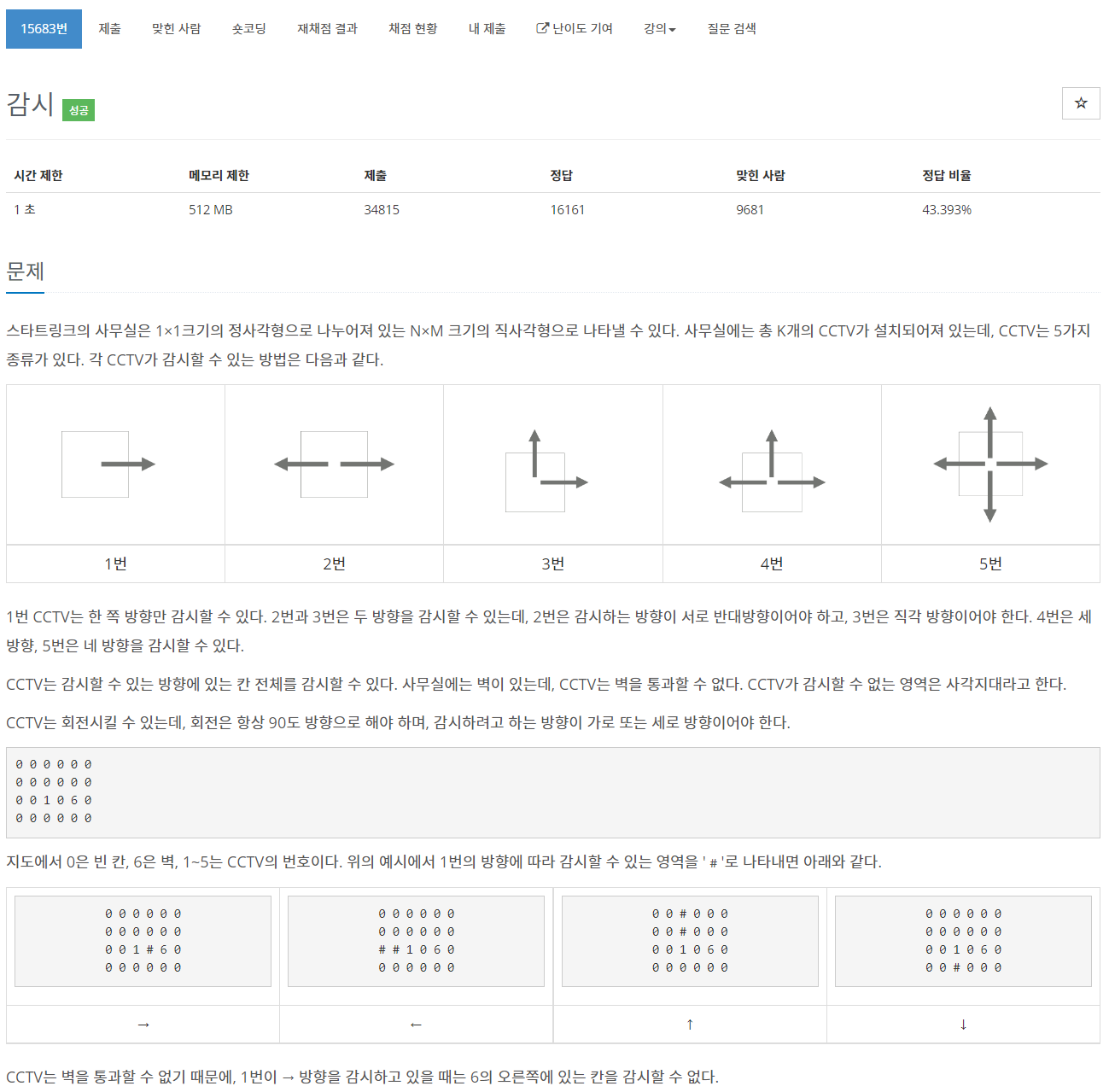
처음으로 접한 시뮬레이션 문제였는데, 끝나질 않는 스크롤을 보면서 이것이 시뮬레이션인가 하는 선입견을 갖게 됐다.
문제를 요약해보자면 이렇다.
- 다섯 가지 종류의 cctv가 사무실에 존재하고, 이것은 상하좌우 회전이 가능하다.
- cctv의 감시 범위는 벽을 만나기 직전까지이고, 다른 cctv는 통과할 수 있다.
위 정보를 바탕으로 최소 사각지대의 크기를 구하는 것이다.
처음에는 cctv 방향의 모든 경우의 수를 확인하지 않는 방법을 생각하려 했는데, 사무실의 최대크기도 8*8이었고, cctv도 최대 7개이므로 네 방향으로 모두 돌릴 수 있는 1, 3, 4번 카메라로만 구성되어있다고 해도 4^7, 약 8000번의 검사밖에는 필요하지 않았다. 내가 해결한 방식은 다음과 같다.
- 모든 cctv 방향 경우의 수에 대해서 검사
1-1. 각 경우에 cctv가 cover하는 감시 범위 계산 - tmpSum, 지금까지 경우 중 최대값과 비교
1-1-2. 더 크다면, 대체
1-2. 감시범위 최댓값+벽 개수+cctv 개수를 n*m에서 빼서 반환
package simulation;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.StringTokenizer;
//진법 활용해서 독립적인 변수들의 경우의수 구하는 방법 기억하기!!!
class Cctv {
int x;
int y;
public Cctv(int x, int y) {
this.x = x;
this.y = y;
}
}
public class BOJ15683 {
static int[][] board;
static List<Cctv> cctvs = new ArrayList<>();
static int[] dx = {1, 0, -1, 0};
static int[] dy = {0, 1, 0, -1};
static boolean[][] monitored;
static int n;
static int m;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
int wallsN = 0;
board = new int[n][m];
for (int i = 0; i < n; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < m; j++) {
int tmp = Integer.parseInt(st.nextToken());
if (tmp == 6) wallsN++;
if (tmp != 0 && tmp != 6) cctvs.add(new Cctv(i, j));
board[i][j] = tmp;
}
}
int[] directions = new int[cctvs.size()];
int caseNum = (int) Math.pow(4, cctvs.size());
int max = 0;
for (int i = 0; i < caseNum; i++) {
fourJinsu(directions, i);
int tmpSum = 0;
monitored = new boolean[n][m];
for (int j = 0; j < directions.length; j++) {
Cctv tmp = cctvs.get(j);
int tmpDir = directions[j];
switch (board[tmp.x][tmp.y]) {
case 1:
tmpSum += monitor(tmp.x, tmp.y, tmpDir);
continue;
case 2:
if (tmpDir % 2 == 0) {
tmpSum += monitor(tmp.x, tmp.y, 0);
tmpSum += monitor(tmp.x, tmp.y, 2);
} else {
tmpSum += monitor(tmp.x, tmp.y, 1);
tmpSum += monitor(tmp.x, tmp.y, 3);
}
continue;
case 3:
tmpSum += monitor(tmp.x, tmp.y, tmpDir);
tmpSum += monitor(tmp.x, tmp.y, (tmpDir+1)%4);
continue;
case 4:
tmpSum += monitor(tmp.x, tmp.y, (tmpDir+1)%4);
tmpSum += monitor(tmp.x, tmp.y, (tmpDir+2)%4);
tmpSum += monitor(tmp.x, tmp.y, (tmpDir+3)%4);
continue;
case 5:
tmpSum += monitor(tmp.x, tmp.y, 0);
tmpSum += monitor(tmp.x, tmp.y, 1);
tmpSum += monitor(tmp.x, tmp.y, 2);
tmpSum += monitor(tmp.x, tmp.y, 3);
continue;
}
}
if (max < tmpSum) max = tmpSum;
}
System.out.println(n*m - max - cctvs.size() - wallsN);
}
private static int monitor(int x, int y, int direction) {
int cnt = 0;
while (true) {
x = x + dx[direction];
y = y + dy[direction];
if (y < 0 || x < 0 || x > n-1 || y > m-1 || board[x][y] == 6) break;
if (board[x][y] != 0 || monitored[x][y]) continue;
monitored[x][y] = true;
cnt++;
}
return cnt;
}
private static void fourJinsu(int[] directions, int caseNum) {
for (int i = 0; i < directions.length; i++) {
directions[i] = caseNum % 4;
caseNum = caseNum / 4;
}
}
}
또 느낀 구현 문제의 특징은 코드가 엄청 지저분해지기 쉽다는 것이었다. 많은 연습이 필요할 것 같다.
monitor 함수는 cctv의 위치와 방향을 인자로 받아 해당 cctv가 cover하는 감시 범위 크기를 반환해주는 함수다. 이것을 각각 경우의 수 별로 모두 더해서, 다른 경우의 수와 계속해서 비교하는 과정을 통해 최댓값을 구할 수 있다.
처음에는 감시하는 방향에 따라 함수를 따로 구현했었는데 dx, dy 배열을 선언해서 dir을 인덱스로 방향을 지정할 수 있도록 해서 코드의 중복을 줄였다. 코드가 간결해졌다.
또, 구현 문제에서는 경우의 수를 구해야하는 상황이 많은데, n진수를 활용해서 경우의 수를 구하는 방법이 있다. 모든 변수들이 독립적인 경우에는, 모든 경우의 수 (이 문제에서는 4^5)에 대해 4진법으로 변환해서, 각 자릿수의 0,1,2,3을 cctv의 방향으로써 사용하면 된다. 써먹을 데가 많은 스킬인 것 같다.
2. 백준 18808 - 스티커 붙이기
1번 문제처럼 board를 첫번째 칸부터 확인해가며 스티커 방향의 모든 경우에 대해서 검사하면 되는 문제였다.
- board 왼쪽 위부터 쭉 검사
- 빈칸 만나면 스티커 크기 (r,c)에 대해서 스티커가 있는 부분이 비어있는지 검사
2-1. 그렇다면, 붙이고 다음 스티커에 대해서 반복
2-2. 그렇지 않다면, 계속 검사 - 끝까지 못찾으면, 스티커 돌린 뒤 처음부터 검사
package simulation;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class BOJ18808 {
static boolean[][] tmpSticker;
static boolean[][] laptop;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
laptop = new boolean[n][m];
int nSticker = Integer.parseInt(st.nextToken());
int cnt = 0;
for (int i = 0; i < nSticker; i++) {
//스티커 초기 설정
st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
tmpSticker = new boolean[x][y];
for (int j = 0; j < x; j++) {
st = new StringTokenizer(br.readLine());
for (int k = 0; k < y; k++) {
if (st.nextToken().equals("1")) tmpSticker[j][k] = true;
}
}
//스티커 붙일 수 있는 지 검사 후 붙이기
a : for (int l = 0; l < 4; l++){
for (int j = 0; j < n; j++) {
for (int k = 0; k < m; k++) {
if (isAttachable(j, k)) {
cnt += attach(j, k);
break a;
}
}
}
rotate(x, y);
int tmp = x;
x = y;
y = tmp;
}
}
System.out.println(cnt);
}
private static boolean isAttachable(int row, int col) {
for (int i = 0; i < tmpSticker.length; i++) {
for (int j = 0; j < tmpSticker[0].length; j++) {
if (row+i >= laptop.length || col+j >= laptop[0].length) return false;
if (laptop[row+i][col+j] && tmpSticker[i][j]) return false;
}
}
return true;
}
private static int attach(int row, int col) {
int answer = 0;
for (int i = 0; i < tmpSticker.length; i++) {
for (int j = 0; j < tmpSticker[0].length; j++) {
if (tmpSticker[i][j]) {
laptop[row+i][col+j] = true;
answer++;
}
}
}
return answer;
}
private static void rotate(int x, int y) {
boolean[][] newThang = new boolean[y][x];
int cnt = 0;
for (int i = 0; i < y; i++) { //열에 대한 검사
for (int j = x-1; j >= 0; j--) { //행에 대한 검사
newThang[cnt / x][cnt % x] = tmpSticker[j][i];
cnt++;
}
}
tmpSticker = newThang;
int tmp = x;
x = y;
y = tmp;
}
private static void showBoard() {
for (int i = 0; i < tmpSticker.length; i++) {
System.out.println(Arrays.toString(tmpSticker[i]));
}
}
}
isAttachable 함수는 이미 붙어있는 스티커와 현재 스티커를 확인해가며 스티커를 해당 위치에 붙일 수 있는 지 확인하고, attach함수는 laptop에 스티커를 추가하고, 붙인 스티커의 크기를 반환한다.
3. 백준 12100 - 2048 (Easy)
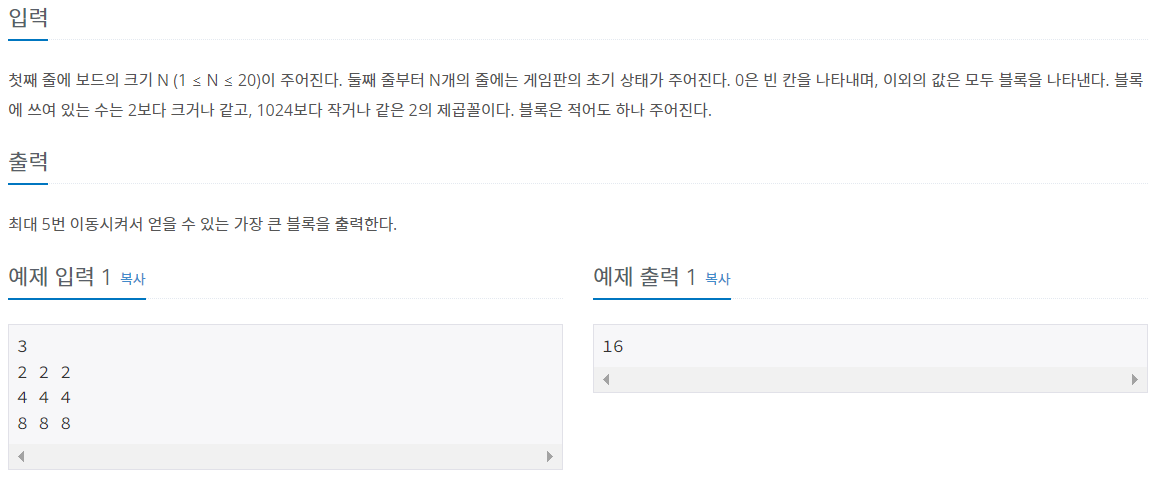
앞의 두 문제보다 구현의 아이디어를 생각해내기 어려운 문제였다. 앞의 문제들처럼 모든 이동의 경우에 수에 대해 검사하는 것은 똑같았다. 처음 생각했던 방법은 각 이동에 대해서 행/열 별로 검사해가면서 인덱스를 활용해 인접한 숫자들이 같은 수가 있는 지를 확인하고 이동시키는 방법이었다.
static void up(int[][] tmpBoard) {
boolean prevChecked = false;
for (int j = 0; j < n; j++) { //col
int prev = 0; //이전 숫자의 idx 저장
for (int i = 1; i < n; i++) { // row
if (tmpBoard[i][j] == 0){
prevChecked = false;
continue;
}
if (tmpBoard[i][j] == tmpBoard[prev][j] && !prevChecked) {
prevChecked = true;
tmpBoard[prev][j] = 2*tmpBoard[prev][j];
tmpBoard[i][j] = 0;
}
//다른 숫자를 만났을 때
else {
prevChecked = false;
if (tmpBoard[prev][j] == 0) {
int tmp = tmpBoard[i][j];
tmpBoard[i][j] = 0;
tmpBoard[prev][j] = tmp;
} else{
int tmp = tmpBoard[i][j];
tmpBoard[i][j] = 0;
tmpBoard[prev+1][j] = tmp;
prev = prev+1;
}
}
}
}
}위로 이동시키는 함수를 이렇게 구현했다. 이전에 숫자가 있는 인덱스를 저장해서 현재 검사하는 숫자와 비교하는 방식이었는데, 이 방법은 한 번의 이동에서 합쳐진 숫자는 다시 합쳐질 수 없다는 조건이나, 행/열의 마지막이 0인 경우 등 예외적인 경우를 처리하기가 너무 어려웠다.
그래서 그 다음으로 내가 생각한 방법은 deque를 이용해서 그 줄의 요소들을 저장한 뒤에 그 줄에 순서대로 다시 저장하는 것이었다. 스택을 활용한 괄호 문제 풀이처럼 말이다.
package simulation;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.StringTokenizer;
public class BOJ12100_2 {
static int[][] board;
static int[][] tmpBoard;
static int n;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
board = new int[n][n];
for (int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for (int j = 0; j < n; j++) {
board[i][j] = Integer.parseInt(st.nextToken());
}
}
int[] direction = new int[5];
int answer = 0;
for (int i = 0; i < 1024; i++) {
tmpBoard = new int[n][n];
for (int j = 0; j < n; j++) {
tmpBoard[j] = Arrays.copyOf(board[j], n);
}
fourJinsu(direction, i);
// System.out.println(Arrays.toString(direction));
for (int x : direction) {
switch (x) {
case 0 : up2(tmpBoard);
break;
case 1 : right2(tmpBoard);
break;
case 2 : down2(tmpBoard);
break;
case 3 : left2(tmpBoard); break;
}
}
answer = maxNum(tmpBoard) > answer ? maxNum(tmpBoard) : answer;
}
System.out.println(answer);
}
private static void showBoard() {
for (int i = 0; i < n; i++) {
System.out.println(Arrays.toString(tmpBoard[i]));
}
}
private static void fourJinsu(int[] direction, int n) {
for (int i = 0; i < 5; i++) {
direction[i] = n % 4;
n = n / 4;
}
}
private static int maxNum(int[][] tmpBoard) {
int answer = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (tmpBoard[i][j] > answer) answer = tmpBoard[i][j];
}
}
return answer;
}
//왼쪽으로 쌔리는경우
static void left2(int[][] tmpBoard) {
for (int i = 0; i < n; i++) {
LinkedList<Integer> deque = new LinkedList<>();
for (int j = 0; j < n; j++) {
if (tmpBoard[i][j] == 0) continue;
if (!deque.isEmpty() && deque.peekLast() == tmpBoard[i][j]) {
deque.offer(deque.pollLast()*2);
deque.offer(-1);
} else {
deque.offer(tmpBoard[i][j]);
}
tmpBoard[i][j] = 0;
}
int cnt = 0;
while (!deque.isEmpty()) {
int tmp = deque.poll();
if (tmp != -1) tmpBoard[i][cnt++] = tmp;
}
}
}
static void right2(int[][] tmpBoard) {
LinkedList<Integer> deque = new LinkedList<>();
for (int i = 0; i < n; i++) {
deque.clear();
for (int j = n-1; j >= 0; j--) {
if (tmpBoard[i][j] == 0) continue;
if (!deque.isEmpty() && deque.peekLast() == tmpBoard[i][j]) {
deque.offer(deque.pollLast()*2);
deque.offer(-1);
} else {
deque.offer(tmpBoard[i][j]);
}
tmpBoard[i][j] = 0;
}
int cnt = n-1;
while (!deque.isEmpty()) {
int tmp = deque.poll();
if (tmp != -1) tmpBoard[i][cnt--] = tmp;
}
}
}
static void up2(int[][] tmpBoard) {
LinkedList<Integer> deque = new LinkedList<>();
for (int j = 0; j < n; j++) {
for (int i = 0; i < n; i++) {
if (tmpBoard[i][j] == 0) continue;
if (!deque.isEmpty() && deque.peekLast() == tmpBoard[i][j]) {
deque.offer(deque.pollLast()*2);
deque.offer(-1);
} else {
deque.offer(tmpBoard[i][j]);
}
tmpBoard[i][j] = 0;
}
int cnt = 0;
while (!deque.isEmpty()) {
int tmp = deque.poll();
if (tmp != -1) tmpBoard[cnt++][j] = tmp;
}
}
}
static void down2(int[][] tmpBoard) {
LinkedList<Integer> deque = new LinkedList<>();
for (int j = 0; j < n; j++) {
for (int i = n-1; i >= 0; i--) {
if (tmpBoard[i][j] == 0) continue;
if (!deque.isEmpty() && deque.peekLast() == tmpBoard[i][j]) {
deque.offer(deque.pollLast()*2);
deque.offer(-1);
} else {
deque.offer(tmpBoard[i][j]);
}
tmpBoard[i][j] = 0;
}
int cnt = n-1;
while (!deque.isEmpty()) {
int tmp = deque.poll();
if (tmp != -1) tmpBoard[cnt--][j] = tmp;
}
}
}
}
이동시키는 함수들을 보면, deque에 스택처럼 저장해가며 같은 숫자가 나오면, 추가하지 않고 두 배의 값으로 저장해준 뒤에, -1을 추가해서 두 번 연속으로 합쳐지지 않도록 했다. 그리고 나서 덱에 있는 -1을 제외한 요소들을 이동하려는 방향에서부터 순서대로 저장해줬다.
그 외의 코드는 어려운 부분은 없었다.
4. 백준 15686 - 치킨 배달
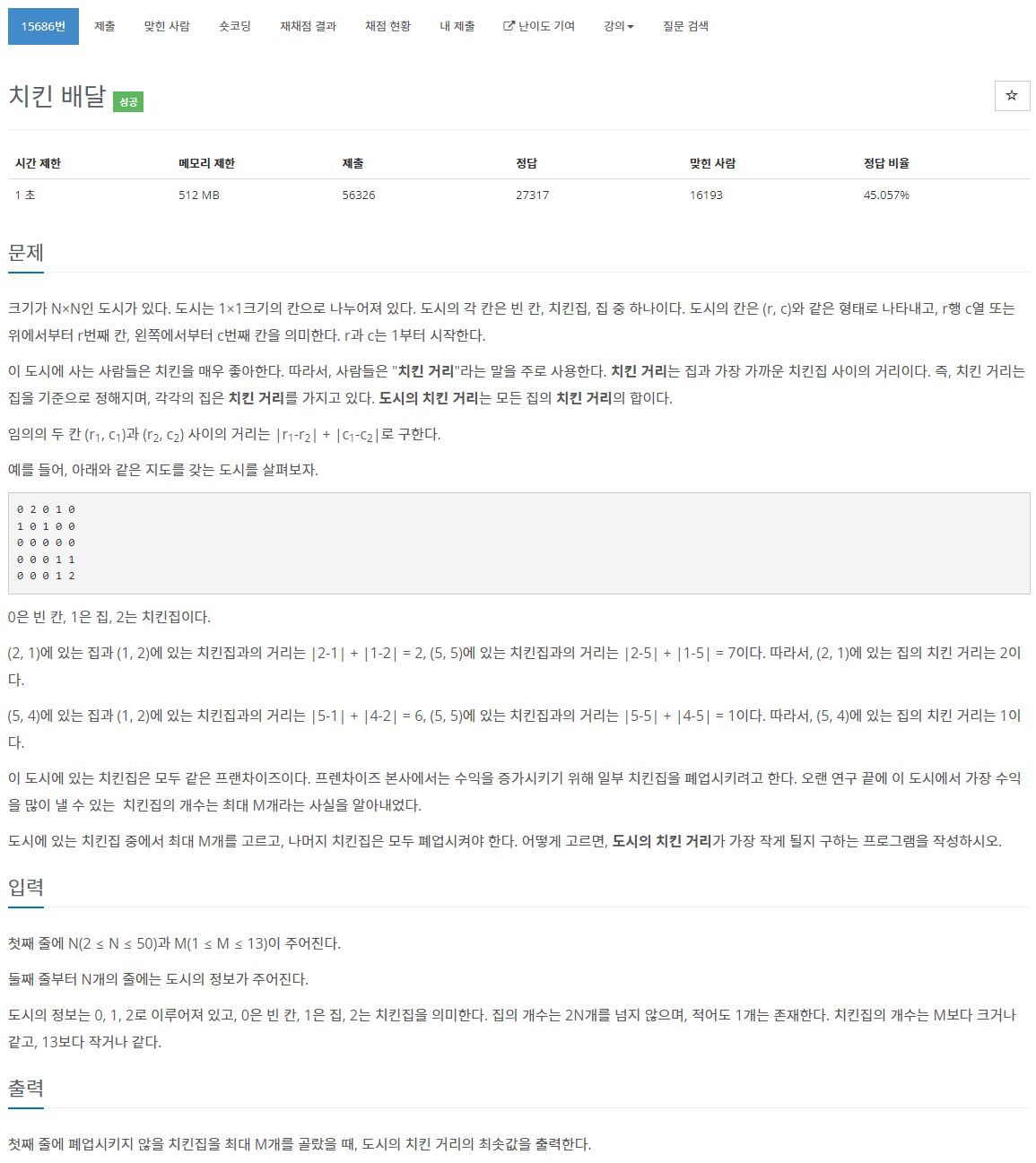모든 치킨집의 개수 중 M개를 선택하는 경우 (cCm)에 대해서, 각각의 집의 치킨거리를 모두 더해서 도시의 치킨 거리를 구하고, 이 중 최솟값을 구하면 되겠다.
package simulation;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
class Coordinate {
int x;
int y;
public Coordinate(int x, int y) {
this.x = x;
this.y = y;
}
}
public class BOJ15686 {
static List<Coordinate> houses = new ArrayList<>();
static List<Coordinate> chickens = new ArrayList<>();
static boolean[] survived;
static int[][] board;
static int n;
static int m;
static int answer = Integer.MAX_VALUE;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
board = new int[n][n];
for (int i = 0; i < n; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < n; j++) {
int tmp = Integer.parseInt(st.nextToken());
if (tmp == 1) houses.add(new Coordinate(i, j));
else if (tmp == 2) chickens.add(new Coordinate(i, j));
board[i][j] = tmp;
}
}
survived = new boolean[chickens.size()];
chickenComb(0,0);
System.out.println(answer);
}
private static void chickenComb(int depth, int start) {
if (depth == m) {
int tmpMin = chickenDistance();
answer = answer < tmpMin ? answer : tmpMin;
// System.out.println(Arrays.toString(survived));
}
for (int i = start; i < survived.length; i++) {
survived[i] = true;
chickenComb(depth+1, i+1);
survived[i] = false;
}
}
private static int chickenDistance() {
int distance = 0;
for (Coordinate house : houses) {
int minDist = Integer.MAX_VALUE;
for (int i = 0; i < chickens.size(); i++) {
if (!survived[i]) continue;
int tmpDist = Math.abs(house.x - chickens.get(i).x) + Math.abs(house.y - chickens.get(i).y);
minDist = minDist < tmpDist ? minDist : tmpDist;
}
distance += minDist;
}
return distance;
}
}
전체 치킨집의 개수에서 m개를 뽑는 것은 위 문제들처럼 독립적인 경우가 아니기 때문에 백트래킹을 이용했다. chickenComb 함수로 모든 경우의 수를 구하고, 바로 치킨거리를 구하는 chickenDistance()를 호출하도록 했다.
chickenDistance()함수는 해당하는 경우에서, 각 집에서 가장 가까운 치킨집까지의 거리를 모두 더해 그 경우의 전체 치킨거리의 합을 반환한다. 그러면 chickenComb()에서 static 변수인 answer에 최솟값을 자동적으로 구할 수 있게 된다.
끝
이렇게 해서 시뮬레이션 연습 문제들을 네 개 풀어봤다. 시뮬레이션 문제를 처음 접하면서 내가 느낀 점은 다음과 같다.
- 문제의 요구사항을 정확하게 이해하는 것이 가장 중요하다. 시뮬레이션 문제는 우선 지문의 길이 자체가 길기 마련이다. 요구하는 사항이 다른 문제에 비해 복잡하기 때문이다. 이것을 완전히 이해하고 정리해야 구현이 훨씬 쉬워진다. 나는 그래서 모든 문제를 풀 때 노트에 직접 시각적으로 표현해서 시뮬레이션을 돌려봤다.
- 예외 케이스를 꼼꼼히 보야아한다. 1번과 이어지는 부분인데, 문제에서 요구하는 것 자체가 조금 복잡하기 때문에, 내가 구현한 해결책이 요구하는 사항에 완전히 부합하는지 꼼꼼히 확인해야한다.
- 구현이 너무 재밌당. 오늘 해결한 문제들이 삼성 SW역량 코딩테스트? 의 문제라는 것을 염두에 두고 풀어서 그런지 더 뿌듯한 것도 있었지만, 무엇보다도 구현 문제는 레고를 조립해서 무언가를 만들어내는 듯한 느낌이 있어 더 재밌었다.
시뮬레이션 문제들은 특히나 많이 풀어봄으로써 구현력을 기를 수 있을 것 같다. 다음 포스팅에서는 시뮬레이션 문제들을 몇 개 더 풀어볼 것이다.
연습 문제 출처 : encrypted-def github
컴퓨터 사이언스, 알고리즘, 모든 애플리케이션에 관심이 있습니다.