[프로그래머스] 소수 찾기 (에라토스테네스의 체)

프로그래머스의 소수 찾기 문제를 재귀로 풀었더니 암만 수정해도 시간 초과가 떴다. 에라토스테네스의 체를 활용해보라는 이야기가 있어서 사용해보았다.

에라토스테네스의 체

에라토스테네스의 체는 소수를 찾는 가장 빠르고 쉬운 방법이다.

1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. (사진은 1부터 120까지)

2. 2는 소수이므로 오른쪽에 2를 쓴다. 자기 자신을 제외한 2의 배수를 모두 지운다.

3. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. 자기 자신을 제외한 3의 배수를 모두 지운다.

4. 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. 자기 자신을 제외한 5의 배수를 모두 지운다.

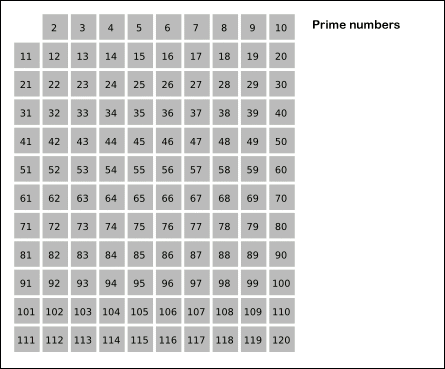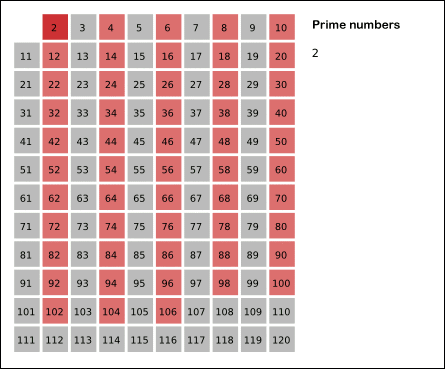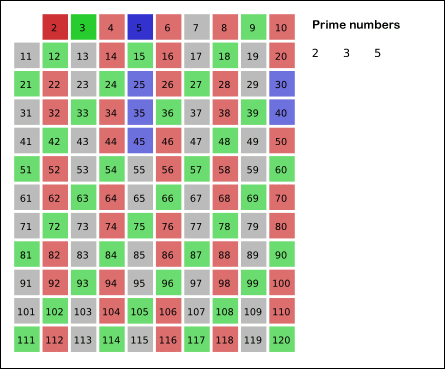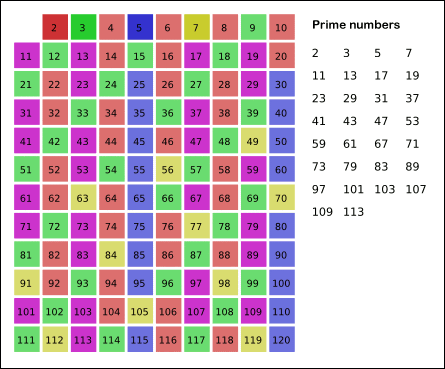
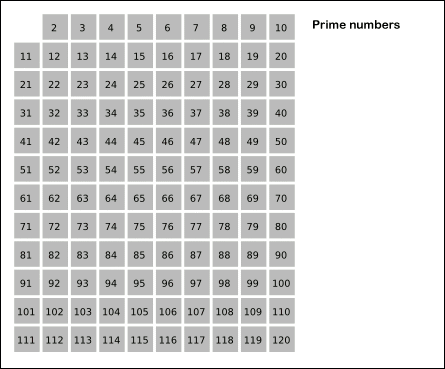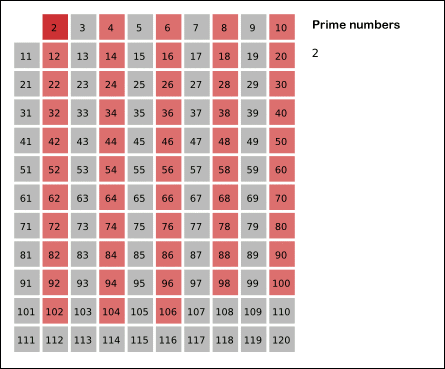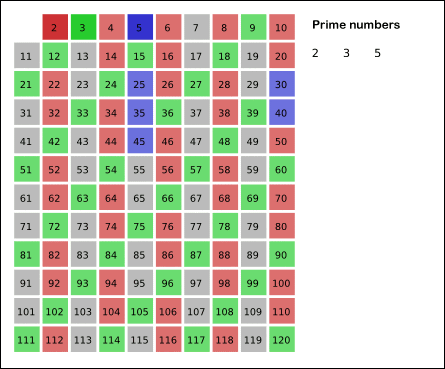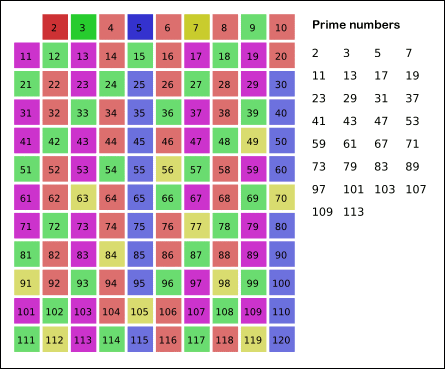
5. 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. 자기 자신을 제외한 7의 배수를 모두 지운다.

6. 위의 과정을 반복하면 구하는 구간의 소수를 구할 수 있다.

그림의 경우, 11의 제곱 < 120 이므로 11보다 작은 수의 배수들만 지워도 충분하다.

즉, 2부터 배수를 지운 후 남은 수 중 가장 작은 소수를 찾아 배수를 지우는 작업을 반복하는 방식이다.

"√n까지만 검사해도 된다” 라는 뜻은 배수를 지울 필요가 없다는 게 아니라, 더 이상 새로운 배수를 지울 필요가 없다는 뜻!
즉, 이미 앞서 검사를 하면서 배수가 다 지워졌기 때문이다.

풀이 코드

에라토스테네스의 체를 활용해서 문제를 풀면 다음과 같다.

function solution(n) {
    let primes = new Array(n + 1).fill(true); // 전부 소수로 가정
    primes[0] = primes[1] = false; // 0과 1은 소수가 아님

    for (let i = 2; i * i <= n; i++) {  
        if (primes[i]) {  // 만약 소수일 경우
            for (let j = i * i; j <= n; j += i) {  
              	// i * i부터 i의 배수는 소수가 아님
                primes[j] = false;
            }
        }
    }
    // return 소수의 개수
    return primes.filter((prime) => prime === true).length;
}

코드 설명

    let primes = new Array(n + 1).fill(true); 
    primes[0] = primes[1] = false; 

• index가 0부터 시작하기 때문에 편의를 위해 n + 1(인덱스 기준: 0 ~ n)까지 배열을 만든다.
• 이때 배열에 있는 숫자는 모두 소수라고 가정한다.
• 0과 1은 소수가 아니기 때문에 false를 할당한다.

for (let i = 2; i * i <= n; i++) {  
    if (primes[i]) { 
        for (let j = i * i; j <= n; j += i) {  
           primes[j] = false;
        }
    }
}

• 2부터 i * i가 n보다 작을 때까지 for문을 반복한다
  - i가 √n까지만 검사를 하면 되기 때문(남은 배수는 앞에서 이미 지워짐)
• 만약 소수일 경우, i * i부터 i의 배수들을 지워준다.

⚠️ i * i부터 배수를 지우는 이유 ⚠️
예를 들어, i = 3이면

• 3 * 2 = 6
• 3 * 3 = 9
• 3 * 4 = 12
  ➡️ 이미 앞에서 2를 지웠기 때문에 불필요하게 또 제거를 할 필요가 없다!

return primes.filter((prime) => prime === true).length;

• primes 배열에서 true인 것이 소수이기 때문에 filter 메서드를 사용해서 걸러준 후 개수를 반환해준다.

이런식으로 구하면 재귀보다 빠르게 소수를 찾아낼 수 있다.

출처

에라토스테네스의 체 (위키백과)