
0. 문제 설명
김 프로는 수영장을 이용한다.
김 프로는 지출이 너무 많아 내년 1년 동안 각 달의 이용 계획을 수립하고 가장 적은 비용으로 수영장을 이용할 수 있는 방법을 찾고 있다.
수영장에서 판매하고 있는 이용권은 아래와 같이 4 종류이다.
① 1일 이용권 : 1일 이용이 가능하다.
② 1달 이용권 : 1달 동안 이용이 가능하다. 1달 이용권은 매달 1일부터 시작한다.
③ 3달 이용권 : 연속된 3달 동안 이용이 가능하다. 3달 이용권은 매달 1일부터 시작한다.
(11월, 12월에도 3달 이용권을 사용할 수 있다 / 다음 해의 이용권만을 구매할 수 있기 때문에 3달 이용권은 11월, 12월, 1윌 이나 12월, 1월, 2월 동안 사용하도록 구매할 수는 없다.)
④ 1년 이용권 : 1년 동안 이용이 가능하다. 1년 이용권은 매년 1월 1일부터 시작한다.
각 달의 이용 계획은 [Table 1]의 형태로 수립된다.

[Table 1]
이용 계획에 나타나는 숫자는 해당 달에 수영장을 이용할 날의 수를 의미한다.
각 이용권의 요금과 각 달의 이용 계획이 입력으로 주어질 때,
가장 적은 비용으로 수영장을 이용할 수 있는 방법을 찾고 그 비용을 정답으로 출력하는 프로그램을 작성하라.
[예시]
수영장에서 판매하는 1일 이용권, 1달 이용권, 3달 이용권, 1년 이용권의 요금은 각각 10원, 40원, 100원, 300원이다.
이 때 수영장을 이용할 수 있는 방법은 [Table 2]와 같이 다양한 경우를 생각할 수 있다.
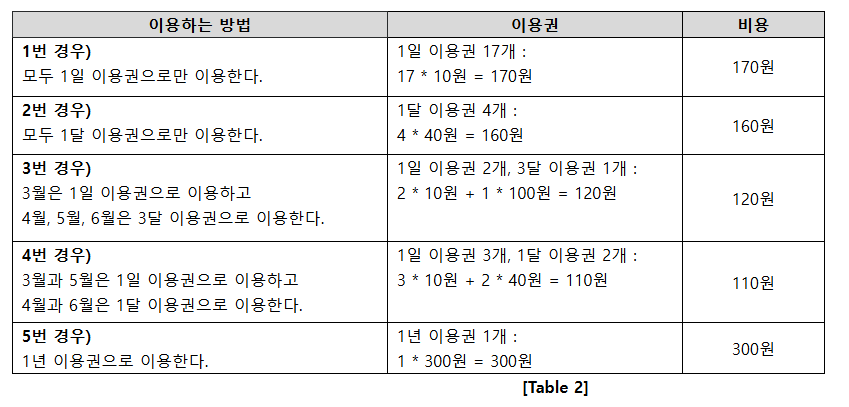
[Table 2]
다른 경우도 가능하지만, 가장 적은 비용으로 수영장을 이용한 경우는 4번 경우이다.
따라서, 정답은 110이 된다.
[제약 사항]
-
시간 제한 : 최대 50개 테스트 케이스를 모두 통과하는 데 C/C++/Java 모두 3초
-
모든 종류의 이용권 요금은 10 이상 3,000 이하의 정수이다.
-
각 달의 이용 계획은 각 달의 마지막 일자보다 크지 않다.
[입력]
입력의 맨 첫 줄에는 총 테스트 케이스의 개수 T가 주어지고, 그 다음 줄부터 T개의 테스트 케이스가 주어진다.
각 테스트 케이스의 첫 번째 줄에는 1일 이용권의 요금, 1달 이용권의 요금, 3달 이용권의 요금, 1년 이용권의 요금이 순서대로 한 칸씩 띄고 주어진다.
그 다음 줄에는 1월부터 12월까지의 이용 계획이 주어진다.
[출력]
테스트 케이스 개수만큼 T개의 줄에 각각의 테스트 케이스에 대한 답을 출력한다.
각 줄은 "#t"로 시작하고 공백을 하나 둔 다음 정답을 출력한다. (t는 1부터 시작하는 테스트 케이스의 번호이다)
출력해야 할 정답은 이용 계획대로 수영장을 이용하는 경우 중 가장 적게 지출하는 비용이다.
1. 문제 해석
먼저 문제를 정확히 정의해야 한다. 우리에게 주어진 정보는 다음과 같다.
- 가격 정보: 1일권, 1달권, 3달권, 1년권의 가격.
- 이용 계획: 1월부터 12월까지 월별 수영장 이용 예정일 수.
우리의 목표는 이 정보들을 조합하여 1년간의 총비용을 최소화하는 것이다.
단순히 보면 매달 가장 싼 선택을 하면 될 것 같지만, '3달 이용권'의 존재가 문제를 복잡하게 만든다. 예를 들어, 3월의 요금을 결정할 때, 1월과 2월에 어떤 선택을 했는지가 3월의 결정에 영향을 미친다. 1, 2, 3월을 각각 1달권으로 끊는 것보다 1-3월을 묶어 3달권 하나로 처리하는 것이 더 저렴할 수 있기 때문이다. 이처럼 특정 시점의 최적 결정이 이전 시점들의 최적 결정에 의존하는 구조를 최적 부분 구조라 부른다.
또한, 특정 월까지의 최소 비용을 계산하는 과정에서 그 이전 달들의 최소 비용 계산이 반복적으로 필요하게 되는데, 이를 중복되는 부분 문제라 한다. 이 두 가지 특성은 DP를 적용할 수 있는 강력한 신호다.
2. DP 설계 단계 설명
DP의 핵심은 큰 문제를 작은 부분 문제로 나누어 해결하고, 그 해결책을 저장해두었다가 필요할 때 재사용하는 것이다. '수영장' 문제에 이 전략을 적용해 보자.
1단계: DP 상태(State) 정의
가장 중요한 과정이다. 우리는 무엇을 계산하고 기록할 것인가? DP 배열의 각 요소가 의미하는 바를 명확히 해야 한다.
dp[i]=i월까지의 모든 이용 계획을 만족시키는 데 필요한 누적 최소 비용
이렇게 상태를 정의하면, 우리의 최종 목표는 12월까지의 모든 계획을 만족시키는 최소 비용, 즉 dp[12]를 계산하는 것이 된다.
2단계: 베이스 케이스 설정
모든 재귀적 계산은 시작점이 필요하다. dp 배열의 계산을 시작하기 위한 기준점은 무엇일까?
dp[0] = 0
이는 '0월까지', 즉 아무것도 시작하기 전의 비용은 0이라는 의미다. 이 값은 1월(dp[1]), 2월(dp[2]), 3월(dp[3])의 비용을 계산하는 최초의 기반이 된다.
3단계: 점화식 설계
dp[i]는 그 이전의 dp 값들을 이용해 어떻게 계산될 수 있는가? i월까지의 최소 비용을 확정하기 위해, i월을 처리하는 가능한 모든 방법을 고려하고 그중 최솟값을 찾아야 한다.
i월의 이용 계획을 처리하는 방법은 크게 두 가지 시나리오로 나눌 수 있다.
시나리오 A: i월을 1일권 또는 1달권으로 해결하는 경우
이 시나리오는 i월을 독립적인 한 달로 취급한다.
i월 자체의 최소 비용은(i월 이용일 수 * 1일권 가격)과1달권 가격중 더 저렴한 값이다.- 이 방법을 선택했을 때
i월까지의 총 누적 비용은,(i-1)월까지의 누적 최소 비용)에(i월 자체의 최소 비용)을 더한 값이 된다. - 식:
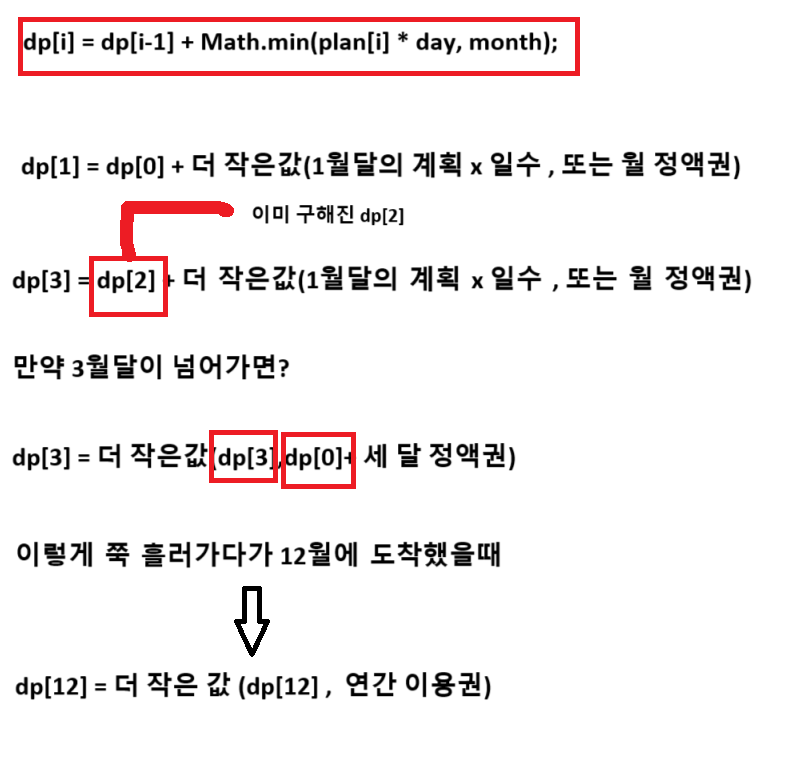
dp[i-1] + Math.min(plan[i] * day, month)
시나리오 B: i월을 3달 이용권의 마지막 달로서 해결하는 경우
이 시나리오는 i-2, i-1, i월을 하나의 묶음으로 취급한다. (단, i가 3 이상일 때만 가능)
- 이 3개월 묶음의 비용은
3달권 가격이다. - 이 방법을 선택했을 때
i월까지의 총 누적 비용은,(i-3)월까지의 누적 최소 비용)에(3달권 가격)을 더한 값이 된다. 3달권을 시작하기 직전인i-3월까지의 최적해가 필요하기 때문이다. - 식:
dp[i-3] + threeMonth
dp[i]는 이 두 시나리오 중 더 저렴한 쪽이어야 한다. 따라서, 최종 점화식은 다음과 같이 완성된다.
- 일단 시나리오 A를
dp[i]의 후보값으로 설정한다.
dp[i] = dp[i-1] + Math.min(plan[i] * day, month) - 만약
i가 3 이상이라면, 시나리오 B와 비교하여 더 작은 값으로 갱신한다.
dp[i] = Math.min(dp[i], dp[i-3] + threeMonth)
4단계: 최종 해 도출
위 점화식을 통해 dp[1]부터 dp[12]까지 순차적으로 계산하면, dp[12]에는 1일권, 1달권, 3달권을 조합했을 때의 연간 최소 비용이 저장된다.
하지만 아직 마지막 카드가 남아있다. 바로 1년 이용권이다. 1년 이용권은 월별 계산 과정에 포함되지 않는, 전체 계획을 한 번에 해결하는 독립적인 옵션이다. 따라서 DP로 계산한 최적해 dp[12]와 1년권 가격을 최종적으로 비교해야 진짜 전역 최적해(Global Optimum)를 찾을 수 있다.
최종 정답 =
Math.min(dp[12], year)
3. 코드 구현 심층 분석
이제 위 설계에 기반한 Java 코드를 한 줄 한 줄 면밀히 분석한다.
import java.io.*;
import java.util.*;
public class 수영장 {
public static void main(String[] args) throws IOException {
// 섹션 1: 입력 처리 및 변수 초기화
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int tc = Integer.parseInt(br.readLine()); // 테스트 케이스 수
for (int t = 1; t <= tc; t++) {
StringTokenizer st;
st= new StringTokenizer(br.readLine());
int day = Integer.parseInt(st.nextToken());
int month = Integer.parseInt(st.nextToken());
int threeMonth = Integer.parseInt(st.nextToken());
int year = Integer.parseInt(st.nextToken());
// 월별 계획을 저장할 배열. 1-based indexing을 위해 크기를 13으로 한다.
// plan[i]가 i월의 계획을 의미하도록 하여 코드의 직관성을 높인다.
int[] plan = new int[13];
st = new StringTokenizer(br.readLine());
for (int i = 1; i < plan.length; i++) {
plan[i] = Integer.parseInt(st.nextToken());
}
// 섹션 2: DP 테이블 생성 및 베이스 케이스 설정
int[] dp = new int[13];
dp[0] = 0; // 베이스 케이스: 0월까지의 비용은 0.
// 섹션 3: 점화식을 이용한 DP 테이블 채우기
for (int i = 1; i < dp.length; i++) {
// 3-1. 시나리오 A: i월을 1일권 또는 1달권으로 처리
// (i-1)월까지의 최적 비용(dp[i-1])에 i월 한 달간의 최적 비용을 더한다.
dp[i] = dp[i-1] + Math.min(plan[i] * day, month);
// 3-2. 시나리오 B: i월을 3달 이용권으로 처리하는 것을 고려 (i>=3)
if (i >= 3) {
// 현재까지 계산된 dp[i] 값과,
// (i-3)월까지의 최적 비용(dp[i-3])에 3달권 비용을 더한 값을 비교한다.
// 더 작은 값으로 dp[i]를 갱신하여 최적해를 유지한다.
dp[i] = Math.min(dp[i], dp[i-3] + threeMonth);
}
}
// 섹션 4: 최종 정답 결정
// 1~3달권 조합의 연간 최적해(dp[12])와 1년권이라는 특수 옵션을 비교한다.
int answer = Math.min(dp[12], year);
System.out.println("#" + t + " " + answer);
}
}
}코드 해설
- 섹션 1 (입력 처리): 표준 입력을 받아 각 이용권의 가격과 월별 이용 계획을 변수와 배열에 저장한다. 여기서
plan과dp배열의 크기를 13으로 잡는 것은 일반적인 코딩 테스트 테크닉으로, 인덱스 0을 더미로 남겨두고 인덱스i가 실제i월을 가리키게 함으로써i-1,i-3같은 인덱스 계산 시 혼동을 줄이고 코드를 명확하게 만든다. - 섹션 2 (DP 테이블 초기화):
dp배열을 생성하고dp[0]을 0으로 설정하여 점화식 계산의 시발점을 마련한다. - 섹션 3 (DP 계산 루프): 이 코드의 심장부다.
for루프가 1월부터 12월까지 순차적으로 돌면서dp테이블을 채워나간다. 각i에서,dp[i]는 이전dp값들을 참조하여 계산된다. 이 순차적 접근 방식 덕분에dp[i]를 계산하는 시점에는dp[i-1]과dp[i-3]이 이미 계산 완료된 상태임이 보장된다.- 먼저 **가장 기본적인 선택지(1일권/1달권)**로
dp[i]를 초기화하고, - 그다음 **더 복잡한 선택지(3달권)**가 가능하다면, 그 경우와 비교하여
dp[i]를 더 나은 값으로 갱신하는 구조다. 이는 DP 문제 해결의 전형적인 패턴이다.
- 먼저 **가장 기본적인 선택지(1일권/1달권)**로
- 섹션 4 (최종 정답): 모든 월별 최적화가 끝난 후,
dp[12]에 저장된 값은 부분적인 선택지들(1일, 1달, 3달권)의 조합으로 만들 수 있는 최상의 결과다. 이 결과와 전체를 한 번에 아우르는 절대적 옵션(1년권)을 비교하여 최종 답을 확정한다.
4. 결론
'수영장' 문제는 왜 DP가 강력한 문제 해결 방법인지를 명확히 보여준다. 복잡하게 얽힌 선택의 연쇄를 상태 정의, 점화식 수립이라는 체계적인 프로세스를 통해 명쾌한 코드로 풀어낼 수 있다.
이 문제의 해결 과정을 통해 얻어야 할 핵심은 다음과 같다.
- 문제의 구조 파악: 최적 부분 구조와 중복 부분 문제가 있는지 확인한다.
- 상태의 명확한 정의:
dp[i]가 무엇을 의미하는지 한 문장으로 정의할 수 있어야 한다. - 모든 경우의 수를 포괄하는 점화식:
dp[i]를 계산하기 위해i시점에서 할 수 있는 모든 선택을 고려하고, 이 선택들이 이전 상태(dp[i-k])와 어떻게 연결되는지를 식으로 표현해야 한다.
