[동빈나/파이썬] 다이나믹 프로그래밍 개념 & 기초 문제 풀이

다이나믹 프로그래밍 조건

1. 최적 부분 구조
   큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제 해결
   
   
2. 중복되는 부분 문제
   동일한 작은 문제를 반복적으로 해결

구현방법

일반 재귀 방식 O(2의 n제곱)

• 메모이제이션(탑다운) O(N)
  한 번 계산한 결과를 메모리 공간에 메모
  

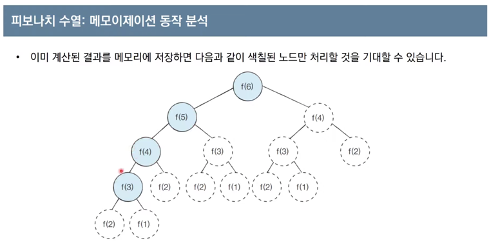
• 바텀업
  

---

기초문제풀이

문제1. 개미 전사

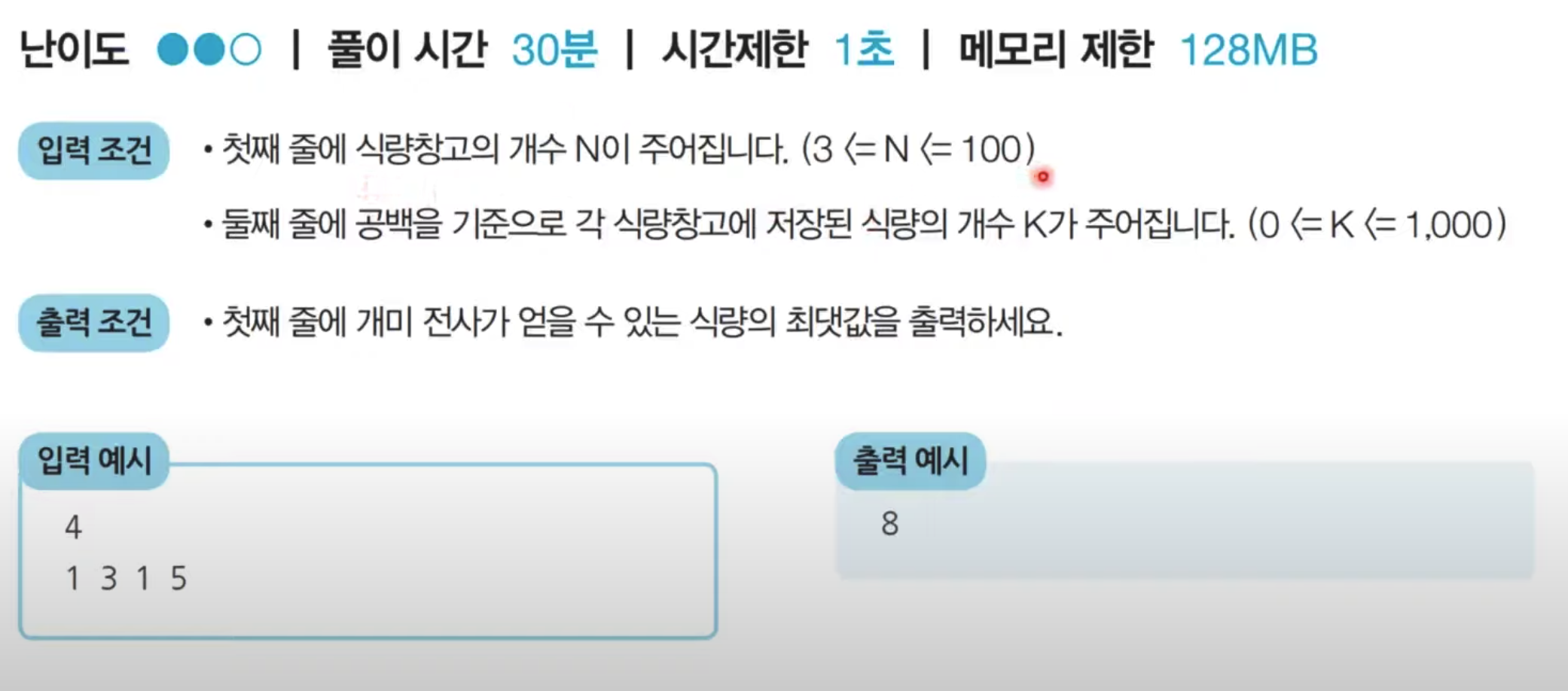
바텀업방식

n=int(input())
array=list(map(int, input().split()))

d=[0]*100

d[0]=array[0]
d[1]=max(array[0],array[1])

for i in range(2, n):
  d[i]=max(d[i-1], d[i-2]+array[i])

print(d[n-1])

문제2. 1로 만들기

바텀업 방식

x=int(input())
d=[0]*30001

for i in range(2, x+1):
  d[i]=d[i-1]+1	#d[i]는 i를 1로 만들기 위한 연산 횟수
  if i%2==0:
    d[i]=min(d[i], d[i//2]+1)
  if i%3==0:
    d[i]=min(d[i], d[i//3]+1)
  if i%5==0:
    d[i]=min(d[i], d[i//5]+1)

print(d[x])

문제3. 효율적인 화폐 구성

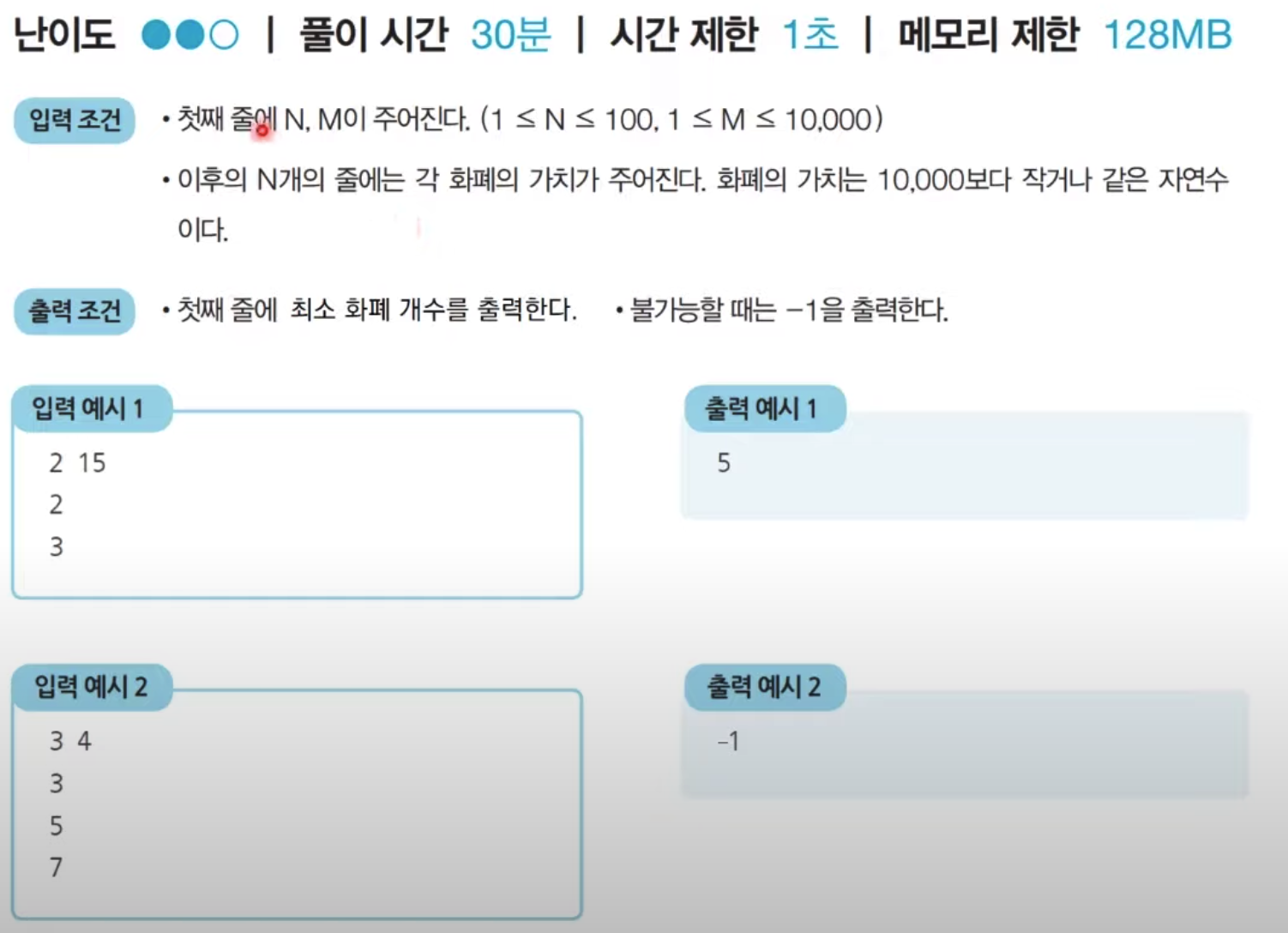
n,m=map(int,input().split())
array=[]
for i in range(n):
  array.append(int(input()))

d=[10001]*(m+1)

d[0]=0 #d[i]는 금액 i를 만들 수 있는 최소 화폐 개수
for i in range(n):
  for j in range(array[i], m+1):
    if d[j-array[i]] != 10001:
      d[j]=min(d[j], d[j-array[i]]+1)

if d[m]==10001:
  print(-1)
else:
  print(d[m])

ex)
[0, 1001, 1, 1001, 2, 1001, 3, 1001, 4, 1001, 5, 1001, 6, 1001, 7, 1001]

[0, 1001, 1, 1, 2, 1001, 3, 1001, 4, 1001, 5, 1001, 6, 1001, 7, 1001]

문제4. 금광

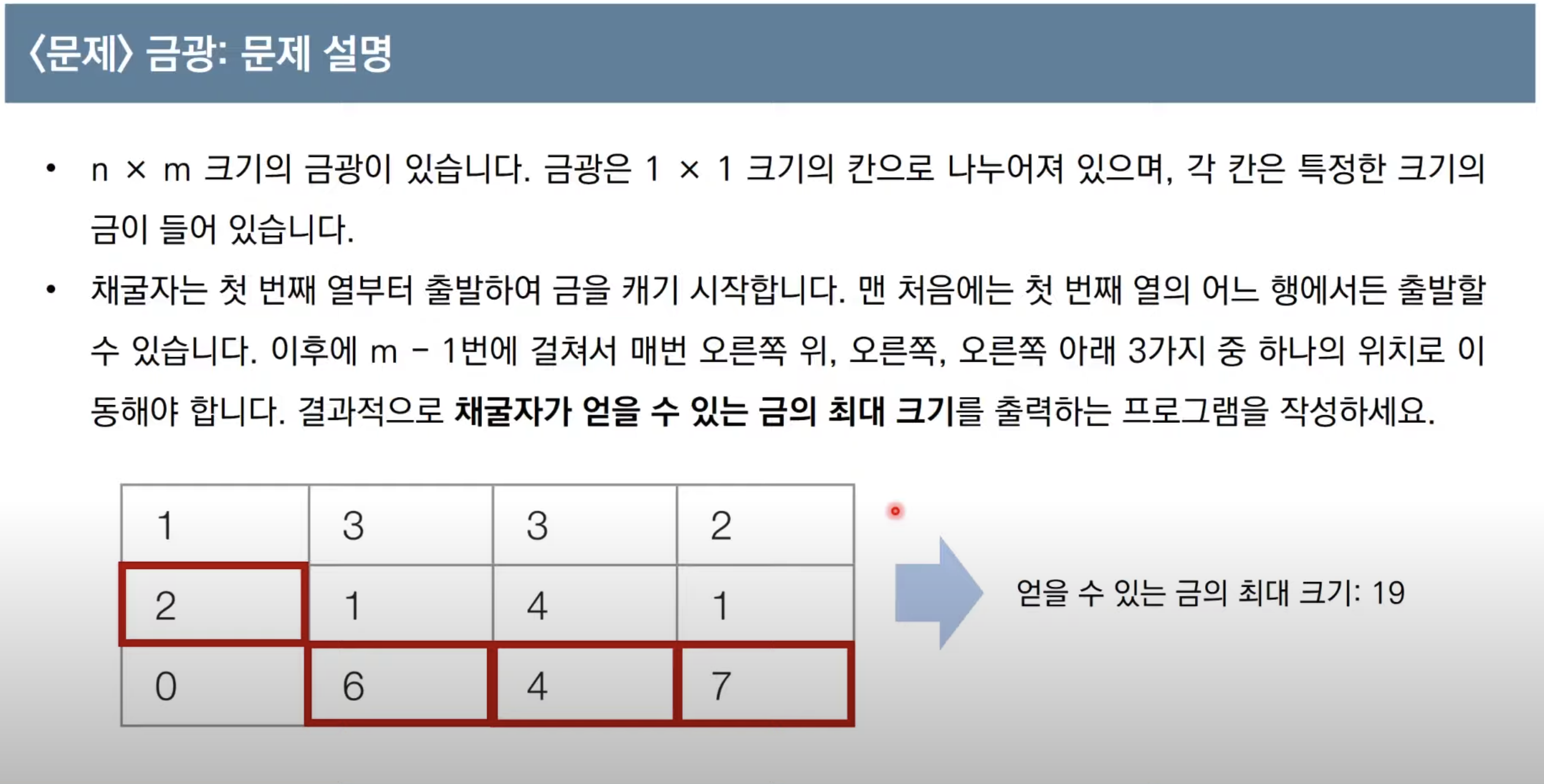
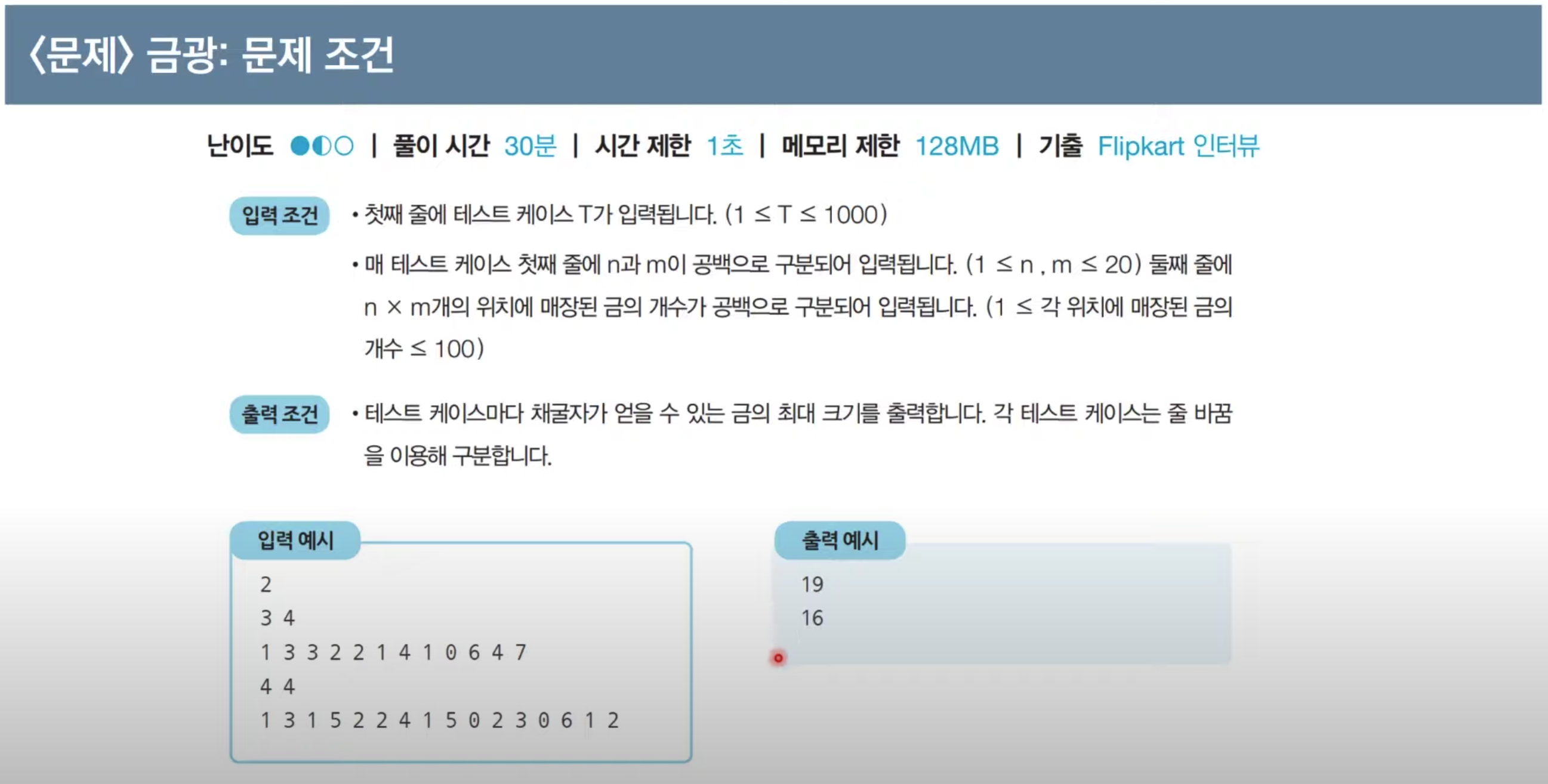
for tc in range(int(input())):
  n,m=map(int, input().split())
  array=list(map(int, input().split()))

  dp=[]
  index=0
  for i in range(n):
    dp.append(array[index:index+m])
    index+=m
    print(dp)

  for j in range(1,m):
    for i in range(n):
      #왼쪽위에서 오는경우
      if i==0:
        left_up=0
      else:
        left_up=dp[i-1][j-1]
      #왼쪽아래
      if i==n-1:
        left_down=0
      else:
        left_down=dp[i+1][j-1]
      #왼쪽
      left=dp[i][j-1]
      dp[i][j]=dp[i][j]+max(left_up,left_down,left)
  result=0
  print(dp)
  for i in range(n):
    result=max(result,dp[i][m-1])
  print(result)

ex)
1
3 4
1 3 3 2 2 1 4 1 0 6 4 7
[[1, 3, 3, 2]]
[[1, 3, 3, 2], [2, 1, 4, 1]]
[[1, 3, 3, 2], [2, 1, 4, 1], [0, 6, 4, 7]]
[[1, 5, 8, 14], [2, 3, 12, 13], [0, 8, 12, 19]]

문제5. 병사 배치하기

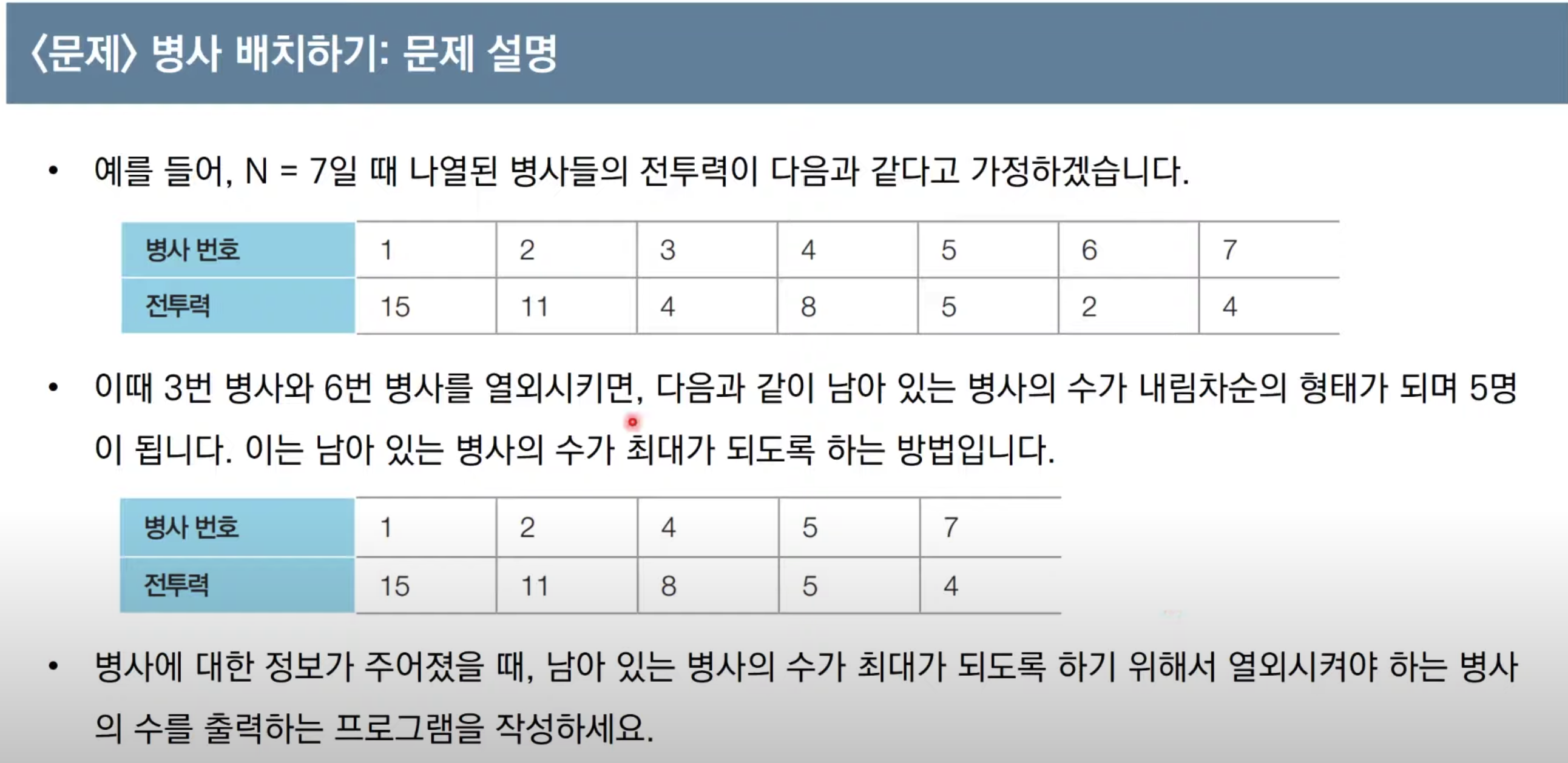
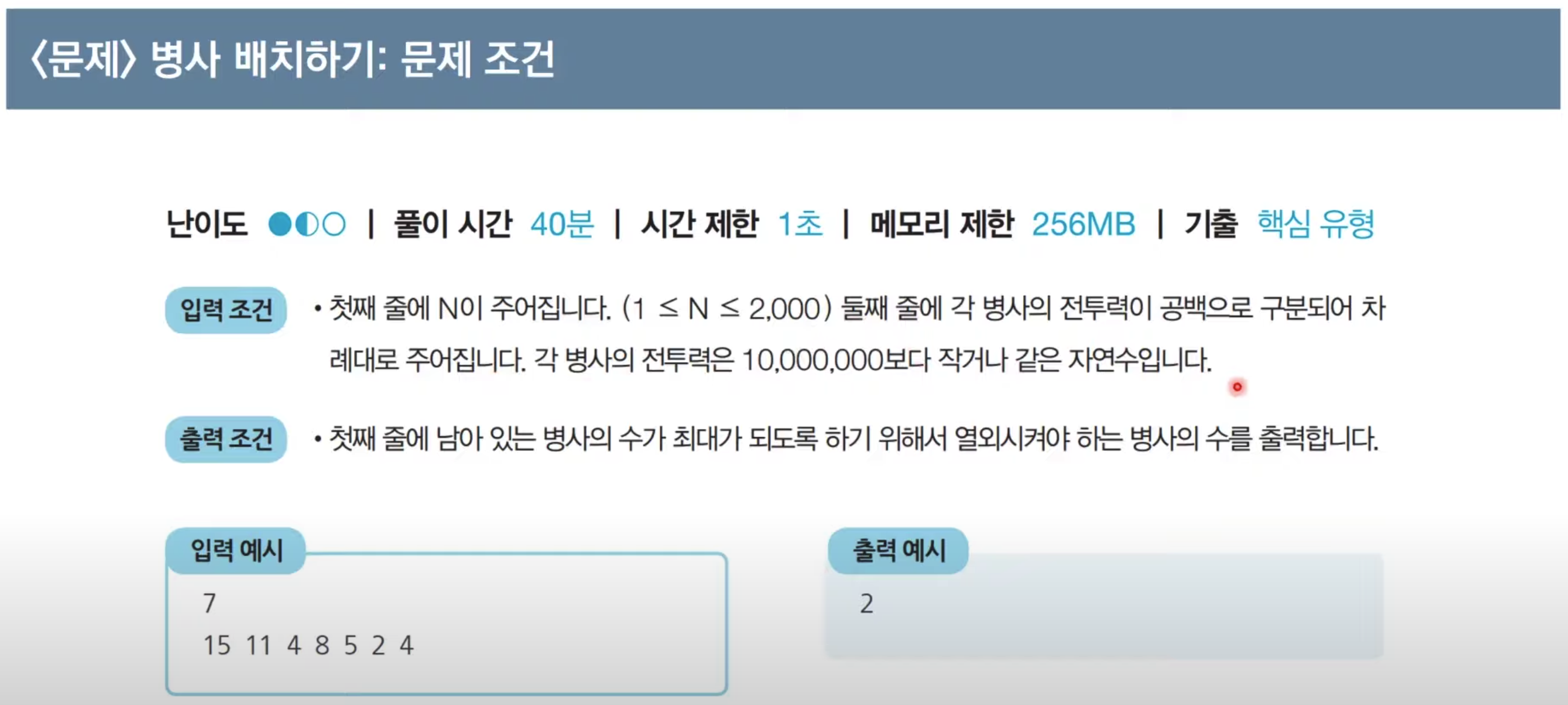
기본 아이디어: 가장 긴 증가하는 부분 수열(LIS)
ex) array={4,2,5,8,4,11,15} -> {4,5,8,11,15}

n=int(input())
array=list(map(int, input().split()))
#순서를 뒤집어 LIS로 전환
array.reverse()

dp=[1]*n

for i in range(1,n):
  for j in range(i):
    if array[j]<array[i]:
      dp[i]=max(dp[i],dp[j]+1)

print(n-max(dp))