[백준/파이썬] 1520 내리막길

https://www.acmicpc.net/problem/1520

---

알고리즘 분류

• DFS
• DP(다이나믹프로그래밍)

문제풀이

이번 NTS코테 2번과 유사한 문제인데 나한테는 상당히 어렵다...

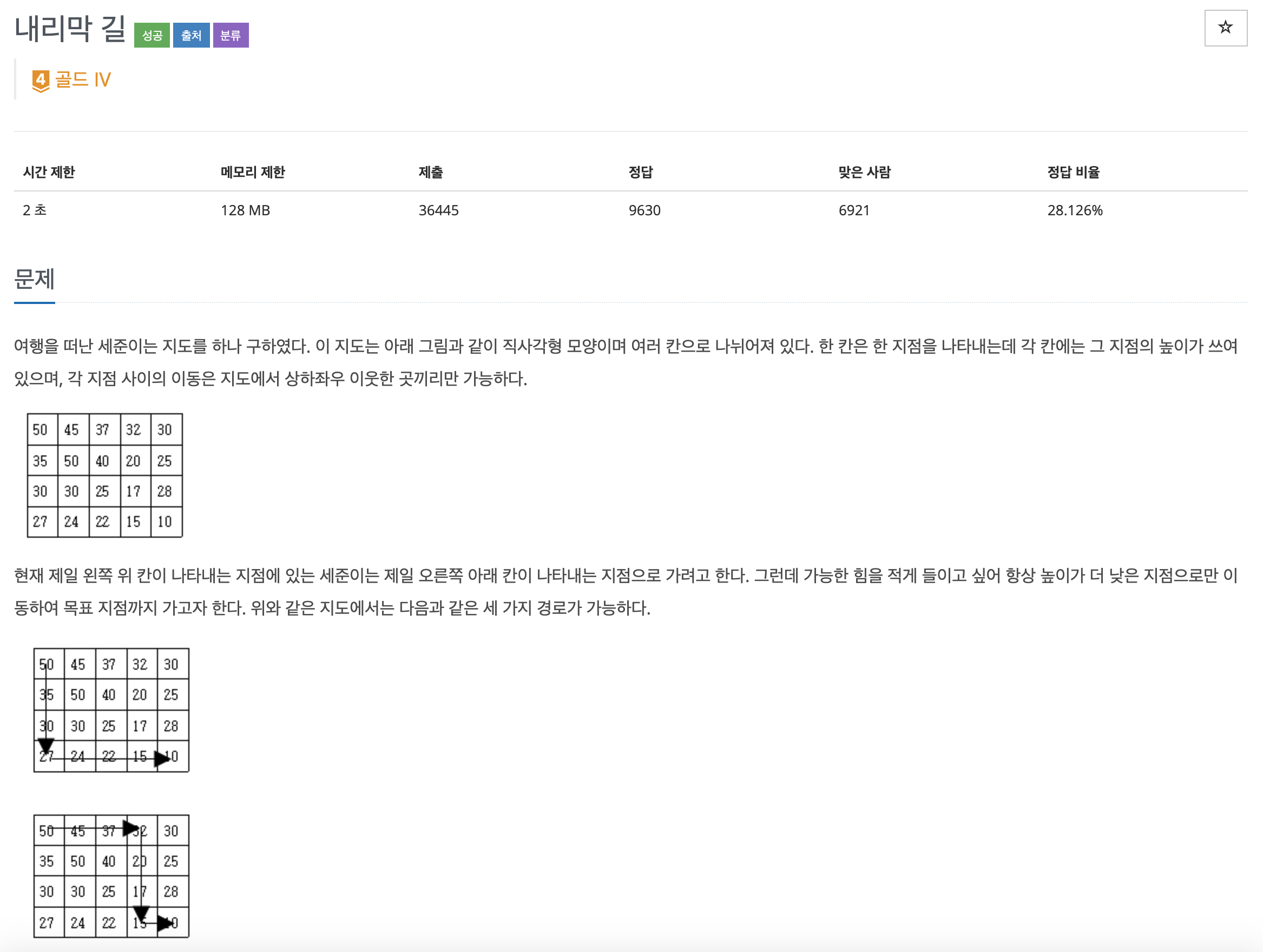
예제에서 만약 50에서 17까지의 갈 수 있는 경로의 수는 17의 상하좌우 중 17보다 큰 20,25,28까지 갈 수 있는 경로의 수 합이다.

이 생각을 떠올리면 17~50까지의 경로라는 문제는 25~50, 20~50, 28~50의 경로의 수인 작은 부분문제의 합으로 나눌 수 있는 DP문제이다.

참고: https://simsimjae.tistory.com/23

도착지점에서부터 시작해 상하좌우를 살펴 해당 지점보다 값이 큰 경우까지의 경로의 수를 계속해서 찾아나가면 된다..

아직 익숙하지 않아 이해가 어려웠다.
관련 알고리즘 문제를 다양하게 풀어봐야겠다.

소스코드

import sys
input = sys.stdin.readline
sys.setrecursionlimit(10000)
m,n=map(int, input().split())
maps=[list(map(int,input().split())) for _ in range(m)]
dx=[1,-1,0,0]
dy=[0,0,1,-1]

dp=[[-1]*n for _ in range(m)]

def dfs(x,y):
    if x==0 and y==0:
        return 1
    if dp[x][y]==-1:
        dp[x][y]=0
        for i in range(4):
            nx=x+dx[i]
            ny=y+dy[i]
            if nx<0 or nx>=m or ny<0 or ny>=n:
                continue
            elif maps[x][y]<maps[nx][ny]:
                dp[x][y]+=dfs(nx,ny)

    return dp[x][y]

print(dfs(m-1,n-1))