접근
오늘 알고리즘 문제는 제시간에 풀기 실패했다.
이 문제는 결국 순서가 지켜질 때
두 개의 집합에 가장 긴 공통된 부분집합의 길이를 구하는 문제라고 볼 수 있다.
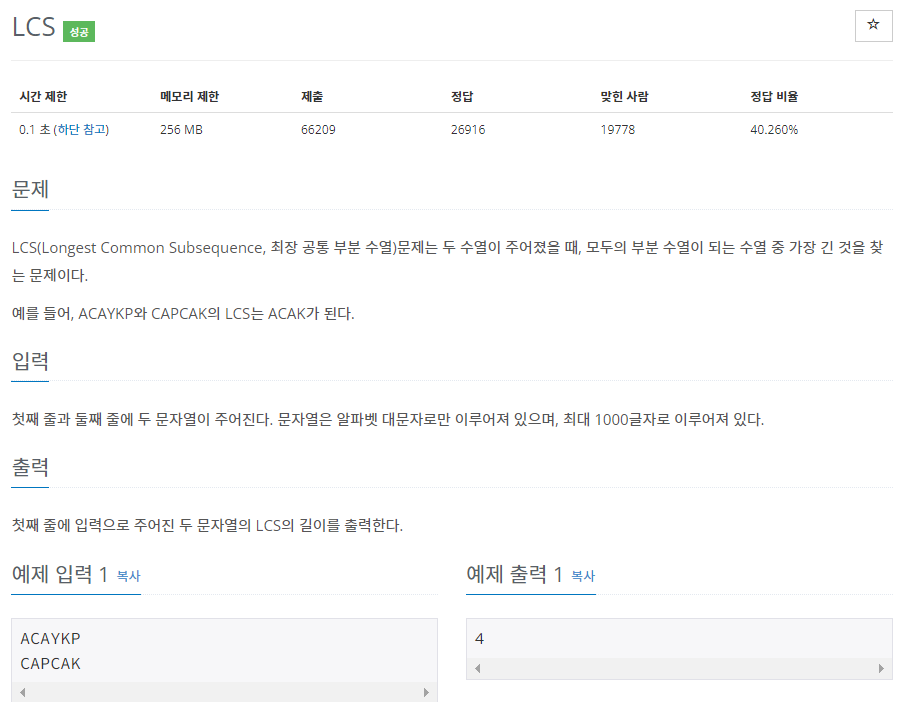
시간 제한이 0.1초이고
최대 글자는 1000자이다.
따라서 3중 for문을 통해서 돌면 10억번의 연산으로 인해 1초를 초과할 것이다.
따라서 2중 for문 내에서 해결해야 한다.
일단 모든 부분집합을 만드는 방법인 DFS의 백트래킹을 이용할 것인가를 고려할 수 있다.
그렇다면
input으로 들어오는 String에 대해 각자 부분집합을 만드는 DFS를 만들고
이 결과물을 저장한 다음에
둘의 저장된 결과물을 비교해서 가장 긴 공통된 부분집합을 찾는다로 접근할 수 있을거 같다.
하지만 LCS는 동적 계획법의 메모제이션을 사용해서 답을 구하는 것이 더 적절한 방법이라고 한다. 또한 이 방법이 더 간결하다.
따라서 동적 계획법을 이용해서 문제를 풀기로 한다.
방법
ACAYKP
CAPCAK
예시를 통해서 문제를 풀어나간다.
-
먼저 아래와 같이 2차원 배열을 만든다.
2중 for문을 통해서 2차원 배열을 채워나갈 것이다. (0.1의 시간 제한에 무리가 없다.)

-
열을 중심으로 채워나가는데 {A}라는 부분집합과 공통의 요소가 있을 때 그 개수를 누적하는 것이다.
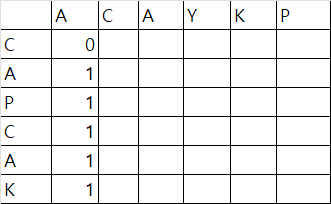
순서대로 계산해보면
{A}와 {C}의 공통 개수 : 0
{A}와 {C,A}의 공통 개수 :1
{A}와 {C,A,P}의 공통 개수 : 1
{A}와 {C,A,P,C}의 공통 개수 : 1
{A}와 {C,A,P,C,A}의 공통 개수 :1
{A}와 {C,A,P,C,A,K}의 공통 개수 :1 -
계속 계산한다.
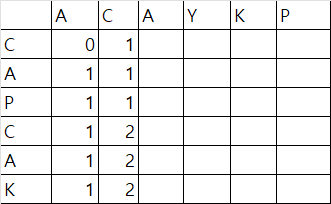
{A,C}와 {C}의 공통 개수 : 1
{A,C}와 {C,A}의 공통 개수 :1
{A,C}와 {C,A,P}의 공통 개수 : 1
{A,C}와 {C,A,P,C}의 공통 개수 : 2
{A,C}와 {C,A,P,C,A}의 공통 개수 :2
{A,C}와 {C,A,P,C,A,K}의 공통 개수 :2 -
이제 무언가 규칙이 보이는데
결국 A->A,C->A,C,A... 이런식으로 추가하면서 검사하는 것이
과거의 결과를 바탕으로 개수가 정해지는 것을 확인할 수 있다.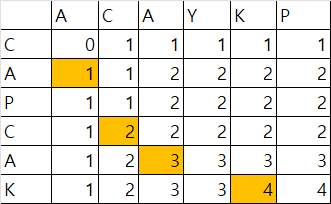
주황색으로 칠해진 부분에서 1이 더해진다.
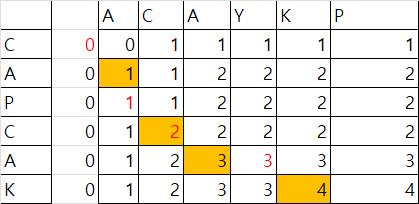
이는 공통된 원소를 동시에 추가하는 과정에서 1이 더해지는 것이고 이 수는 과거 둘다 공통된 요소가 없었을 때인 빨간색으로 칠해진 숫자의 상황에서 +1이 더해진 것이다. 따라서
ACAYKP.charAt(i)==CAPCPK.charAt(j) 경우,
dp[i][j]=dp[i-1][j-1]+1이라는 것을 확인 할 수 있다.
-
또한 같지 않는 경우에는
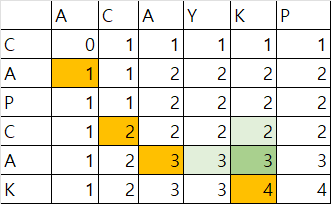
초록색으로 표시된 부분에 알 수 있듯이 과거의 경우에서 가장큰 값이 저장된다.
dp[i][j] = Math.max(dp[i][j-1],dp[i-1][j])
풀이(자바코드)
import java.util.*;
import java.io.*;
public class Main{
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
String A = br.readLine();
String B = br.readLine();
int[][] dp = new int[B.length()+1][A.length()+1];
for(int i=1;i<=A.length();i++){
char a = A.charAt(i-1);
for(int j=1;j<=B.length();j++){
if(a==B.charAt(j-1)){
dp[j][i] =dp[j-1][i-1]+1;
}
else{
dp[j][i] = Math.max(dp[j][i-1],dp[j-1][i]);
}
}
}
bw.write(Integer.toString(dp[B.length()][A.length()]));
bw.flush();
bw.close();
br.close();
}
}