B-tree
B-트리를 알기전에 먼저 이진탐색트리(BST)를 알면 이해하기 쉬울것이다.
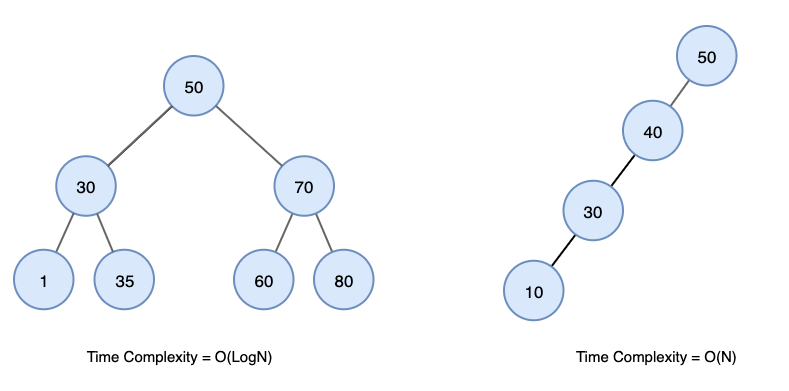
BST는 이진 트리 기반의 탐색을 위한 자료구조이다.
BST는 평균적으로 삽입할때 O(logn)의 시간복잡도가 걸리고 탐색할 때 O(logn)만큼의 시간이 걸릴 것이다. 하지만 삽입을 하는 순서에 따라서 최악의 경우 O(n)만큼의 시간이 걸릴 수가 있다.
이러한 단점을 보완하기 위해서 B-트리를 사용하는데, B-트리는 BST와 달리 하나의 노드에 여러개의 키값을 가질 수 있고 여러개의 자식노드를 가질 수 있으며 탐색의 경우 항상 O(logn)만큼의 시간복잡도를 갖는다는 특징이 있다.
B-트리를 사용하기 위해서 최대차수(M)를 먼저 정해야 하는데,
M : 각 노드의 최대 자녀노드 수
M-1 : 각 노드의 최대 키수
(M/2)반올림 : 각 노드의 최소 자녀노드 수
(M/2)반올림 - 1 : 각 노드의 최소 키수
각 노드에 연결되는 자녀노드 수는 최대 M만큼 가질 수 있고 만약 자녀노드수가 M개라면 해당 노드의 키 값은 M-1개로 고정되어 있다. 예시로 4개의 자녀노드를 갖고있다면 해당 노드의 키 갯수는 3개가 될 것이다.
그리고 최소 '(M/2)반올림 - 1'개 만큼의 키를 가지고 있어야 한다. 만약 최대차수가 5이고 어떤 노드의 키 갯수가 1개라면, 최소 2개만큼 키를 가지고 있어야 하므로 재배치가 필요할 것이다.
노드에 키를 삽입할 때의 규칙들을 보자면
1. 추가는 항상 적절할 위치인 Leap노드에 한다.
2. 노드가 넘치면 가운데를 기준으로 좌우 key들을 분할하고 가운데key는 부모노드로 간다.
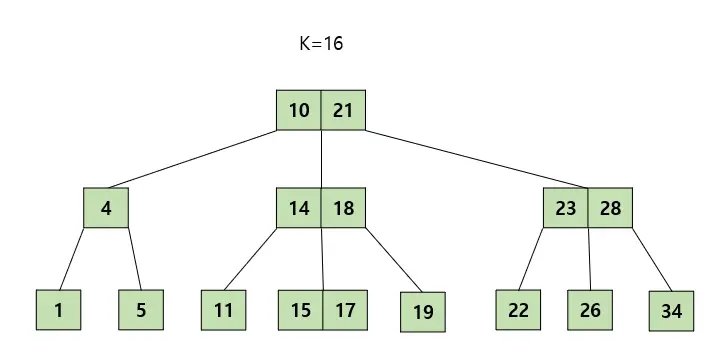
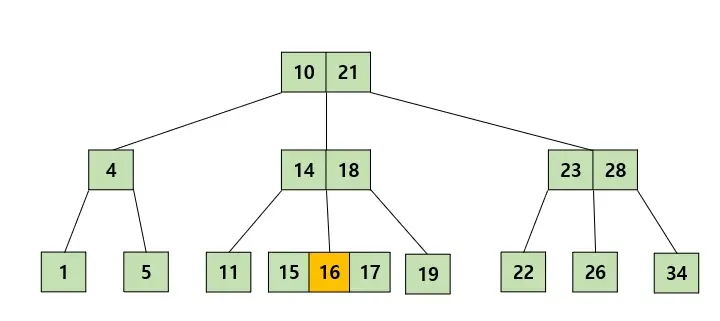
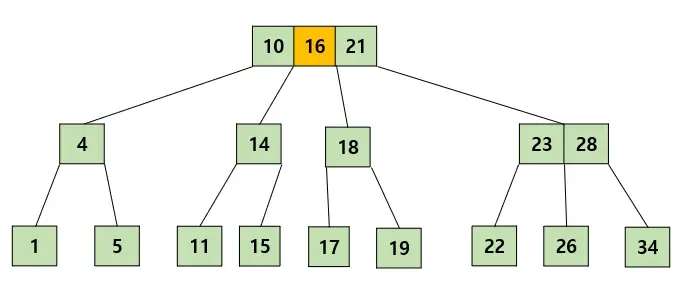
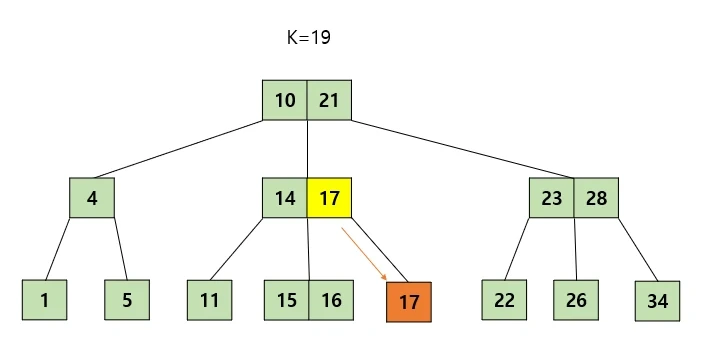
예를 들어 이 그림에서 16을 삽입한다고 가정하자. 맨 처음 리프노드의 자기자리(15와 17사이)를 찾고 그 자리에 삽입을 할 것이다.
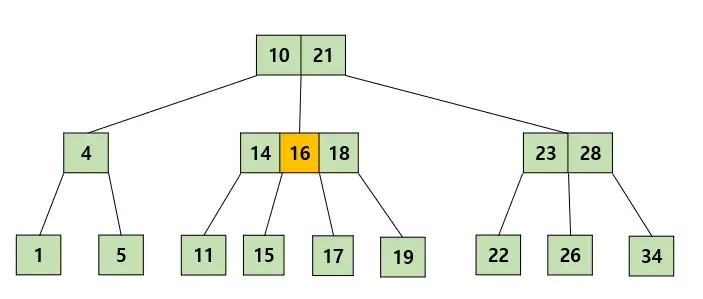
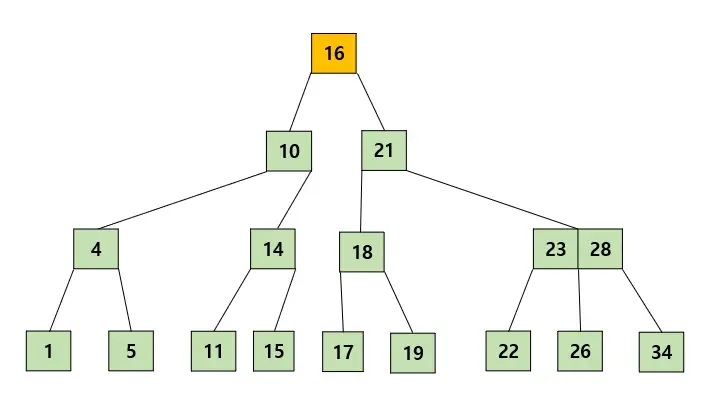
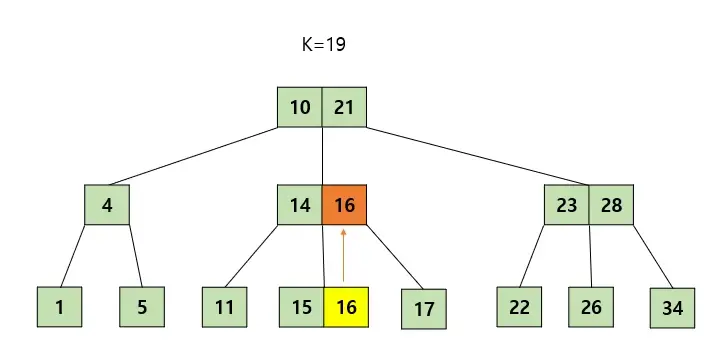
그러면 최대 가질 수 있는 키 수를 넘었으므로 2번규칙에 의해 가운데인 16을 기준으로 15,17이 각각 16의 왼쪽, 오른쪽 자식으로 나뉘어지고 16은 부모노드로 올라갈 것이다.
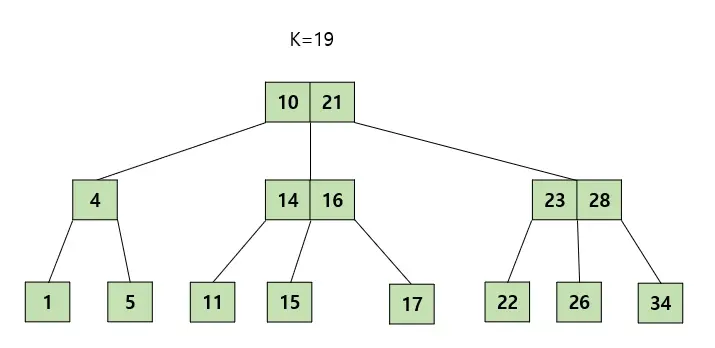
부모노드로 올라가서도 키 수를 넘었기 때문에 같은 원리로 반복을 해준다. 그리고 만약 부모노드가 비어있다면 새롭게 노드를 만들어준다. 최종적으로 모든 노드가 적절한 상태에 있으므로 삽입을 종료한다.
노드에서 키를 삭제할 경우의 규칙들은 삽입때보다 더 복잡해진다.
<삭제할 노드가 Leap노드일 경우>
1. 삭제도 항상 Leap노드에서 한다.
2. 삭제후 최소 key수보다 작아졌다면?
-> 1. key수가 여유로운 형제의 지원을 받는다.
-> 2. 1번이 불가능하다면 부모의 지원들 받고 형제와 합친다.
-> 3. 2번후 부모노드에 문제가 있다면 다시 1번부터.
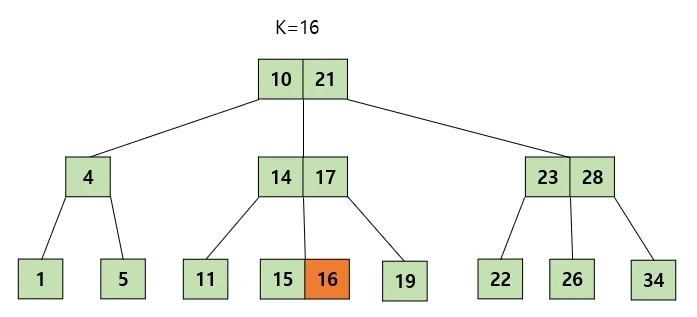
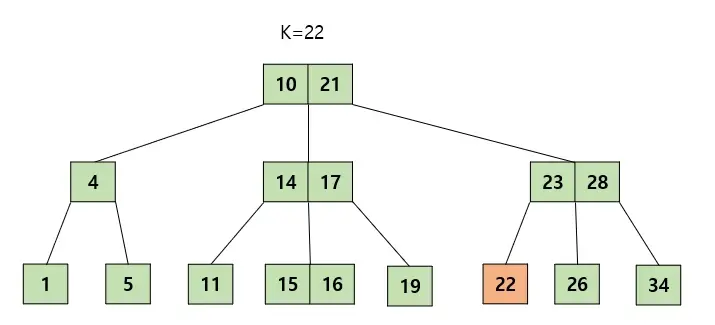
위 그림에서 16을 삭제한다고 가정해 보자, 이 경우에는 삭제를 해도 최소 키 갯수인 1개를 만족하므로 삭제해주고 다른 조치를 취하지 않아도 된다.
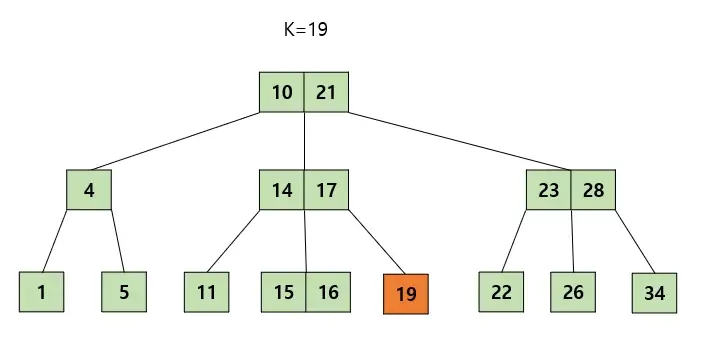
만약 19 삭제 후 최소 키값을 만족하지 못한다면, 2.1에 있는 규칙을 적용하면 된다. 따라서 형제( 같은 부모노드아래 있는 노드중 옆에 있는 노드)노드에 값을 빌려오면 된다. 바로 16을 빌려오면 트리에 문제가 생길것이다. 그러므로 형제노드에 있는 16을 부모노드로 옮겨주고 부모노드에 있는 노드를 해당 노드로 가져오면 된다.
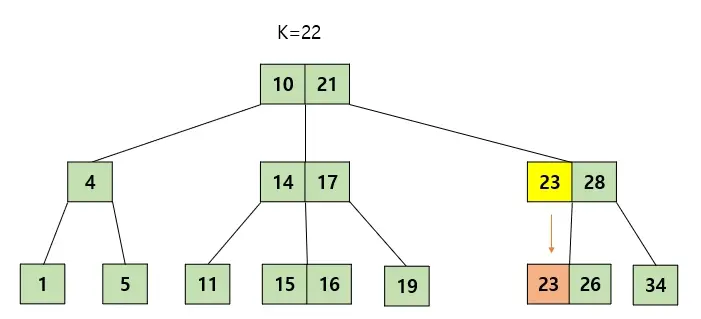
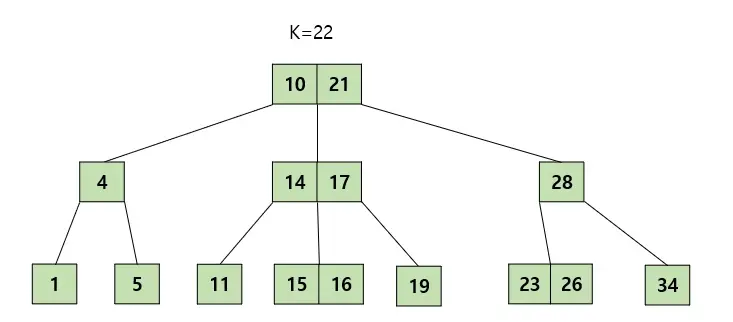
22키를 삭제한다고 가정해보자. 22를 삭제하면 최소키값을 만족하지 못하게 된다. 그래서 형제노드를 봤는데 나에게 빌려줄 형편이 되지 못하는것 같다. 그래서 2.2 규칙을 적용할 것이다. 우선 22를 삭제해주고 부모노드를 빌려와서 옆에 형제노드와 합쳐주면 22 제거가 끝난다.
<삭제할 노드가 Leap노드가 아닐 경우>
1. Leap노드에 있는 데이터중 적절한 데이터와 위치를 바꾼다.
2. Leap노드에서 삭제하고 필요시 재조정
1번규칙에 있는 '적절한 데이터'는 바로 삭제하려는 값과 가장 가까운 데이터를 말한다. 그래서 가장 가까운 데이터는 어떻게 찾냐면 데이터 기준으로 왼쪽에는 자신보다 작은 값들만 있을것이다. 마찬가지로 오른쪽에는 큰 값들만 있을 것이다. 그렇다면 다신보다 작은 수들중 제일 큰수 또는 자신보다 큰수들중 가장 작은수가 적절한 값이 될 것이고 왼쪽노드에서 제일 오른쪽으로 가면 작은것들중 큰 수가 있을것이고 오른쪽노드에서 제일 왼쪽으로 가주면 큰것들중 가장 작은 수가 있을것이다.
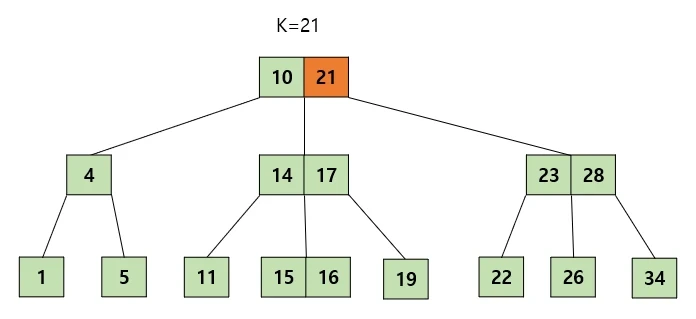
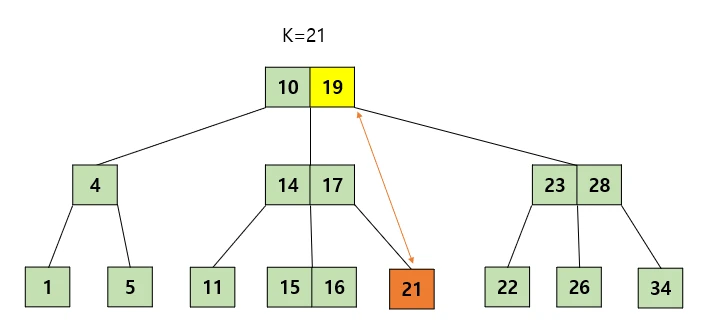
21을 삭제한다고 가정해보자. 이 그림에서는 작은수들중 제일 큰수를 적절할 데이터로 잡았다. 그 수와 swap을 해주고 swap한 자리에서 삭제하려는 키를 삭제해주면 된다.
여기서 만약에 최소 키 갯수를 만족하지 못한다면 다시 <삭제할 노드가 Leap노드일 경우>의 규칙들을 따라주면 될 것이다.
만약 B-트리의 로직에 대해 더 공부하고싶다면 아래 링크에 들어가서 어떤 로직으로 돌아가는지 확인하길 바란다.
B트리 로직
그림 출처