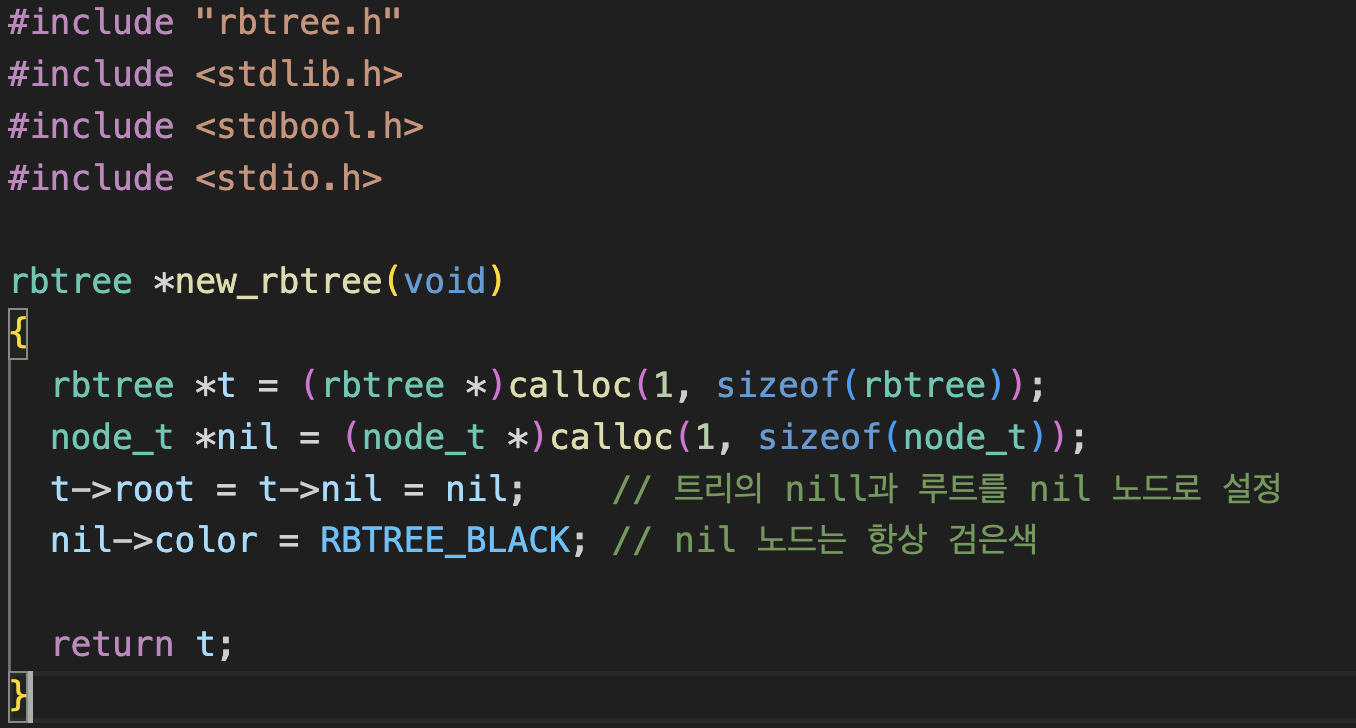
트리 생성
C언어는 기본적으로 bool자료형이 없기때문에 헤더파일로 stdbool을 선언해 주었다.
그리고 모든 리프노드의 자식을 nil로 연결해 주는 방식으로 rb트리를 생성 해 주었다.
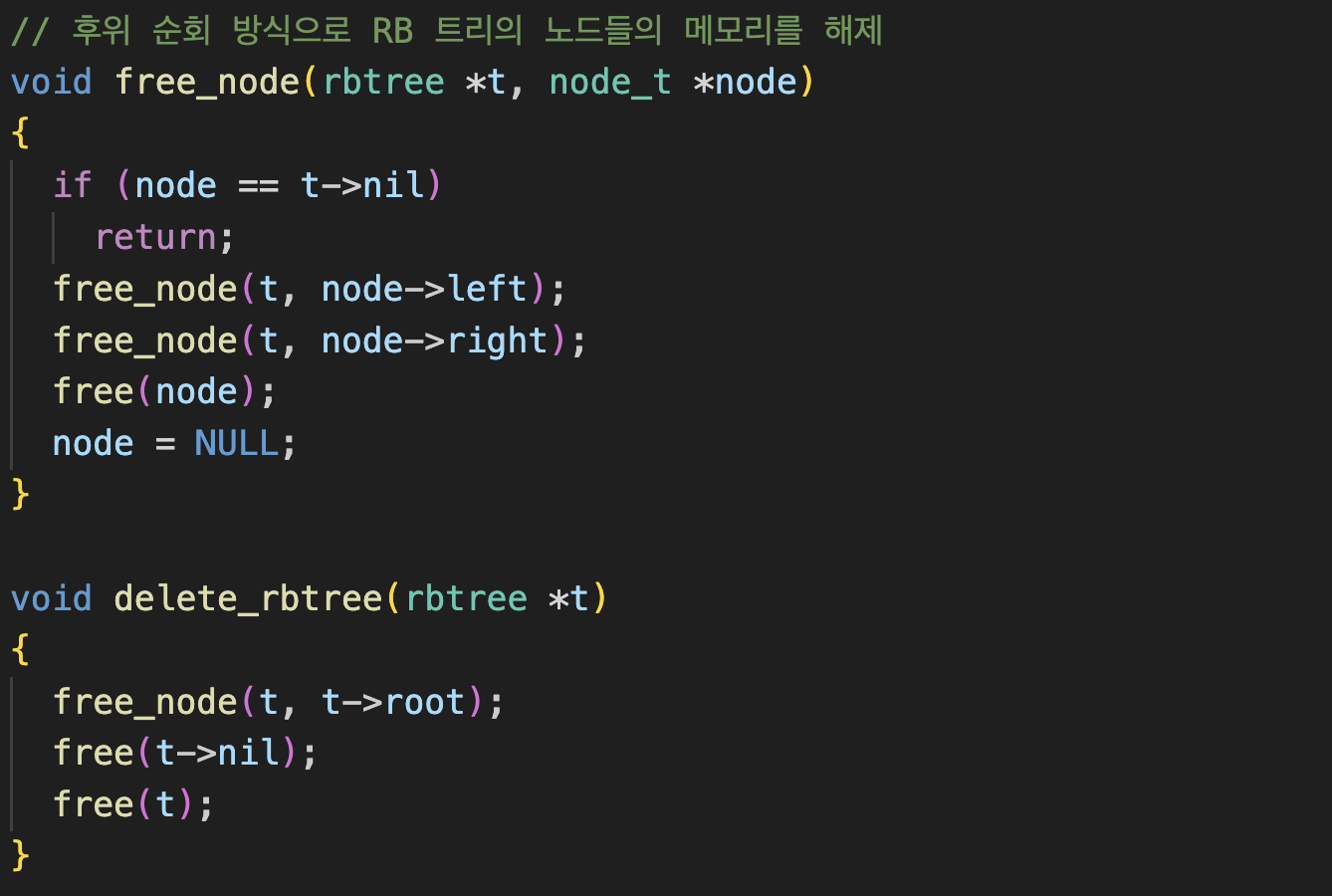
트리 전체삭제
트리삭제 함수를 재귀적으로 만들어주었다. 후위탐색을 참고하여 만들었는데, 전위나 중위순회로 탐색하면서 삭제해 주면 이미 right나 left로 가기전에 노드가 삭제되어버리기 때문에 왼쪽, 오른쪽 전부 탬삭 한 뒤에 마지막에 노드를 삭제(free)해 주었다.
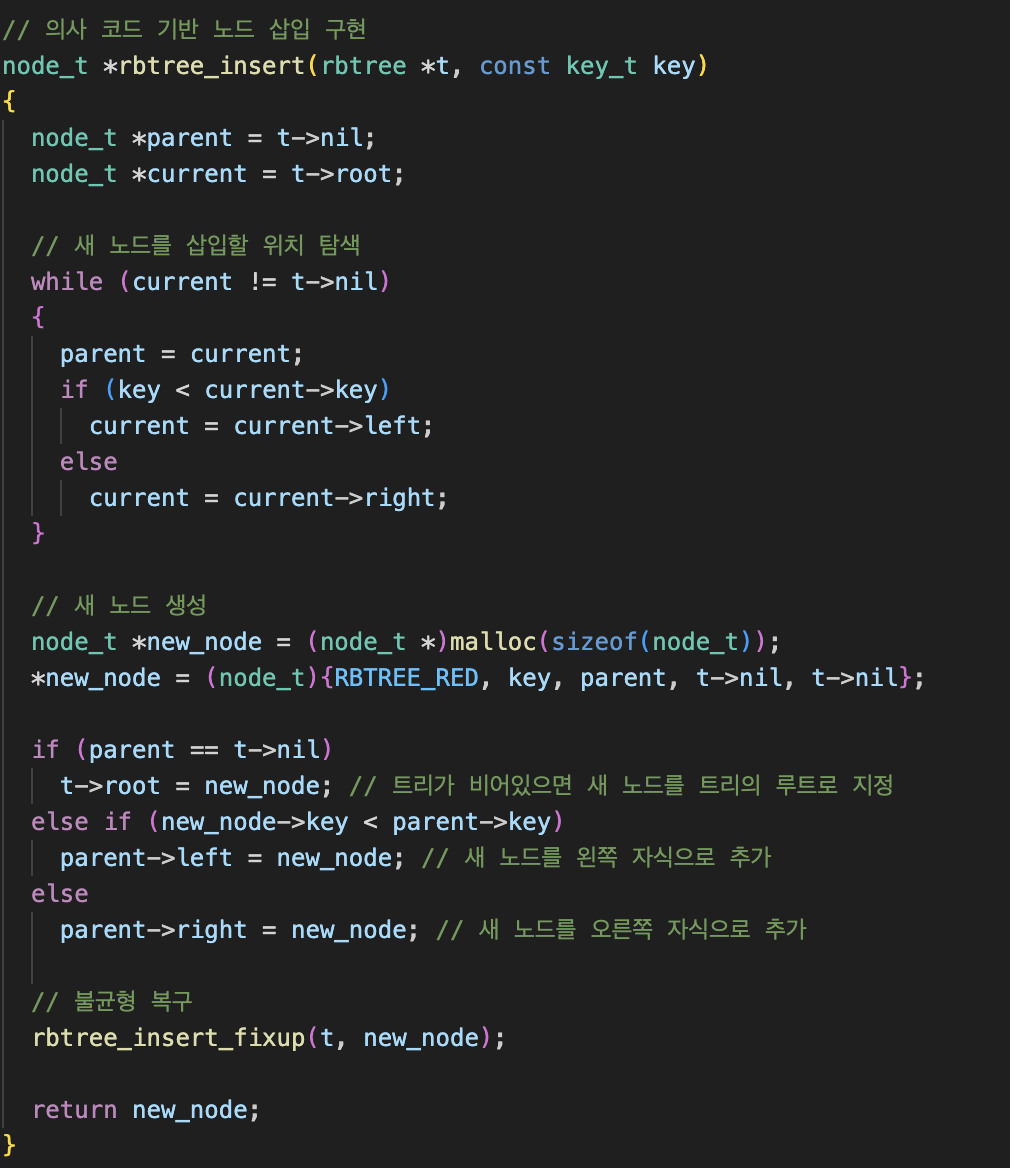
노드 삽입
RB트리의 삽입은 BST와 비슷하다.
BST와 다른 점은 삽입 후에 규칙에 어긋나게 되면 트리를 fixup해주어야 한다는 점이다.
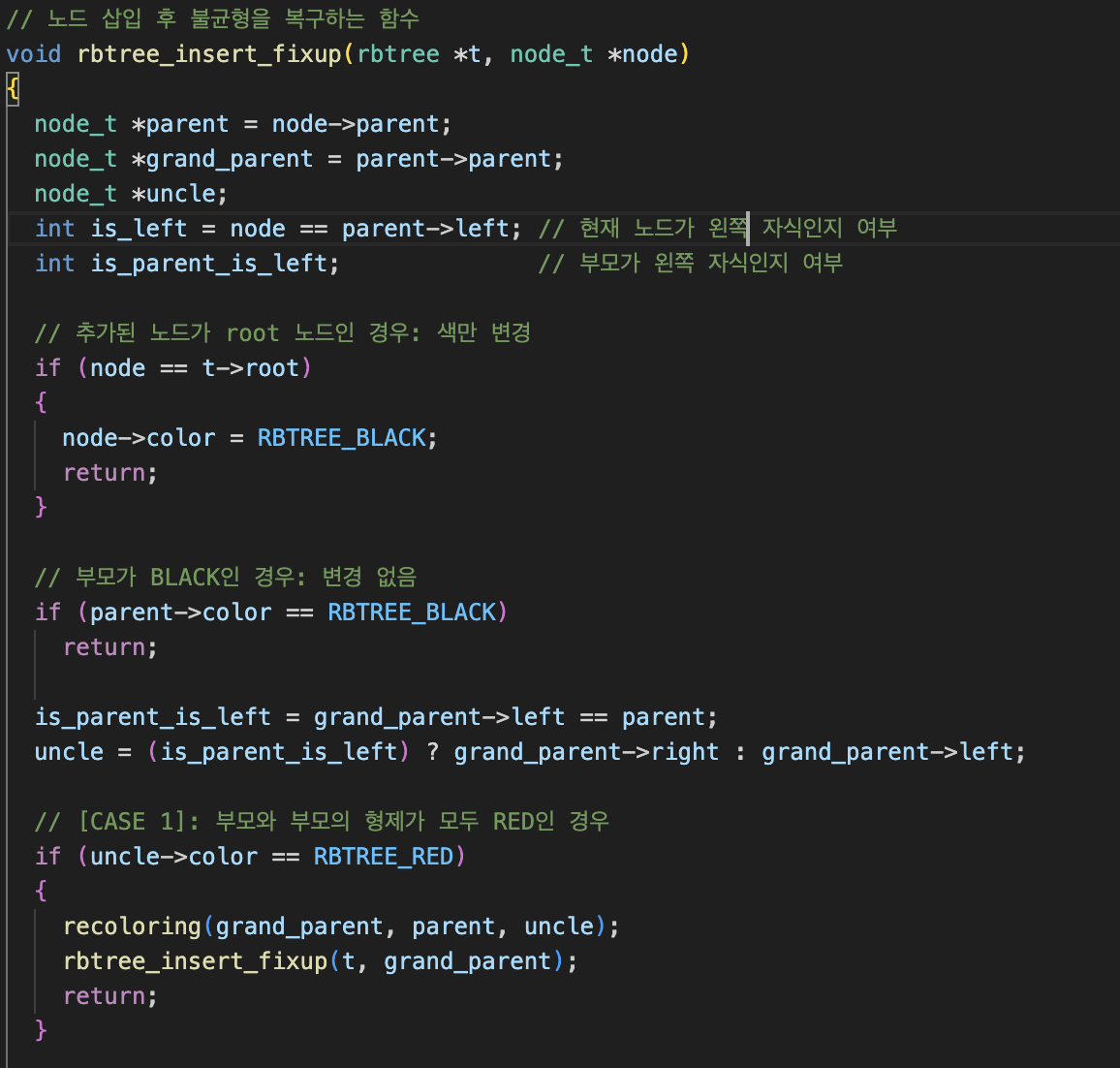
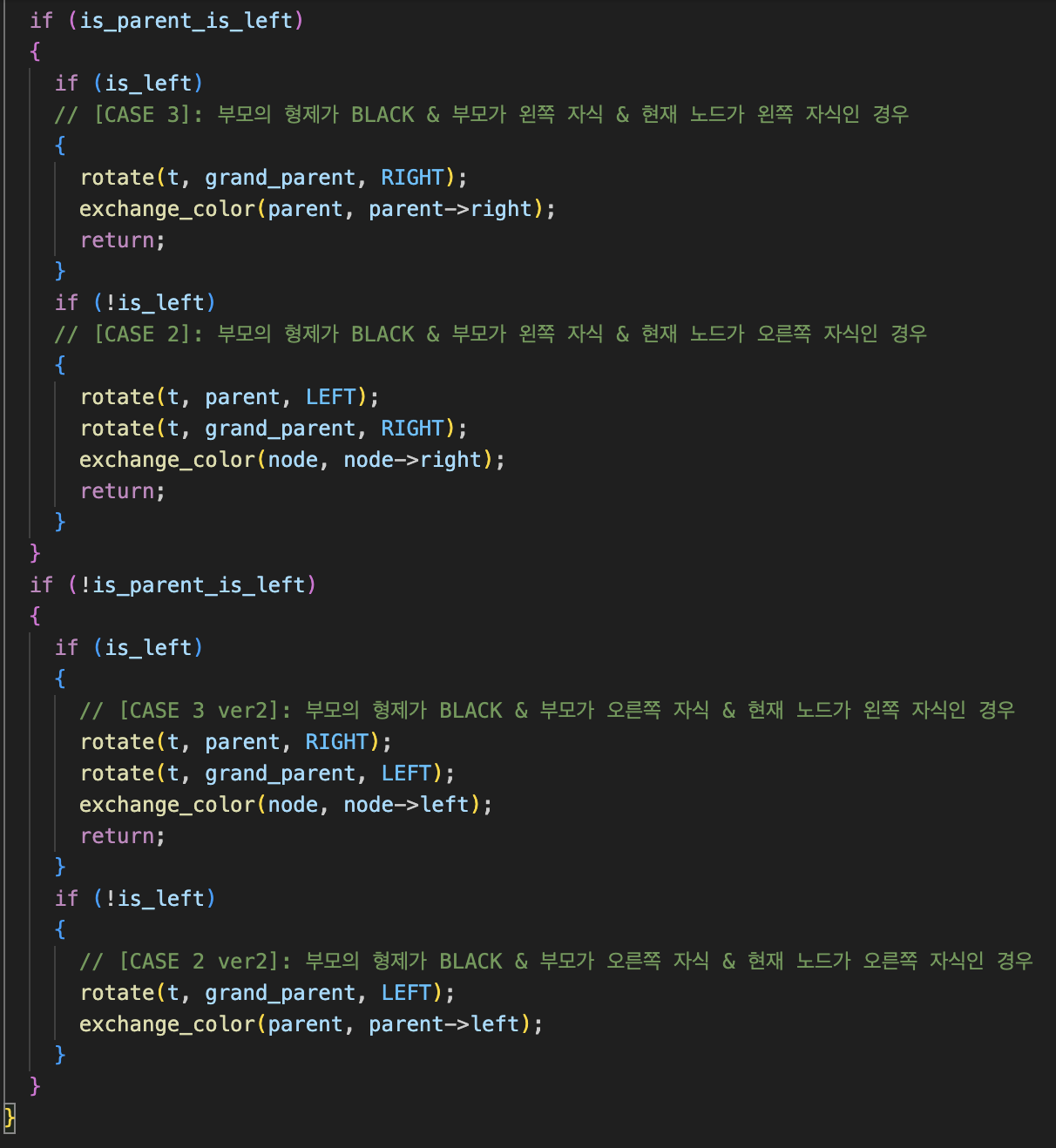
삽입시 트리 불균형 복구
불균형 복구 규칙에 따라 나누어서 코드를 짜주었다.
삽입노드의 부모가 조부모의 왼쪽자식이냐, 오른쪽 자식이냐, 그리고 삽입 노드가 부모의 왼쪽 자식이냐, 오른쪽 자식이냐에 따라 어디로 회전할 지 달라지는데, 나는 기준을 if문을 이용해 총 네 가지로 나누어서 코드를 짜주었다.
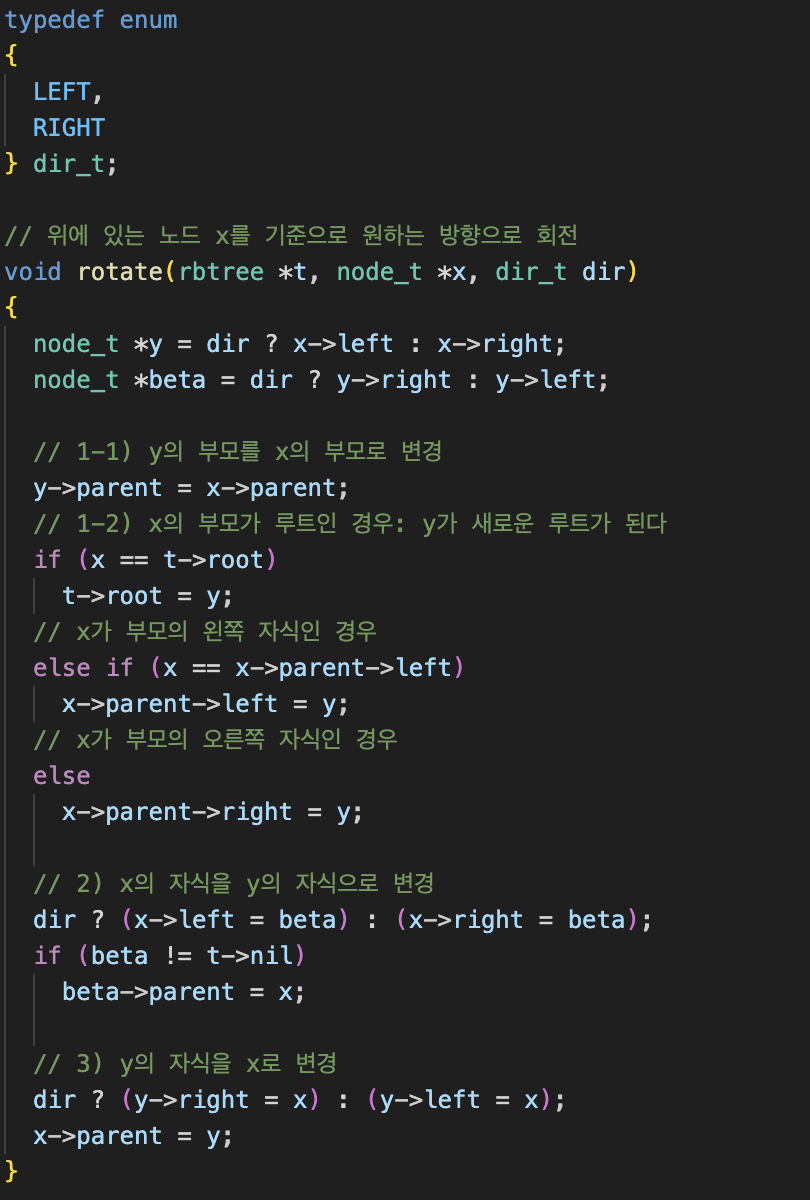
회전
회전 부분은 같은 팀원분이 짰는데, 다른팀들은 오른쪽회전, 왼쪽회전 두 개의 함수를 만들어 각각 상황에 맞게 함수를 사용하였다.
우리는 하나의 함수로 합쳐서 왼쪽으로 회전할 것인지, 오른쪽으로 회전할 것인지 인자로 받아와 함수안에서 삼항연산자를 이용해서 처리하였다.
색 바꾸기
색 바꾸는 함수는 여러곳에서 많이 쓰인다. 색바꿔주는 부분을 같은 함수 안에 넣어준다면 코드길이가 길어지기 때문에 함수 밖으로 빼주어 코드길이를 줄여주었다.
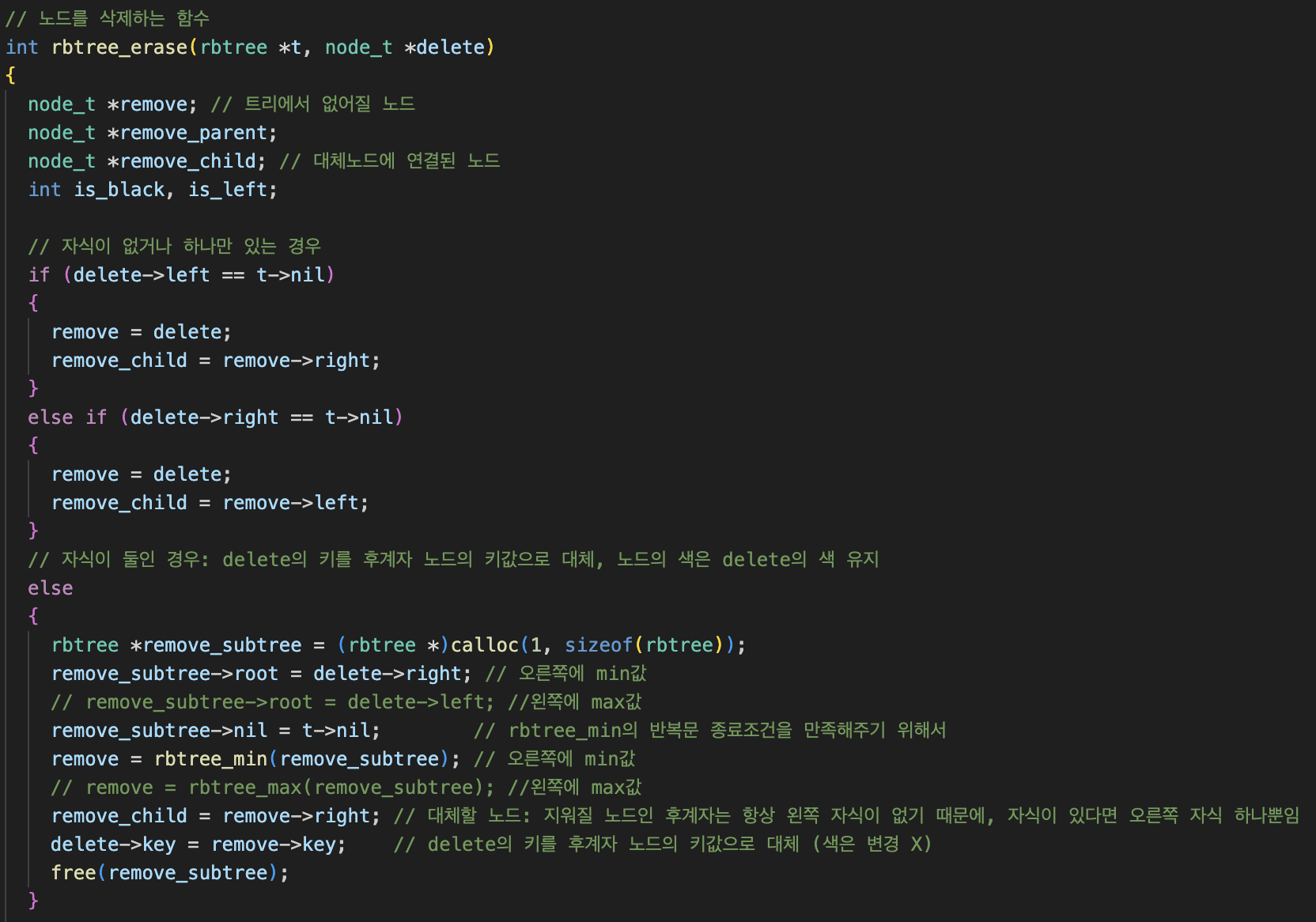
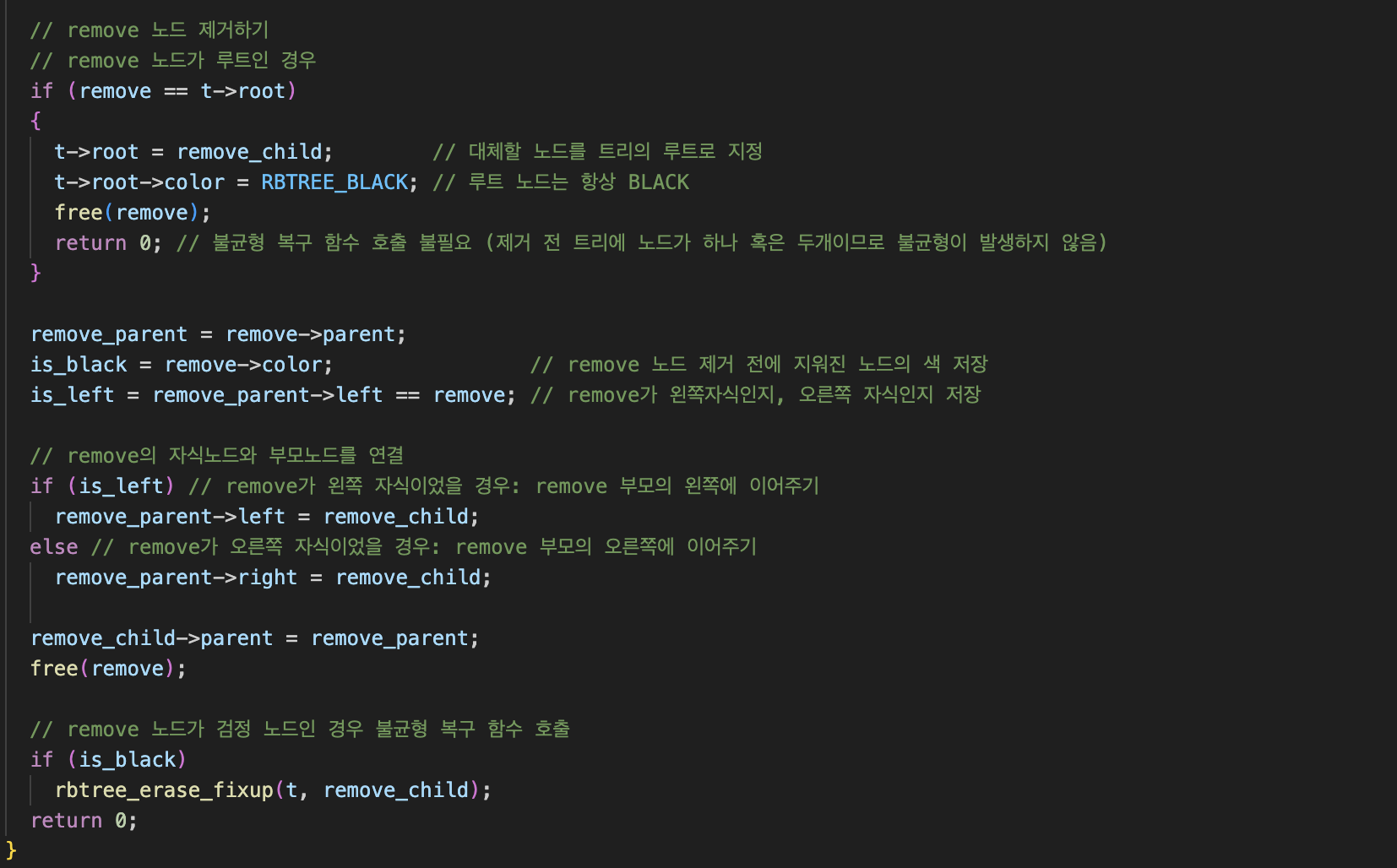
노드 삭제
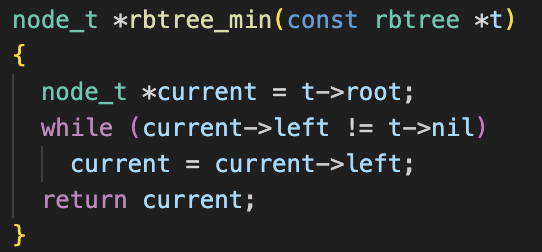
삭제부분도 삽입과 마찬가지로 BST기반으로 삭제를 해 주면 된다. 내 코드에서는 후계자노드를 찾을 때 rbtree_min함수를 활용했다.
그런데, rbtree_min함수는 인자로 노드를 주는것이 아닌 트리를 줘야한다. 그래서 오른쪽 서브트리를 루트노드로 하는 트리를 만들어 인자로 주었다.
여기서 새 트리를 만들 때 동적할당을 해 주었기 때문에 테스트코드를 돌렸을 때 다른 팀보다 메모리할당을 5000바이트정도 더 해주고 할당해제도 5000바이트 더 해주게 되었다.
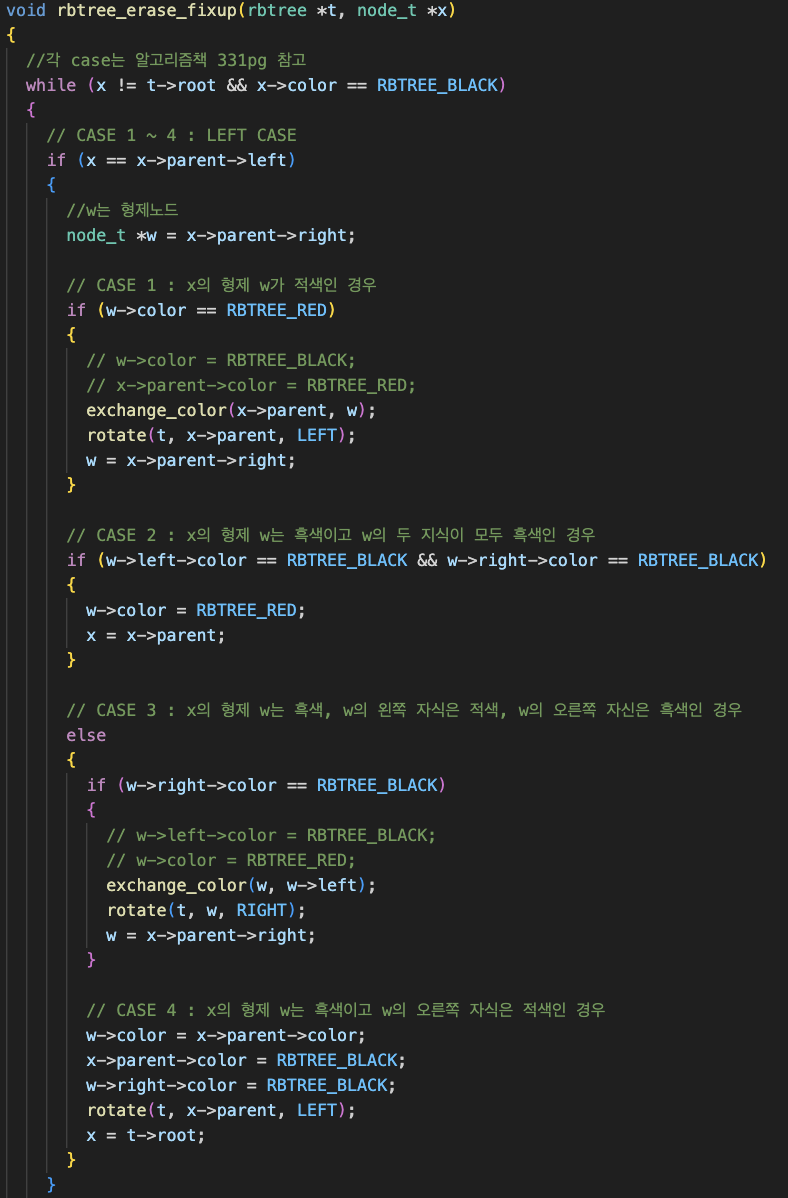
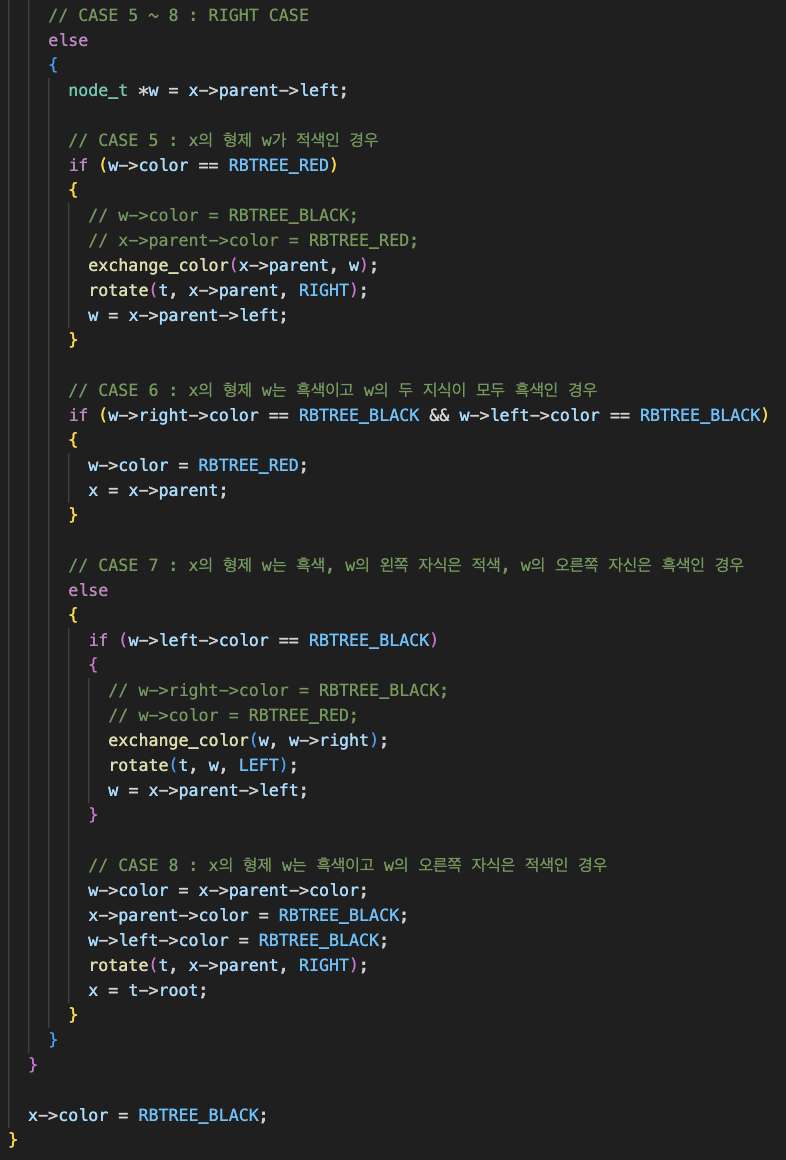
삭제시 트리 불균형 복구
삭제시 불균형 복구할 때의 규칙은 크게 네 가지로 볼 수 있는데,
1. 삭제자리의 형제가 적색일 경우
2. 삭제자리의 형제가 흑색이고 그 형제의 자식 모두 흑색일 경우
3. 삭제자리의 형제가 흑색이고 형제의 왼쪽자식은 적색, 오른쪽 자식은 흑색인 경우
4. 제자리의 형제가 흑색이고 형제의 오른쪽 자식이 적색인 경우
여기서 자신의 위치가 부모의 오른쪽 자식 또는 왼쪽 자식인지도 고려해야한다. 따라서 총 8개의 경우로 코드를 짰다.
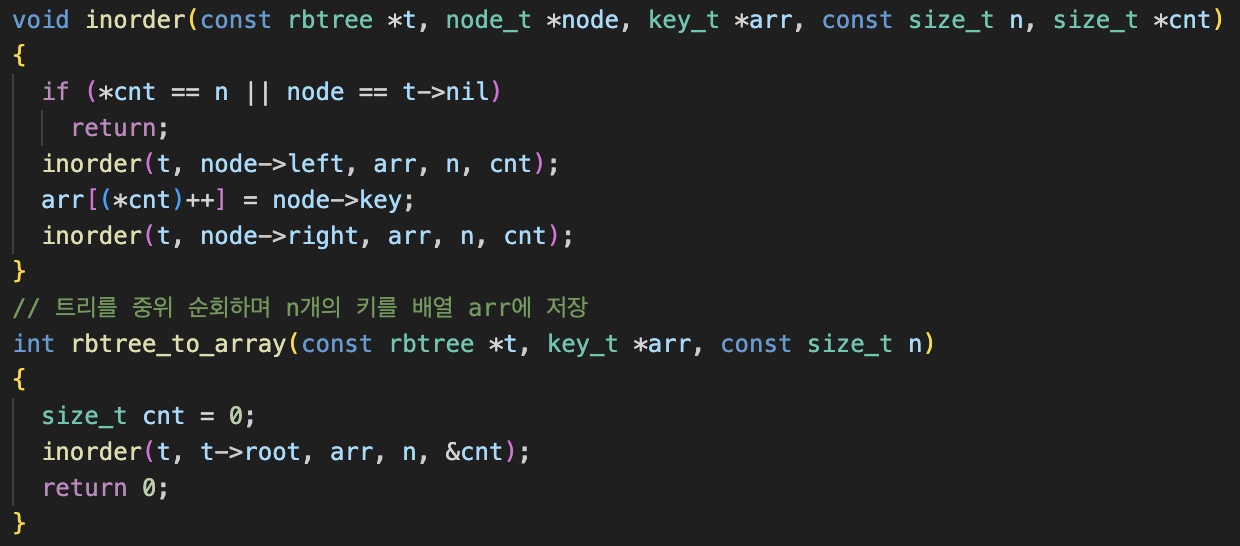
RB트리를 오름차순으로 배열에 저장
반복문으로 코드를 짜게 된다면 inorder함수를 따로 정의하지 않아도 되겠지만 이전에 트리순회를 순환호출로 짜봤는데 RB트리 역시 순환호출로 배열에 저장하는 법 말고는 반복적으로 푸는 방법이 떠오르지 않았다.
따라서 중위순회의 print하는 자리에 배열에 저장하는 방식으로 코드를 짰다.
실행 결과