[백준] 1167번 트리의 지름 - Python / 알고리즘 기초 2/2 - 트리 1

ByungJik_Oh·2025년 4월 26일

Baekjoon Online Judge

[Baekjoon Online Judge]

목록 보기

124/244

💡 문제

트리의 지름이란, 트리에서 임의의 두 점 사이의 거리 중 가장 긴 것을 말한다. 트리의 지름을 구하는 프로그램을 작성하시오.

입력

트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지 매겨져 있다.

먼저 정점 번호가 주어지고, 이어서 연결된 간선의 정보를 의미하는 정수가 두 개씩 주어지는데, 하나는 정점번호, 다른 하나는 그 정점까지의 거리이다. 예를 들어 네 번째 줄의 경우 정점 3은 정점 1과 거리가 2인 간선으로 연결되어 있고, 정점 4와는 거리가 3인 간선으로 연결되어 있는 것을 보여준다. 각 줄의 마지막에는 -1이 입력으로 주어진다. 주어지는 거리는 모두 10,000 이하의 자연수이다.

출력

첫째 줄에 트리의 지름을 출력한다.

💭 접근

우선 이 문제는 모든 정점에서의 각 정점까지의 거리를 구하고, 이 중 가장 큰 값을 출력하면 될 것 같지만, 입력의 최대가 100,000이므로 플로이드 워셜 알고리즘을 사용할 수 없다. 따라서 다른 방법을 사용해야 한다.

우선 트리의 지름을 이해하기 위해 1967번 트리의 지름 문제에 있는 그림을 참고하면 된다.

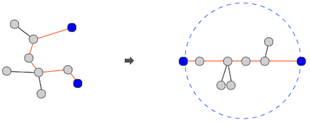
이 그림처럼 트리의 어떤 두 정점을 잡고 쭉 늘렸을 때 모든 정점이 원 안에 들어온다면 이 두 정점 사이의 거리를 트리의 지름이라고 한다.

이때 트리의 지름을 구하기 위해서 한가지 더 알아야할 것이 있는데, 임의의 한 정점에서 가장 멀리 떨어져 있는 정점은 반드시 트리의 지름을 구성하는 두 정점 중 하나라는 것이다.

다시 말해, 임의의 한 정점에서 가장 멀리 떨어져 있는 정점을 찾은 뒤, 다시 이 정점에서 가장 멀리 떨어져 있는 정점 또한 트리의 지름을 구성하는 또 다른 정점이라는 것이다.

따라서 이 문제를 해결하기 위해서 다음과 같은 순서로 코드를 구현하면 된다.

임의의 한 정점에서 가장 멀리 떨어져있는 정점을 찾는다.
1번에서 찾은 정점에서 가장 멀리 떨어져 있는 정점과의 거리(지름)를 구한다.

📒 코드

import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline

def dfs(start, width):
    global max_width, max_node

    visited[start] = True
    if width > max_width:
        max_width = width
        max_node = start

    for next in tree[start]:
        if not visited[next[0]]:
            visited[next[0]] = True
            dfs(next[0], width + next[1])

v = int(input())
tree = [[] for _ in range(v + 1)]
for _ in range(v):
    node = list(map(int, input().split()))
    for i in range(1, len(node) - 1, 2):
        tree[node[0]].append([node[i], node[i + 1]])

visited = [False for _ in range(v + 1)]
max_width = 0
max_node = None
dfs(1, 0)

visited = [False for _ in range(v + 1)]
max_width = 0
dfs(max_node, 0)
print(max_width)