[백준] 11726번 2xn 타일링 - Python / 알고리즘 기초 1/2 - 다이나믹 프로그래밍 1

---

---

---

💡 문제

2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.

아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.

입력

첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)

출력

첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.

---

💭 접근

도형을 그리는 경우의 수를 그려보면,
n = 1(1가지), 2(2가지) 일때,

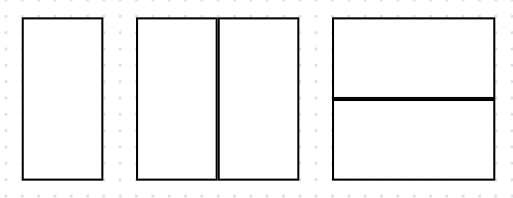
n = 3(3가지) 일때, dp[3] = dp[2] + dp[1]

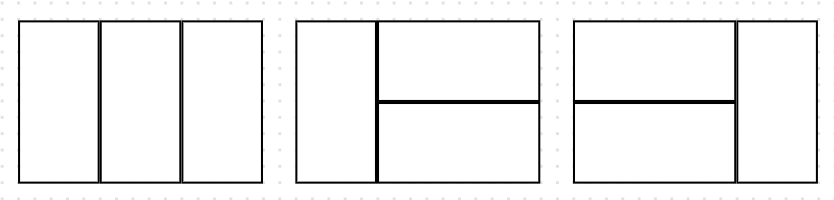
n = 4(5가지) 일때, dp[4] = dp[3] + dp[2]

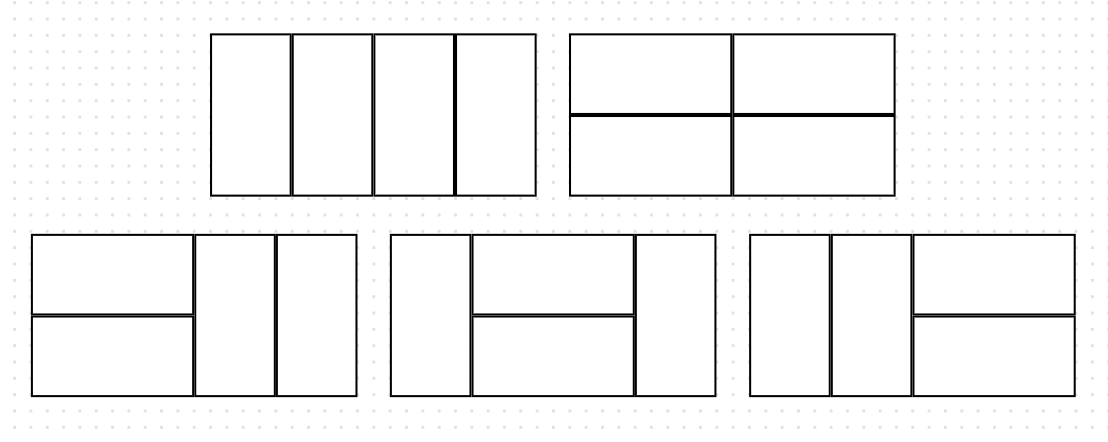
따라서, 점화식은 dp[i] = dp[i - 1] + dp[i - 2] 로 도출해낼 수 있다.

---

📒 코드

n = int(input())
dp = [0, 1, 2]

for i in range(3, n + 1):
    dp.append((dp[i - 1] + dp[i - 2]) % 10007)

print(dp[n])

---

💭 후기

간단하게 경우의 수를 구할 수 있을 땐 직접 구해보며 점화식을 도출하는 것도 좋은 방법인 것 같다.

---

🔗 문제 출처

https://www.acmicpc.net/problem/11726

---