[백준] 14391번 종이 조각 - Python / 알고리즘 기초 2/2 - 브루트 포스 - 비트마스크

ByungJik_Oh·2025년 4월 14일

[Baekjoon Online Judge]

목록 보기

101/244

💡 문제

영선이는 숫자가 쓰여 있는 직사각형 종이를 가지고 있다. 종이는 1×1 크기의 정사각형 칸으로 나누어져 있고, 숫자는 각 칸에 하나씩 쓰여 있다. 행은 위에서부터 아래까지 번호가 매겨져 있고, 열은 왼쪽부터 오른쪽까지 번호가 매겨져 있다.

영선이는 직사각형을 겹치지 않는 조각으로 자르려고 한다. 각 조각은 크기가 세로나 가로 크기가 1인 직사각형 모양이다. 길이가 N인 조각은 N자리 수로 나타낼 수 있다. 가로 조각은 왼쪽부터 오른쪽까지 수를 이어 붙인 것이고, 세로 조각은 위에서부터 아래까지 수를 이어붙인 것이다.

아래 그림은 4×4 크기의 종이를 자른 한 가지 방법이다.

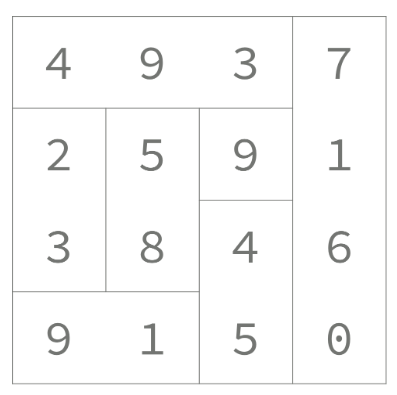
각 조각의 합은 493 + 7160 + 23 + 58 + 9 + 45 + 91 = 7879 이다.

종이를 적절히 잘라서 조각의 합을 최대로 하는 프로그램을 작성하시오.

입력

첫째 줄에 종이 조각의 세로 크기 N과 가로 크기 M이 주어진다. (1 ≤ N, M ≤ 4)

둘째 줄부터 종이 조각이 주어진다. 각 칸에 쓰여 있는 숫자는 0부터 9까지 중 하나이다.

출력

영선이가 얻을 수 있는 점수의 최댓값을 출력한다.

💭 접근

처음 이 문제를 보았을 때 단순히 가로로 자른 종이들의 합과 세로로 자른 종이들의 합을 비교해서 큰 값이 정답이지 않을까 생각하고 이대로 문제를 풀었더니 오답이 나왔다. 이후 반례를 찾아보니,

입력 :
4 4
1000
0001
0000
1000

오답 : 2001
정답 : 2010

이처럼 0이 섞여 있는 경우에 문제가 발생하였고, 비트마스크를 통해 모든 경우의 수를 따져보고 이 중 최댓값을 구해야 한다는 것을 알았다.

따라서 이 문제는 입력으로 주어진 n x m의 2차원 종이를 n x m의 1차원 종이로 생각하고 1과 0으로 이루어진 비트마스크로 탐색을 해야한다.

이때 아래와 같이 코드를 작성하면,

for mask in range(1 << (n * m))

mask는 $0$ ~ $2^{(n \times m)} - 1$ 의 범위를 갖게되는 이진수가 되는데 이를 보기 쉽게 종이에 덧댄다는 생각으로 표로 표현하면,
(n = 4, m = 4 이고, mask = 31 (0000 0000 0001 1111 일 때))

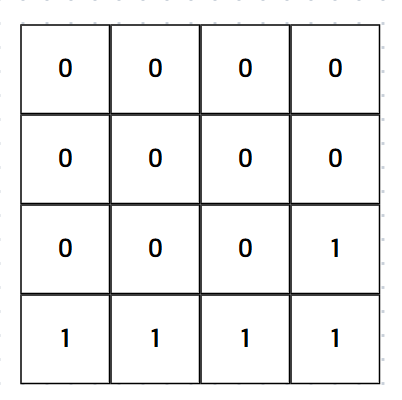
이와 같이 표현할 수 있고, 1은 가로로 이어지는 수, 0은 세로로 이어지는 수로 나타날 수 있다. 이렇게 생성된 마스크에 대해

# 가로 합
        for i in range(n):
            h_sum = 0
            for j in range(m):
                idx = i * m + j # 4, 4 일 때, idx = 0~15
                if mask & (1 << idx) != 0: # 가로일 때
                    h_sum = h_sum * 10 + paper[i][j]
                else: # 세로일 때 초기화
                    sum += h_sum
                    h_sum = 0
            sum += h_sum
        #세로 합
        for j in range(m):
            v_sum = 0
            for i in range(n):
                idx = i * m + j
                if mask & (1 << idx) == 0: # 세로일 때
                    v_sum = v_sum * 10 + paper[i][j]
                else: # 가로 일 때 초기화
                    sum += v_sum
                    v_sum = 0

idx = (0000 0000 0000 0000) ~ (1000 0000 0000 0000) 까지의 비트를 한칸씩 왼쪽으로 Shift을 하며 비트연산을 통해 가로와 세로합을 구하여 최대값을 갱신해주면 된다.

📒 코드

def solve():
    ans = 0
    # 비트마스크로 경우의 수 모두 따져보기
    for mask in range(1 << (n * m)):
        # print(mask) 0 ~ 2^(n*m)-1
        sum = 0
        # 가로 합
        for i in range(n):
            h_sum = 0
            for j in range(m):
                idx = i * m + j # 4, 4 일 때, idx = 0~15
                if mask & (1 << idx) != 0: # 가로일 때
                    h_sum = h_sum * 10 + paper[i][j]
                else: # 세로일 때 초기화
                    sum += h_sum
                    h_sum = 0
            sum += h_sum
        #세로 합
        for j in range(m):
            v_sum = 0
            for i in range(n):
                idx = i * m + j
                if mask & (1 << idx) == 0: # 세로일 때
                    v_sum = v_sum * 10 + paper[i][j]
                else: # 가로 일 때 초기화
                    sum += v_sum
                    v_sum = 0

            sum += v_sum
        ans = max(ans, sum)
    return ans

n, m = map(int, input().split())
paper = [list(map(int, input())) for _ in range(n)]
print(solve())