[백준] 16937번 두 스티커 - Python / 알고리즘 중급 2/3 - 브루트 포스 - 문제

ByungJik_Oh·2025년 7월 16일

[Baekjoon Online Judge]

목록 보기

205/244

💡 문제

크기가 H×W인 모눈종이와 스티커 N개가 있다. i번째 스티커의 크기는 R $_i$ ×C $_i$ 이다. 모눈종이는 크기가 1×1인 칸으로 나누어져 있으며, 간격 1을 두고 선이 그어져 있다.

오늘은 모눈종이에 스티커 2개를 붙이려고 한다. 스티커의 변은 격자의 선과 일치하게 붙여야 하고, 두 스티커가 서로 겹치면 안 된다. 단, 스티커가 접하는 것은 가능하다. 스티커를 90도 회전시키는 것은 가능하다. 스티커가 모눈종이를 벗어나는 것은 불가능하다.

두 스티커가 붙여진 넓이의 최댓값을 구해보자.

입력

첫째 줄에 모눈종이의 크기 H, W, 둘째 줄에 스티커의 수 N이 주어진다. 다음 N개의 줄에는 스티커의 크기 R $_i$ , C $_i$ 가 주어진다.

출력

첫째 줄에 두 스티커가 붙여진 넓이의 최댓값을 출력한다. 두 스티커를 붙일 수 없는 경우에는 0을 출력한다.

제한

1 ≤ H, W, N ≤ 100
1 ≤ R $_i$ , C $_i$ ≤ 100

💭 접근

처음에는 가능한 모든 스티커를 붙여야 하는 줄 알고 문제를 전혀 다른 방향으로 풀었었다...
그러던 중 2개의 스티커만 붙일 수 있다는 것을 보았고 난이도가 확 낮아졌다.

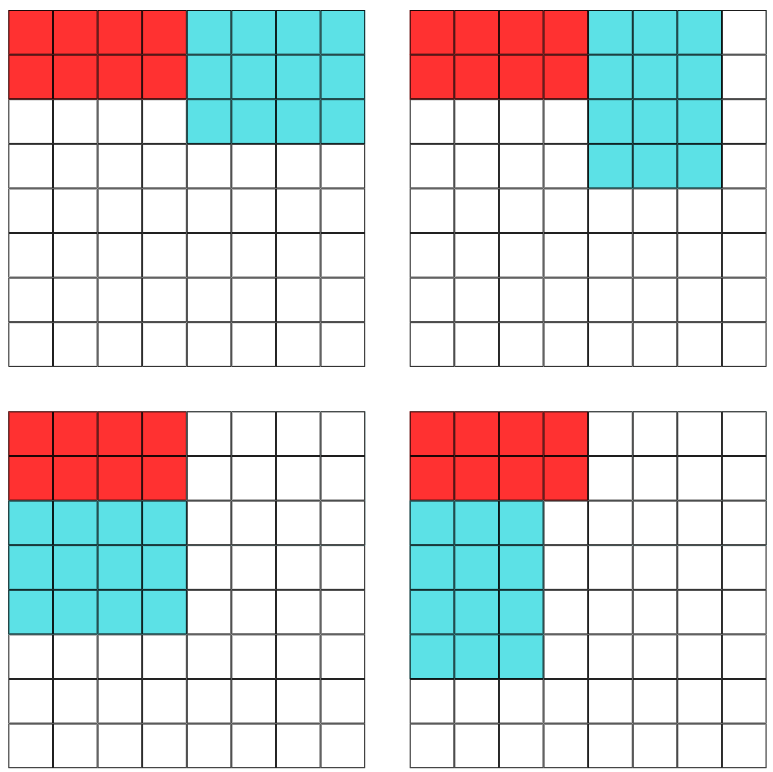
이 문제는 위 그림처럼 간단한 2중 for문으로 두 개의 스티커를 선택한 뒤, 이들을 겹치지 않고 돌리면서 모눈종이에 붙일 수 있는지 판단 후, 두 스티커의 면적을 더해 이들의 최대값을 구하면 되는 문제이다.

다음은 모눈종이에 두 스티커를 붙일 수 있는지 판단하는 함수이다.

def can(r1, c1, r2, c2):
    if (r1 + r2 <= h and max(c1, c2) <= w) or (r1 + r2 <= w and max(c1, c2) <= h):
        return True
    if (r1 + c2 <= h and max(c1, r2) <= w) or (r1 + c2 <= w and max(c1, r2) <= h):
        return True
    if (c1 + r2 <= h and max(r1, c2) <= w) or (c1 + r2 <= w and max(r1, c2) <= h):
        return True
    if (c1 + c2 <= h and max(r1, r2) <= w) or (c1 + c2 <= w and max(r1, r2) <= h):
        return True
    return False

위 함수를 사용하여 붙일 수 있는지 판단하고, 가능하면 넓이를 구해 최대값과 비교하여 정답을 구하면 된다.

📒 코드

def can(r1, c1, r2, c2):
    if (r1 + r2 <= h and max(c1, c2) <= w) or (r1 + r2 <= w and max(c1, c2) <= h):
        return True
    if (r1 + c2 <= h and max(c1, r2) <= w) or (r1 + c2 <= w and max(c1, r2) <= h):
        return True
    if (c1 + r2 <= h and max(r1, c2) <= w) or (c1 + r2 <= w and max(r1, c2) <= h):
        return True
    if (c1 + c2 <= h and max(r1, r2) <= w) or (c1 + c2 <= w and max(r1, r2) <= h):
        return True
    return False

h, w = map(int, input().split())
n = int(input())
sticker = [list(map(int, input().split())) for _ in range(n)]

if n < 2:
    print(0)
else:
    ans = 0
    for i in range(n - 1):
        for j in range(i + 1, n):
            r1, c1 = sticker[i]
            r2, c2 = sticker[j]

            if can(r1, c1, r2, c2):
                ans = max(ans, r1 * c1 + r2 * c2)

    print(ans)