[백준] 1891번 사분면 - Python / 알고리즘 중급 1/3 - 분할 정복 (연습)

ByungJik_Oh·2025년 7월 1일

[Baekjoon Online Judge]

목록 보기

180/244

💡 문제

하나의 좌표평면은 다음과 같이 네 개의 사분면으로 나뉜다.

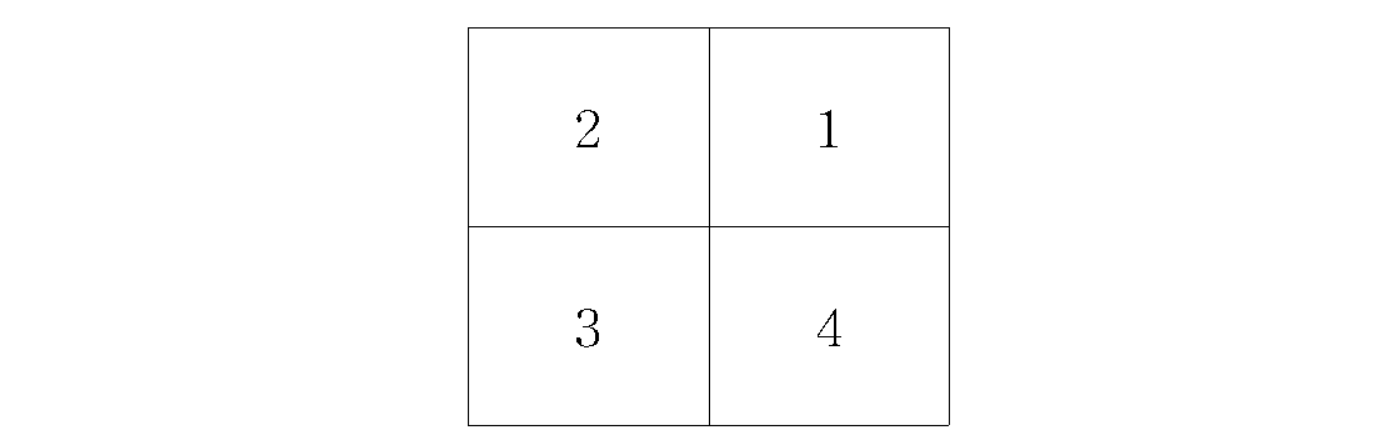
그러면, 각각의 사분면을 다시 사분면으로 나누어 번호를 붙여 보면 어떨까? 예를 들어 1번 사분면의 1번 사분면은 11번 사분면, 3번 사분면의 2번 사분면은 32번 사분면이라고 하면 좋지 않을까? 물론 한 번 더 나눠 볼 수도 있겠다. 3번 사분면의 4번 사분면의 1번 사분면은 341번 사분면이다.

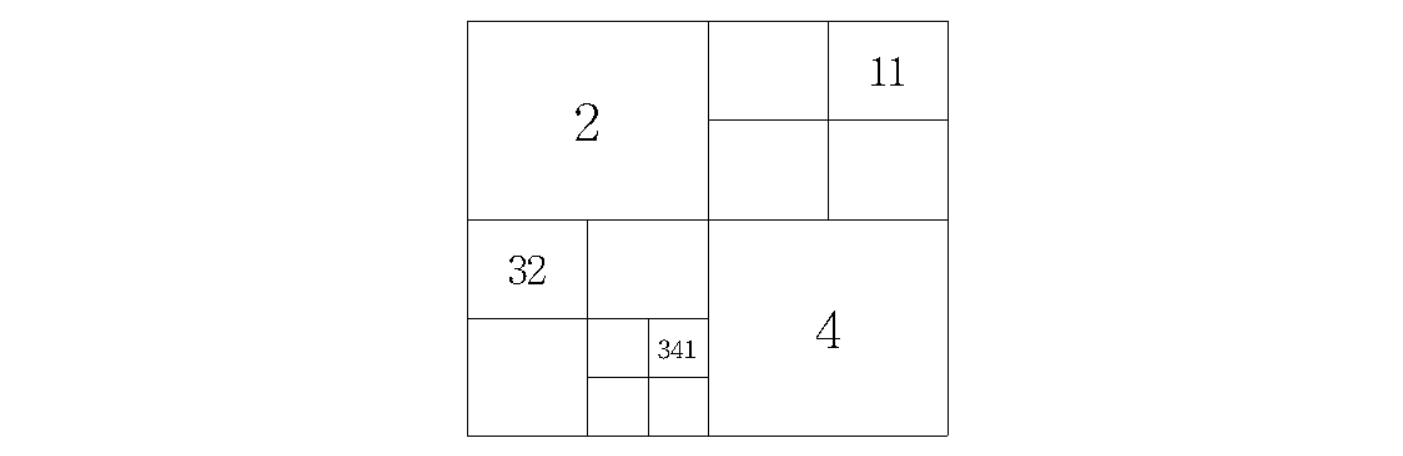
사분면의 번호 길이가 길어짐에 따라 각각의 사분면의 크기는 급격히 작아지며, 그 개수는 기하급수적으로 증가한다.

사분면에 번호를 붙이는 이러한 규칙을 상정하고서, 어떤 사분면 조각을 이동시켰을 때, 그 조각이 위치하게 되는 사분면의 번호가 궁금하다. 예를 들어, 341번 사분면을 오른쪽으로 두 번, 위쪽으로 한 번 이동시키면 424번 사분면에 온다.

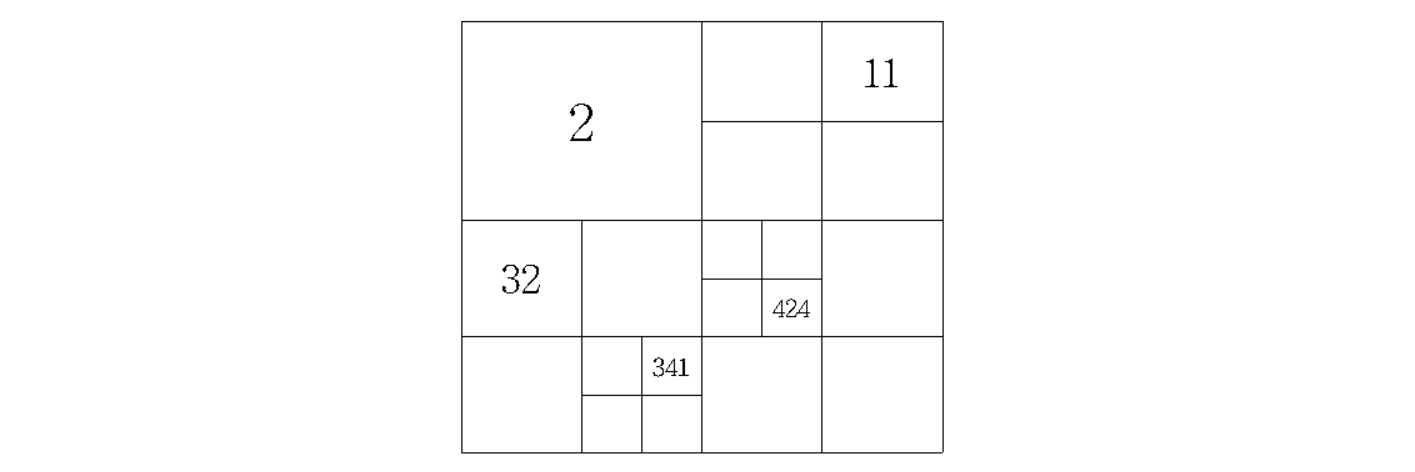
하나의 사분면 조각을 이동시켰을 때, 그 조각이 도착한 사분면의 번호를 알아내는 프로그램을 작성하라.

입력

첫 줄에 이동시키려는 사분면 조각 번호의 자릿수를 나타내는 정수 d와, 그 사분면 조각의 번호가 주어진다. (1 ≤ d ≤ 50) 둘째 줄에는 이동의 내용을 나타내는 두 정수가 x, y가 주어진다. (|x|, |y| ≤ $2^{50}$ ) 오른쪽으로 이동한 경우 x가 양수, 왼쪽으로 이동한 경우 음수이며, 그 절댓값은 오른쪽 왼쪽 방향 이동 횟수를 나타낸다. 위쪽으로 이동한 경우 y가 양수, 아래쪽으로 이동한 경우 음수이며, 역시 그 절댓값은 아래위 방향 이동 횟수를 나타낸다.

출력

첫 줄에 도착한 사분면의 번호를 출력한다. 만약, 존재하지 않는 사분면인 경우에는 -1을 출력한다.

💭 접근

이 문제는 1074번 Z 문제와 굉장히 유사한 문제이다. 이 문제도 마찬가지로 문제 제목에서도 나와있듯이, 사각형 영역을 사분면으로 나누면 규칙을 찾아볼 수 있다. 아래는 d가 3일 때의 그림이다.

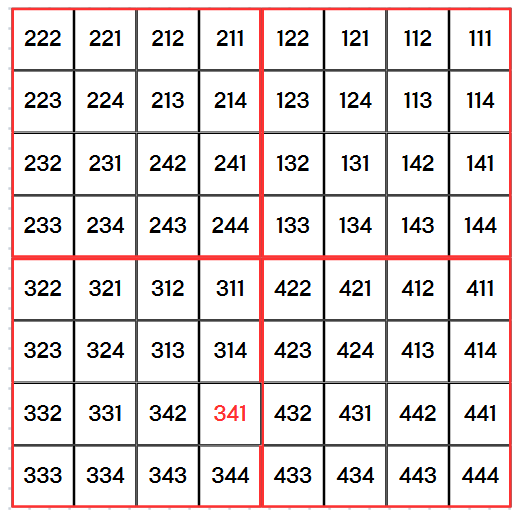
각 네모에 들어있는 숫자를 보면, 앞에서부터 순서대로 각 사각형 영역에서의 사분면 위치에 따라 1, 2, 3, 4가 결정된다. 예제에서 주어진 341을 보면, 현재 사각형 기준으로 사분면을 나누었을 때 3사분면에 위치하기 때문에, 첫번째 숫자가 3이된다.

이제 사각형 영역을 더 줄여보자.

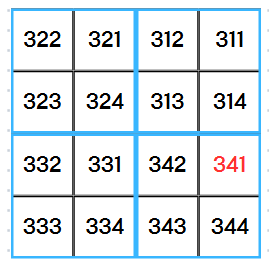
현재 사각형 기준에서는 4사분면에 위치하므로 두번째 숫자는 4가 된다.

마지막으로 사각형 영역을 더 줄여보자.

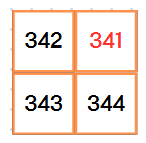
마지막으로 제일 작은 사각형 영역에서는 2사분면에 위치하기 때문에 마지막 숫자는 1이된다.

따라서 기준이 되는 숫자에 따라 우리는 그 숫자가 사각형에서 위치하는 좌표를 알 수 있다.
이 좌표를 구하는 코드는 다음과 같다.

r, c = 0, 0
for i in num:
    n //= 2
    if i == '1':
        c += n
    elif i == '2':
        pass
    elif i == '3':
        r += n
    elif i == '4':
        r += n
        c += n

이렇게 좌표를 구했다면, 입력으로 주어진 x, y 만큼 좌표를 이동시킨다.

r -= y
c += x

이제는 1074번 Z 문제에서 했던 것처럼, 좌표를 사용해서 다시 그 좌표에 있는 숫자값을 구할 차례이다.

이때는 현재 사각형의 좌표가 몇 사분면에 존재하는지 구한 뒤, 그 사분면에 맞는 숫자를 정답에 하나씩 더해주면 된다.

ans = ''
n = 2 ** int(d)
while n > 1:
    if 0 <= r < n//2 and 0 <= c < n//2:
        ans += '2'
    elif 0 <= r < n//2 and n//2 <= c < n:
        ans += '1'
        c -= n//2
    elif n//2 <= r < n and 0 <= c < n//2:
        ans += '3'
        r -= n//2
    elif n//2 <= r < n and n//2 <= c < n:
        ans += '4'
        r -= n//2
        c -= n//2
    else:
        print(-1)
        break
    n //= 2
else:
    print(ans)

이때 한가지 주의해야 할 점으론, 이동시킨 후의 좌표가 사각형의 영역을 벗어난다면 -1을 출력해주어야한다.

📒 코드

d, num = input().split()
x, y = map(int, input().split())
n = 2 ** int(d)

r, c = 0, 0
for i in num:
    n //= 2
    if i == '1':
        c += n
    elif i == '2':
        pass
    elif i == '3':
        r += n
    elif i == '4':
        r += n
        c += n
        
r -= y
c += x

ans = ''
n = 2 ** int(d)
while n > 1:
    if 0 <= r < n//2 and 0 <= c < n//2:
        ans += '2'
    elif 0 <= r < n//2 and n//2 <= c < n:
        ans += '1'
        c -= n//2
    elif n//2 <= r < n and 0 <= c < n//2:
        ans += '3'
        r -= n//2
    elif n//2 <= r < n and n//2 <= c < n:
        ans += '4'
        r -= n//2
        c -= n//2
    else:
        print(-1)
        break
    n //= 2
else:
    print(ans)