


💡 문제

대략 위의 그림과 같이 생긴 성곽이 있다. 굵은 선은 벽을 나타내고, 점선은 벽이 없어서 지나다닐 수 있는 통로를 나타낸다. 이러한 형태의 성의 지도를 입력받아서 다음을 계산하는 프로그램을 작성하시오.
- 이 성에 있는 방의 개수
- 가장 넓은 방의 넓이
- 하나의 벽을 제거하여 얻을 수 있는 가장 넓은 방의 크기
위의 예에서는 방은 5개고, 가장 큰 방은 9개의 칸으로 이루어져 있으며, 위의 그림에서 화살표가 가리키는 벽을 제거하면 16인 크기의 방을 얻을 수 있다.
성은 M × N(1 ≤ M, N ≤ 50)개의 정사각형 칸으로 이루어진다. 성에는 최소 두 개의 방이 있어서, 항상 하나의 벽을 제거하여 두 방을 합치는 경우가 있다.
입력
첫째 줄에 두 정수 N, M이 주어진다. 다음 M개의 줄에는 N개의 정수로 벽에 대한 정보가 주어진다. 벽에 대한 정보는 한 정수로 주어지는데, 서쪽에 벽이 있을 때는 1을, 북쪽에 벽이 있을 때는 2를, 동쪽에 벽이 있을 때는 4를, 남쪽에 벽이 있을 때는 8을 더한 값이 주어진다. 참고로 이진수의 각 비트를 생각하면 쉽다. 따라서 이 값은 0부터 15까지의 범위 안에 있다.
출력
첫째 줄에 1의 답을, 둘째 줄에 2의 답을, 셋째 줄에 3의 답을 출력한다.
💭 접근
이 문제는 입력으로 주어진 숫자들을 이진화하여 벽의 유무를 파악한 뒤 탐색을 이어나가는 문제이다.
사실 이 부분만 해결된다면 나머지는 이제까지 많이 만나왔던 문제 유형이다.
하나씩 차근차근 살펴보자.
- 우선 서로 구별되어 있는 방의 개수를 구해야 하므로 각 칸에 존재하는 숫자를 이진화하여 각 방들을 그룹화한다.
# 서 북 동 남
dx = [0, -1, 0, 1]
dy = [-1, 0, 1, 0]
group_num = 0
for x in range(m):
for y in range(n):
if grouped[x][y] == -1:
size = 1
bfs(x, y)
group_num += 1
group_size.append(size)def bfs(x, y):
global size
q = deque()
q.append([x, y])
grouped[x][y] = group_num
while q:
x, y = q.popleft()
curr = graph[x][y]
for i in range(3, -1, -1): # 남 동 북 서
if curr >= 2**i:
curr -= 2**i
else:
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < m and 0 <= ny < n and grouped[nx][ny] == -1:
grouped[nx][ny] = group_num
size += 1
q.append([nx, ny])이때 코드를 잘보면 각 방을 그룹화하면서 각 방의 크기까지 동시에 저장해야 불필요한 계산을 방지할 수 있다.
각 방의 숫자를 통해 벽을 찾고, 탐색하는 코드를 살펴보자
curr = graph[x][y]
for i in range(3, -1, -1): # 남 동 북 서
if curr >= 2**i:
curr -= 2**i
else:
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < m and 0 <= ny < n and grouped[nx][ny] == -1:
grouped[nx][ny] = group_num
size += 1
q.append([nx, ny])위 코드가 핵심인데, 각 칸에 적혀있는 숫자를 8, 4, 2, 1 순으로 비교하며 크다면 벽이 존재하는 것이므로 탐색X, 만약 작다면 벽이 존재하지 않는 것이므로 탐색을 진행한다.
예를 들어 임의의 한 칸에 11이라는 숫자가 적혀있다고 가정해보자.
ex.
curr = 11
i = 3-> 11은 8보다 크므로 벽 존재 남쪽 방향 벽 존재, 11에서 8을 뺀다.
i = 2-> 3은 4보다 작으므로 벽 존재 X 동쪽 방향 벽 없음, 탐색 진행
i = 1-> 3은 2보다 크므로 벽 존재 북쪽 방향 벽 존재, 3에서 2를 뺀다.
i = 0-> 1은 0보다 크므로 벽 존재 서쪽 방향 벽 존재
따라서 11은 (1011) 이므로 동쪽 방향에서만 탐색을 진행한다.
위 과정을 거치면 예제를 예시로 들었을 때 아래 그림과 같이 저장된다.
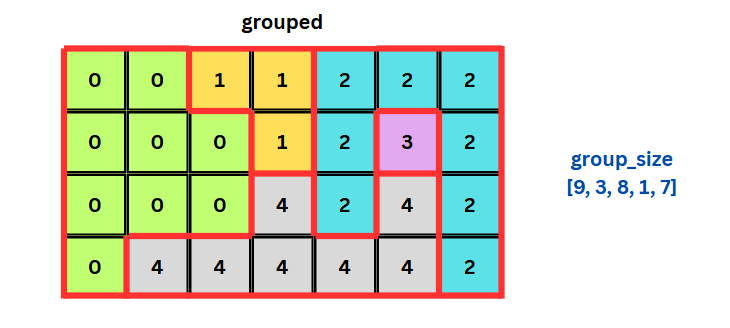
- 이제 마지막으로 인접한 서로 다른 두 그룹의 크기를 더하여 벽을 하나 허물었을 때 구할 수 있는 가장 큰 그룹의 크기를 구하면 된다.
merged_size = 0
for x in range(m):
for y in range(n):
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < m and 0 <= ny < n and grouped[x][y] != grouped[nx][ny]:
merged_size = max(merged_size,
group_size[grouped[x][y]] + group_size[grouped[nx][ny]])📒 코드
from collections import deque
def bfs(x, y):
global size
q = deque()
q.append([x, y])
grouped[x][y] = group_num
while q:
x, y = q.popleft()
curr = graph[x][y]
for i in range(3, -1, -1): # 남 동 북 서
if curr >= 2**i:
curr -= 2**i
else:
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < m and 0 <= ny < n and grouped[nx][ny] == -1:
grouped[nx][ny] = group_num
size += 1
q.append([nx, ny])
n, m = map(int, input().split())
graph = [list(map(int, input().split())) for _ in range(m)]
grouped = [[-1 for _ in range(n)] for _ in range(m)]
group_size = []
# 서 북 동 남
dx = [0, -1, 0, 1]
dy = [-1, 0, 1, 0]
group_num = 0
for x in range(m):
for y in range(n):
if grouped[x][y] == -1:
size = 1
bfs(x, y)
group_num += 1
group_size.append(size)
merged_size = 0
for x in range(m):
for y in range(n):
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < m and 0 <= ny < n and grouped[x][y] != grouped[nx][ny]:
merged_size = max(merged_size,
group_size[grouped[x][y]] + group_size[grouped[nx][ny]])
print(len(group_size))
print(max(group_size))
print(merged_size)💭 후기
벽의 존재 유뮤를 숫자로 나타내어 재밌었던 문제였다.
🔗 문제 출처
https://www.acmicpc.net/problem/2234
