


💡 문제
n개의 정점을 갖는 이진 트리의 정점에 1부터 n까지의 번호가 중복 없이 매겨져 있다. 이와 같은 이진 트리의 인오더와 포스트오더가 주어졌을 때, 프리오더를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 n(1 ≤ n ≤ 100,000)이 주어진다. 다음 줄에는 인오더를 나타내는 n개의 자연수가 주어지고, 그 다음 줄에는 같은 식으로 포스트오더가 주어진다.
출력
첫째 줄에 프리오더를 출력한다.
💭 접근
우선 이 문제를 해결하기 위해 트리의 전위, 중위, 후위 순회에 대해 알 필요가 있다.
전위 순회: root -> left -> right
중위 순회: left -> root -> right
후위 순회: left -> right -> root
풀이를 쉽게 이해하기 위해 아래와 같은 트리와 함께 보자.
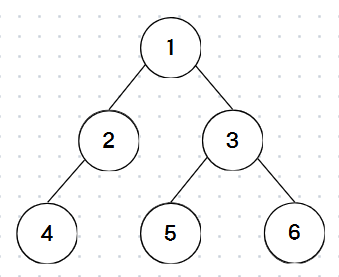
위 트리의 전위, 중위, 후위 순회를 구하면 다음과 같다.
전위 순회: 1 2 4 3 5 6
중위 순회: 4 2 1 5 3 6
후위 순회: 4 2 5 6 3 1
이제 문제와 같이 중위, 후위 순회의 특징을 활용하여 전위 순회를 구해보자.
먼저 주목할 것은 후위 순회의 마지막 원소는 반드시 루트 노드라는 것이다.
따라서 루트 노드가 우선 순위가 가장 높은 전위 순회의 특성 상, 재귀를 진행하면서 후위 순회의 마지막 원소를 출력해준다.
이후, 루트 노드의 왼쪽 트리, 오른쪽 트리를 구분해서 각각의 트리에서도 재귀를 사용해 루트 노드를 찾아서 출력해주면된다.
그렇다면 어떻게 루트 노드의 왼쪽 트리, 오른쪽 트리를 구분할 수 있을까?
이때 중위 순회를 보면, 직전의 후위 순회의 마지막 원소(루트) 1을 기준으로 왼쪽에 있는 노드들은 왼쪽 트리의 노드, 오른쪽에 있는 노드들은 오른쪽 트리의 노드라는 것을 눈치챌 수 있다.
아래 그림과 함께 보자.
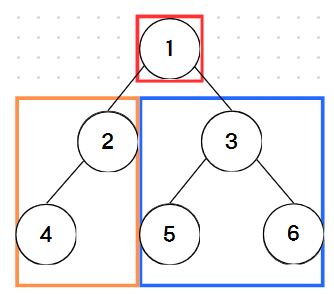
중위 순회: 4 2 1 5 3 6
후위 순회: 4 2 5 6 3 1
또한 후위 순회도 마찬가지로 규칙을 찾을 수 있다.
이제 재귀를 호출할 때 어떻게 호출해야 할지 위 규칙을 활용해서 구현해보자.
먼저 전위 순회는 루트 노드를 출력한 뒤, 왼쪽 트리에 대해서 모두 출력한 뒤, 오른쪽 트리에 대해서 출력해야 한다.
따라서 왼쪽 트리를 먼저 호출해야 하는데, 우선 코드로 보면 다음과 같다.
pre_order(in_left, root_idx - 1, post_left, post_left + tmp - 1)위에서 볼수 있듯이 중위 순회에서 왼쪽 트리의 범위는 루트 노드를 중심으로 나뉘기 때문에 중위 순회에서 왼쪽 트리의 범위는 중위 순회의 시작부터 루트 노드의 인덱스 - 1이다.
또한 후위 순회에서는 가장 앞의 노드부터 중위 순회에서의 루트 노드의 인덱스 - 1까지이다.
이후 오른쪽 트리를 호출할 때에는, 다음과 같다.
pre_order(root_idx + 1, in_right, post_left + tmp, post_right - 1)마찬가지로 중위 순회에서 오른쪽 트리의 범위는 루트 노드를 중심으로 루트 노드의 인덱스 + 1부터 중위 순회의 끝까지이다.
마지막으로 후위 순회에서는 앞서 사용했던 후위 순회 기준 왼쪽 트리의 끝 값 + 1부터 루트 노드의 바로 직전 노드까지이다.
이때 위 방법에서 알 수 있듯이 중위 순회에서 루트 노드의 인덱스를 계속해서 찾아야 하므로 index() 함수를 사용할 시 시간초과가 발생할 수 있다.
따라서 재귀 함수를 호출하기 전, 딕셔너리를 사용하여 각 노드의 중위 순회에서의 인덱스를 저장해놓으면 O(1)의 시간복잡도로 인덱스를 찾을 수 있다.
📒 코드
import sys
sys.setrecursionlimit(10**6)
def pre_order(in_left, in_right, post_left, post_right):
if in_left > in_right: return
# 로트 노드는 후위순회의 마지막 원소
root = post_order[post_right]
# 중위 순회는 루트 노드 우선 출력
print(root, end=' ')
root_idx = idx[root]
tmp = root_idx - in_left
# 왼쪽 노드 탐색
pre_order(in_left, root_idx - 1, post_left, post_left + tmp - 1)
# 오른쪽 노드 탐색
pre_order(root_idx + 1, in_right, post_left + tmp, post_right - 1)
n = int(input())
in_order = list(map(int, input().split()))
post_order = list(map(int, input().split()))
idx = {value: index for index, value in enumerate(in_order)}
pre_order(0, n - 1, 0, n - 1)💭 후기
머리로는 이해했지만 글로 풀려니 쉽지 않은 문제... 계속 다시 읽어보고 수정해야겠다.
🔗 문제 출처
https://www.acmicpc.net/problem/2263
