💡 문제
상근이는 감옥에서 죄수 두 명을 탈옥시켜야 한다. 이 감옥은 1층짜리 건물이고, 상근이는 방금 평면도를 얻었다.
평면도에는 모든 벽과 문이 나타나있고, 탈옥시켜야 하는 죄수의 위치도 나타나 있다. 감옥은 무인 감옥으로 죄수 두 명이 감옥에 있는 유일한 사람이다.
문은 중앙 제어실에서만 열 수 있다. 상근이는 특별한 기술을 이용해 제어실을 통하지 않고 문을 열려고 한다. 하지만, 문을 열려면 시간이 매우 많이 걸린다. 두 죄수를 탈옥시키기 위해서 열어야 하는 문의 개수를 구하는 프로그램을 작성하시오. 문을 한 번 열면 계속 열린 상태로 있는다.
입력
첫째 줄에 테스트 케이스의 개수가 주어진다. 테스트 케이스의 수는 100개를 넘지 않는다.
첫째 줄에는 평면도의 높이 h와 너비 w가 주어진다. (2 ≤ h, w ≤ 100) 다음 h개 줄에는 감옥의 평면도 정보가 주어지며, 빈 공간은 '.', 지나갈 수 없는 벽은 '*', 문은 '#', 죄수의 위치는 '$'이다.
상근이는 감옥 밖을 자유롭게 이동할 수 있고, 평면도에 표시된 죄수의 수는 항상 두 명이다. 각 죄수와 감옥의 바깥을 연결하는 경로가 항상 존재하는 경우만 입력으로 주어진다.
출력
각 테스트 케이스마다 두 죄수를 탈옥시키기 위해서 열어야 하는 문의 최솟값을 출력한다.
💭 접근
이 문제를 해결하기 위해 가장 핵심적인 아이디어로는
먼저 입력으로 들어온 감옥의 평면도에 겉부분에 빈 공간을 만들어주고(Padding),
모든 각각의 칸에 대해 죄수 1이 모든 공간을 방문하기 위해 연 문의 최소 개수를 저장한 List와
모든 각각의 칸에 대해 죄수 2가 모든 공간을 방문하기 위해 연 문의 최소 개수를 저장한 List,
마지막으론 모든 각각의 칸에 대해 감옥 외부에서 들어온 사람(Padding으로 추가한 곳에서 출발한 사람)이 모든 공간을 방문하기 위해 연 문의 최소 개수를 저장한 List까지 총 3개의 List를 생성한 다음,
이 셋이 만나는 한 지점에 대해 각 사람이 연 문의 개수를 더하여 최소값을 구해주면 된다.
아래 그림을 보며 이해해보자. (예제 1의 첫번째 입력의 예시이다.)
****#****
*..#.#..*
****.****
*$#.#.#$*
*********1. 먼저 주어진 공간에 외부 공간(Padding)을 추가한다.
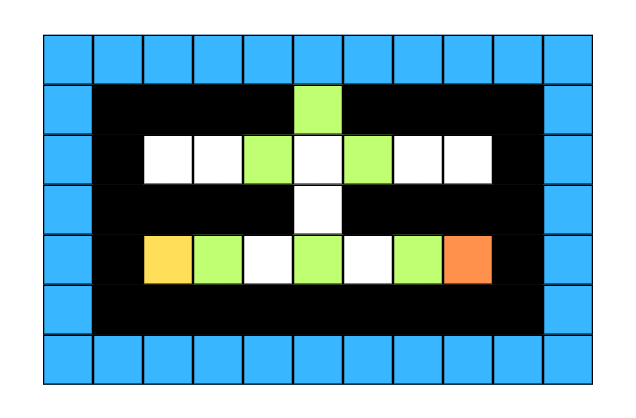
검정색 공간은 벽, 초록색 공간은 문, 파란색 공간은 추가한 외부 공간(Padding), 노란색은 죄수 1, 주황색은 죄수 2의 위치를 나타낸다.
이를 코드로 나타내면 다음과 같다.
graph = [['.' for _ in range(w + 2)]]
for i in range(h):
graph.append(list('.' + input().strip() + '.'))
graph.append(['.' for _ in range(w + 2)])2. 이제 죄수 1, 죄수 2, 그리고 외부 공간에서 들어오는 사람에 대한 각 칸에 도달하기 위해 열어야 하는 문의 최소 개수를 구한다.
pri1 = bfs(pos[0][0], pos[0][1])
pri2 = bfs(pos[1][0], pos[1][1])
s = bfs(0, 0)이때 열어야 하는 문의 최소 개수를 구해야하므로 문을 열지 않아도 되는 칸을 우선적으로 탐색해야한다.
이는 0-1 BFS를 통해 문을 열지 않아도 되는 칸에 우선순위를 두어 먼전 탐색할 수 있도록 한다.
def bfs(x, y):
visited = [[-1 for _ in range(w + 2)] for _ in range(h + 2)]
q = deque()
q.append([x, y])
visited[x][y] = 0
while q:
x, y = q.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < h + 2 and 0 <= ny < w + 2:
if visited[nx][ny] == -1:
if graph[nx][ny] == '.' or graph[nx][ny] == '$':
visited[nx][ny] = visited[x][y]
q.appendleft([nx, ny])
elif graph[nx][ny] == '#':
visited[nx][ny] = visited[x][y] + 1
q.append([nx, ny])
return visited이렇게 탐색을 마치면 각각의 List에는 다음과 같이 저장된다. 각 칸의 숫자는 각 칸을 방문하기 위해 열어야 하는 문의 최소 개수이다.
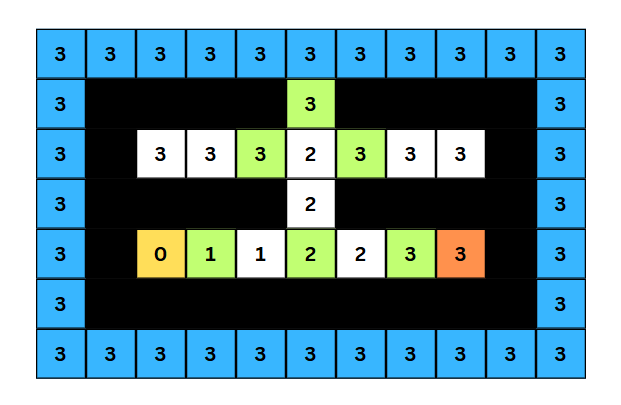
- 죄수 1
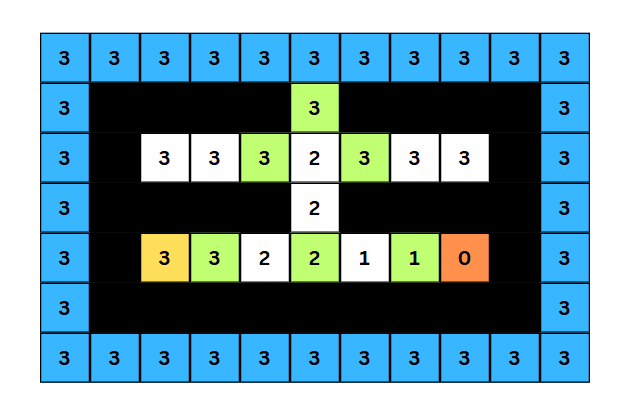
- 죄수 2
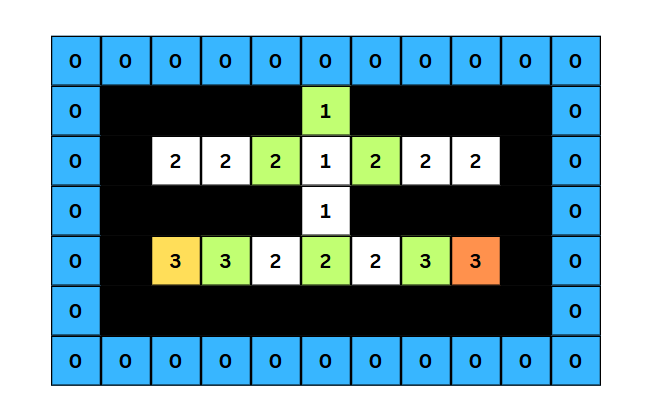
- 외부인
- 이제 마지막으로 각 칸을 순회하며 해당 칸에서 이 세 사람이 만났다고 가정했을 때, 세사람이 열어야하는 문의 개수의 합 중 최소를 구해주면 된다.
ans = float('inf')
for i in range(h + 2):
for j in range(w + 2):
if pri1[i][j] != -1 and pri2[i][j] != -1 and s[i][j] != -1:
tmp_ans = pri1[i][j] + pri2[i][j] + s[i][j]
if graph[i][j] == '*':
continue
if graph[i][j] == '#':
tmp_ans -= 2
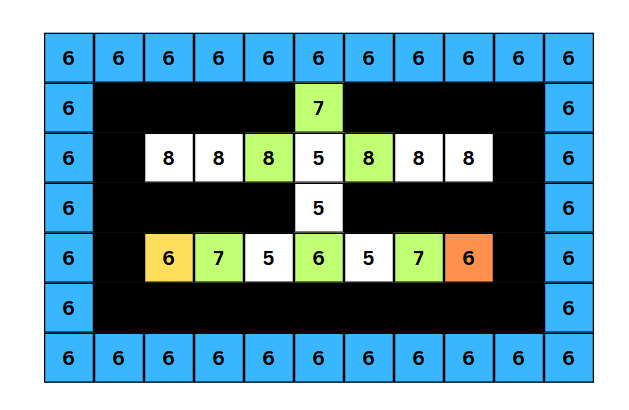
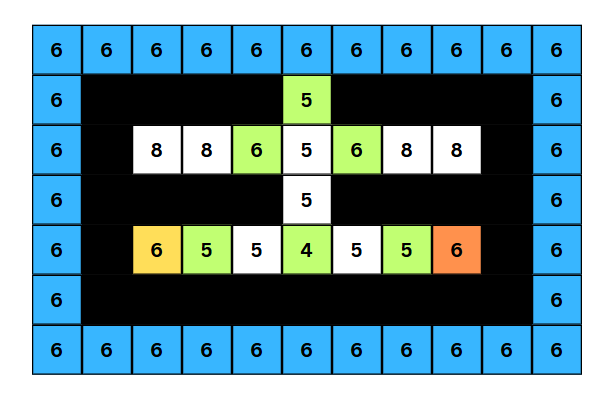
ans = min(ans, tmp_ans)코드에서는 한 칸씩 비교하지만, 이해를 쉽게 하기 위해 위 세 그림을 더한 그림을 그리면 다음과 같다.
- 세 사람이 한 지점에서 만나기 위해 열어야 하는 각 칸의 최소 문의 개수
이렇게 그림을 보게 되면 모든 칸중 가장 작은 수를 가지는 5가 정답이 된다고 볼수 있다.
그러나 이 문제에서 한가지 유의해야 할 점이 있는데, 문제에서 주어진 바와 같이
"문을 한 번 열면 계속 열린 상태로 있는다." 라는 것이다.
따라서 위 그림은 정확하지 않으며, 만약 세 사람이 초록색 칸(문)에서 만난다고 가정하면 세 명이서 똑같은 문을 3번 연 것이 되므로 이는 정확하지 않다.
그러므로 세 사람이 문에서 만날 경우 한 사람만 문을 열면 나머지 두 사람도 통과 가능하므로, 문이 있는 칸에 대해서는 -2를 해주어야 한다.
- 수정된 그림
따라서 4가 정답이 된다.
물론 위 그림도 정확한 문의 개수를 구한 것은 아니지만, 문을 열어야만 갈 수 있는 칸들은 문이 존재하는 칸보다 숫자가 크거나 같을 수 밖에 없기 때문에 문이 있는 칸에 대해서만 개수를 고려해도 정답을 도출해 낼 수 있다.
📒 코드
from collections import deque
def bfs(x, y):
visited = [[-1 for _ in range(w + 2)] for _ in range(h + 2)]
q = deque()
q.append([x, y])
visited[x][y] = 0
while q:
x, y = q.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < h + 2 and 0 <= ny < w + 2:
if visited[nx][ny] == -1:
if graph[nx][ny] == '.' or graph[nx][ny] == '$':
visited[nx][ny] = visited[x][y]
q.appendleft([nx, ny])
elif graph[nx][ny] == '#':
visited[nx][ny] = visited[x][y] + 1
q.append([nx, ny])
return visited
t = int(input())
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
for _ in range(t):
h, w = map(int, input().split())
graph = [['.' for _ in range(w + 2)]]
for i in range(h):
graph.append(list('.' + input().strip() + '.'))
graph.append(['.' for _ in range(w + 2)])
pos = []
for i in range(h + 2):
for j in range(w + 2):
if graph[i][j] == '$':
pos.append([i, j])
pri1 = bfs(pos[0][0], pos[0][1])
pri2 = bfs(pos[1][0], pos[1][1])
s = bfs(0, 0)
ans = float('inf')
for i in range(h + 2):
for j in range(w + 2):
if pri1[i][j] != -1 and pri2[i][j] != -1 and s[i][j] != -1:
tmp_ans = pri1[i][j] + pri2[i][j] + s[i][j]
if graph[i][j] == '*':
continue
if graph[i][j] == '#':
tmp_ans -= 2
ans = min(ans, tmp_ans)
print(ans)💭 후기
죄수가 감옥을 나간다고만 생각했지 외부인을 추가하여 세 사람이 만나는 지점의 최솟값을 구해야 한다는 생각을 떠올리기가 쉽지 않았다.
🔗 문제 출처
https://www.acmicpc.net/problem/9376