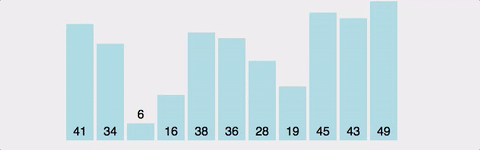
비교방식 알고리즘
- 버블 정렬(Bubble Sort)
- 선택 정렬(Selection Sort)
- 삽입 정렬(Insertion Sort)
- 합병 정렬(Merge Sort)
- 힙 정렬(Heap Sort)
- 퀵 정렬(Quick Sort)
버블 정렬
size가 n인 배열을 정렬 할때, i를 0부터 n-1까지 1씩 증가시키며 i와 i+1인 원소와 비교하여 arr[i] > arr[i+1]인 경우 두 원소를 swap해가며 정렬한다. n개의 크기의 배열을 순회하며 한번의 수행마다 마다 n-1번 비교를 수행하기 때문에 의 시간 복잡도를 갖는다.
-
장점
- 구현이 간단하다
-
단점
- 불필요한 교환이 많이 일어난다.
효율이 좋지 않아 거의 사용되지 않는다
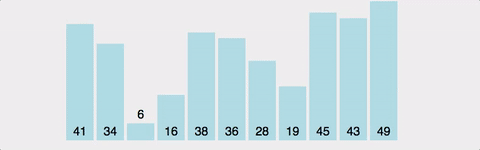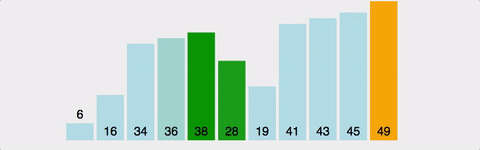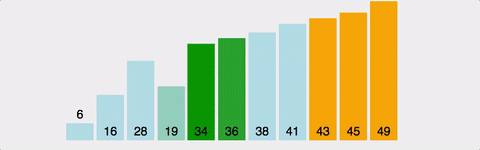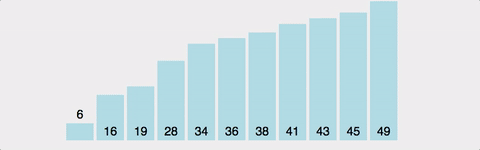
버블 정렬 예시
| Space Complexity | Time Complexity |
|---|---|
선택 정렬
size가 n인 배열을 정렬 할 때, i를 0부터 n-1까지 1씩 증가시키며 i ~ n 까지의 원소 중 최소값의 위치를 확인한 후 최소값과 i번째 원소를 swap해가며 정렬한다.

선택 정렬 예시
| Space Complexity | Time Complexity |
|---|---|
삽입 정렬
인덱스 i로 배열을 순회하며 arr[i]를 arr[0:i]와 비교하며 arr[i]보다 작은 값 앞에 삽입한다. 이 때 arr[0:i]는 정렬되어 있다고 가정한다.
n개의 원소를 가진 배열을 정렬할 때, i를 1부터 n-1까지 1씩 증가시킨다. 이 때 0부터 i-1까지의 원소는 정렬 되어 있다는 가정하에, i번째 원소를 i-1부터 0번째 원소까지 비교하면서 i번째 원소가 비교하는 원소보다 작을 경우, 비교하는 원소를 오른쪽으로 한칸 옮긴다. 비교하는 원소의 인덱스를 aux라고 할 때 aux-- 위치의 원소와 계속하여 비교해 나가며 arr[aux] < arr[i]일 때 까지 위 시행을 계속한다. arr[aux] < arr[i]인 경우 arr[aux]에 arr[i]의 값을 대입한다.
- 장점
- 알고리즘이 간단하므로 데이터가 적거나, 대부분의 데이터가 정렬되어 있는경우 다른 정렬 알고리즘보다 효율적일 수 있다.
- 단점
- 데이터가 많을 수록 불필요한 이동이 많아진다.

삽입 정렬 예시
| Space Complexity | Time Complexity |
|---|---|
합병 정렬
분할 정복 기법을 사용한다. n개의 원소를 더 이상 나누어지지 않을 때(크기가 1인 배열이 되는 경우)까지 반으로 분할한다. 이후 2개의 배열끼리 병합을 하며 정렬을 수행한다. 이 과정에서 병합된 결과는 임시 배열에 저장되는데 그 크기는 당연히 2배가 된다. 합쳐지는 두 배열은 값이 정렬되어있다고 가정하고 가장 작은 값끼리 하나씩 비교하며 임시 배열에 차례로 넣는다. 이 과정에서 합병된 배열의 크기는 2배씩 커지며 결과적으로는 n의 크기로 돌아온다.
문제를 작은 문제로 분할하여 풀기 때문에 의 시간 복잡도를 갖는다.
- 장점
- 데이터 분포에 영향을 덜 받는다.
- 단점
- 임시배열이 추가로 필요하다.
- 데이터가 많아질 수록 이동 횟수가 많아져 매우 큰 시간적 낭비를 초래한다.
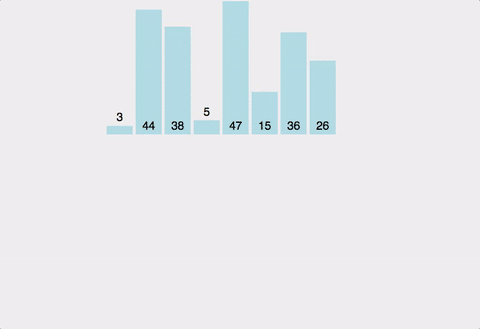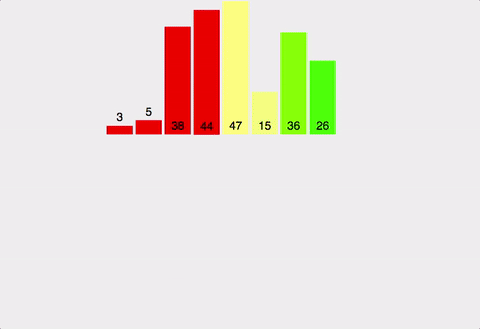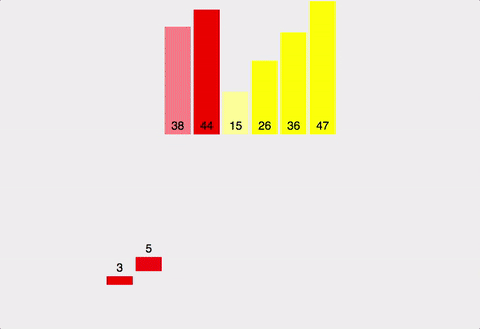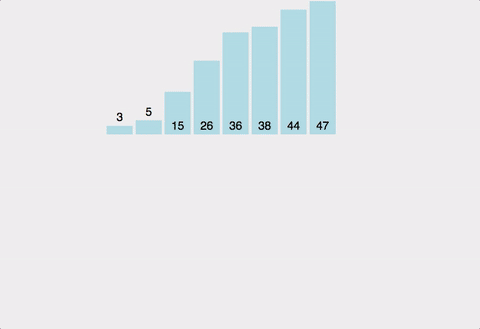
합병 정렬 예시
| Space Complexity | Time Complexity |
|---|---|
힙 정렬
binary heap 자료구조를 사용한다. Heap 구조에서 루트 노드의 값을 하나씩 꺼내며 정렬하는 방식이다. Heap에 데이터를 삽입하고 삭제하는 복잡도는 인데 이 때, 정렬을 하려는 대상이 개이기 때문에 결과적으로 의 시간 복잡도를 갖는다.
- 장점
- 시간 복잡도가 좋은편
- 가장 큰 값 몇개를 필요로할 때 효율적이다.
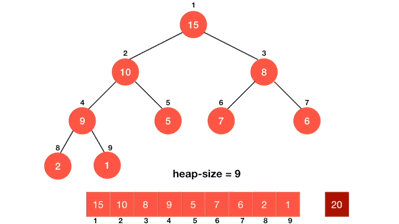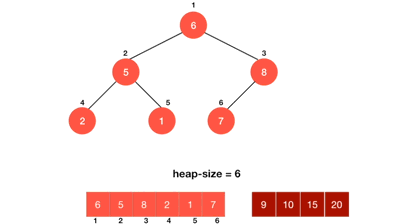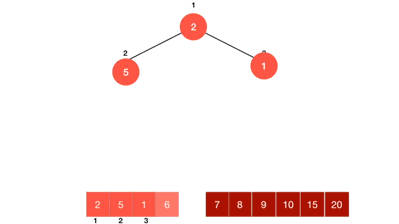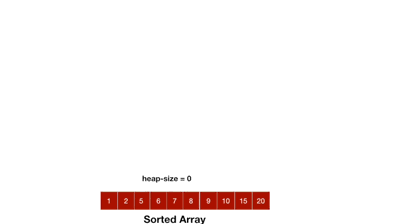
힙 정렬 예시
| Space Complexity | Time Complexity |
|---|---|
퀵 정렬
sorting 기법 중 가장 빠르다고 하여 퀵 정렬이라는 이름이 붙었다. 하지만 최악의 경우 시간복잡도가 가 나올 수도 있다.
퀵 정렬 또한 분할 정복 기법을 사용한다. 분할하는 과정에서 pivot이라는 개념이 사용된다. 입력된 배열에 대해 오름차순으로 정렬한다고 하면 pivot을 기준으로 왼쪽에는 pivot보다 작은 값, 오른쪽에는 pivot보다 큰 값이 위치하도록 partition시킨다. (partition과정은 아래에서 설명하려고 한다.) 이렇게 나뉜 좌, 우측의 배열을 다시 재귀적으로 퀵 정렬을 시킨다.
이 과정을 나뉜 배열의 크키가 1일 때까지 수행을 함으로써 정렬을 시킨다. 이 때 주의할 점은 pivot으로 설정된 값은 다음 재취과정에 포함해야하지 않는다는 것이다. 이미 partition 과정에서 정렬된 자신의 위치를 찾았기 때문이다.
분할 정복 기법을 사용하기 때문에 평균적인 경우 의 시간 복잡도를 갖는다.
- 장점
- 불필요한 이동이 없어 의 시간 복잡도를 갖는 정렬 알고리즘 중에서 일반적으로 가장 빠르다.
- 단점
- 정렬된 배열에 대해 오히려 시간이 오래 걸린다.
partitioning
일단 임의의 pivot을 선택한다. arr[0]를 pivot으로 선택했을 때(pivot = 0), 인덱스 i는 0부터 1씩 증가하며 pivot값보다 큰 값을 찾고, 인덱스 j는 n-1부터 1씩 감소하며 pivot보다 작은 값을 탐색 한다고 하자.
두 인덱스는 각자 조건을 만족하는 값을 찾으면 증감을 멈추고 대기한다. 두 인덱스가 둘 다 각자 pivot 값보다 큰 값, 작은 값을 찾은 경우 두 원소의 값을 swap한다. 그 후 다시 i는 오른쪽(증가), j는 왼쪽(감소)로 이동하며 위 수행을 계속한다. 그러던 중 j <= i 가 되는, 즉, 두 인덱스가 엇갈리게 되거나 같게 되는 순간 위 수행을 중단하고 arr[j]와 arr[pivot]을 swap한다. 이렇게 되면 이전 수행에서 i가 지나간 원소 중 arr[pivot] 보다 큰 값은 j가 지나간 원소 중 arr[pivot]보다 작은 값과 swap해주었기 때문에 pivot을 중심으로 왼쪽에는 arr[pivot]보다 작은 값, 오른쪽에는 pivot보다 큰 값이 위치하게 된다.
위 과정에서 pivot은 본인의 위치가 결정되었기 때문에 배열을 분할하여 arr[0:pivot], arr[pivot+1:n]에 대해 배열의 크기가 1이 될 때까지 재귀적으로 partioning을 수행하면 최종적으로 배열의 모든 원소가 정렬된다.
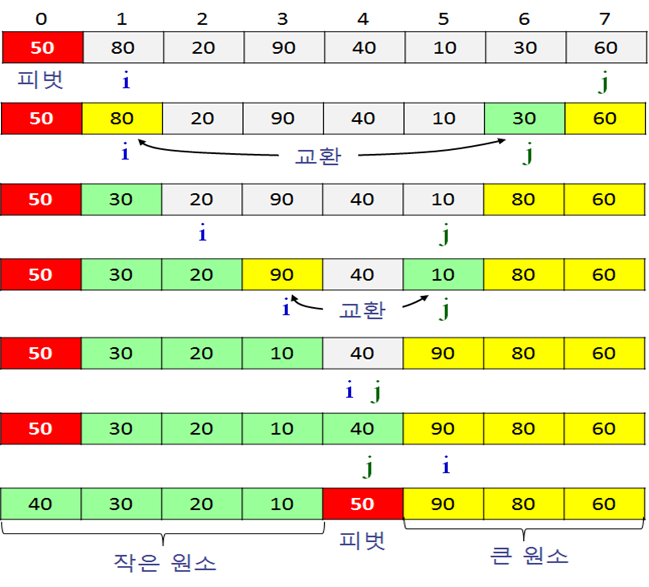
partitioning 정렬 예시
Worst Case
정렬하려는 배열이 이미 오름차순 혹은 내림차순으로 정렬된 경우 pivot 값이 항상 배열에서 가장 큰 값 혹은 작은 값을 갖기 때문에 partition의 크기가 항상 1과 n-1이 된다. 이 경우 크기가 큰 쪽 배열은 계속 n-1, n-2, n-3, ...의 비교 횟수를 갖게 되기 때문에 결과적으로 시간 복잡도 가 된다. 이를 방지하기 위해 random으로 pivot을 정하여 설정하면 입력과 관계 없이 일정한 수준의 성능을 유지할 수 있다.
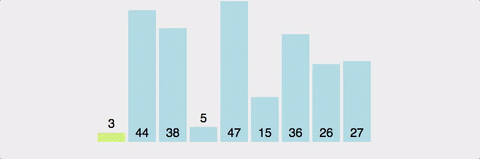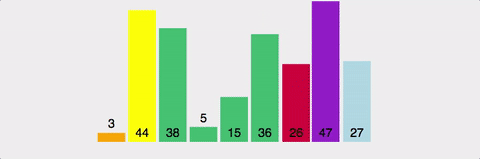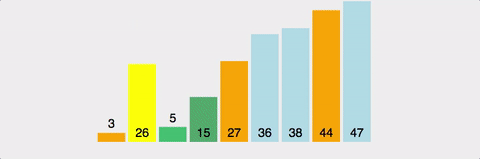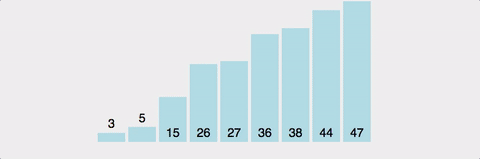
퀵 정렬 예시
| Space Complexity | Time Complexity |
|---|---|