[자료구조] 그래프

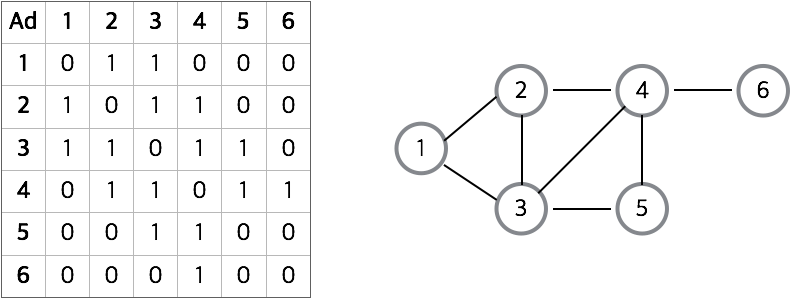
그래프

 정점과 간선의 집합, 트리 또한 그래프이다(사이클은 없다).

그래프를 구현하는 두 방법

인접행렬

  각 vertax간의 연결관계를 $O(1)$로 확인할 수 있다. Dense Graph에 적합하며 항상 $v^2$의 공간 복잡도를 갖는다.

인접리스트

  각 정점에 연결된 정점을 연결리스트에 저장하는 방식이다. 링크드 리스트이기 때문에 탐색이 오래걸린다. 공간복잡도는 $O(V + E)$이다. Sparse Graph를 표현하는데 적합하다.

그래프 탐색

깊이 우선 탐색(Depth First Search, DFS)

 각 정점들과 인접한 정점들을 우선적으로 탐색한다. 한 정점에서 시작하여 도달할 수 있는 마지막 정점까지 탐색한 후 다시 돌아와 다른 인접한 정점를 탐색한다(이 과정을 Back tracking이라고 한다). Stack을 사용하여 구현한다. 탐색한 정점를 Stack에 저장하며 탐색을 하고, 마지막 정점를 탐색한 경우에 아직 탐색하지 않은 인접한 정점이 있는 가장 최근에 탐색한 정점까지 pop하여 되돌아간 후 탐색하지 않은 인접한 노드에서부터 다시 탐색을 시작한다. $O(V + E)$의 시간 복잡도를 갖는다.

너비 우선 탐색(Breadth First Search, BFS)

 Queue를 사용하여 구현한다. 탐색을 시작하는 정점을 Queue에 넣는다. 그리고 Dequeue하며 Dequeue한 정점과 인접한 정점들을 Enqueue한다. 즉, 방문한 정점들을 순서대로 queue에 저장을 하는데 queue는 선입 선출이 원칙이기 때문에 가장 먼저 방문한 정점에 인접한 정점을 방문하게 된다. $O(V + E)$의 시간 복잡도를 갖는다. BFS로 구한 경로는 최단 경로이다.

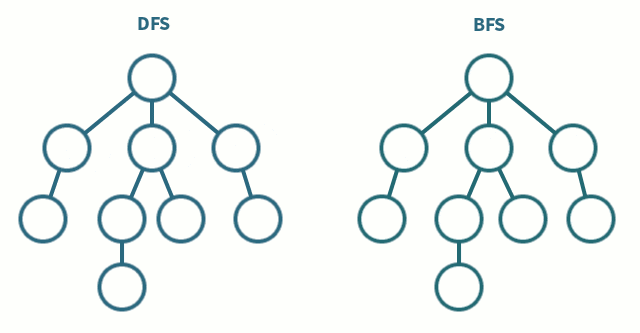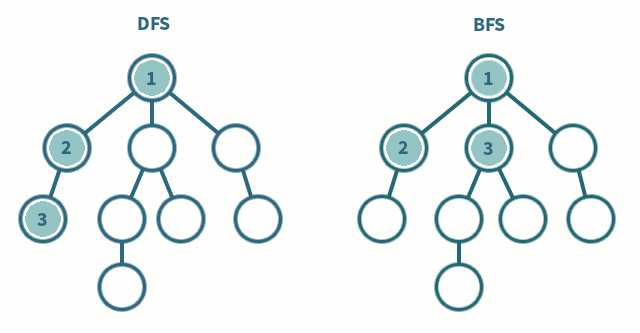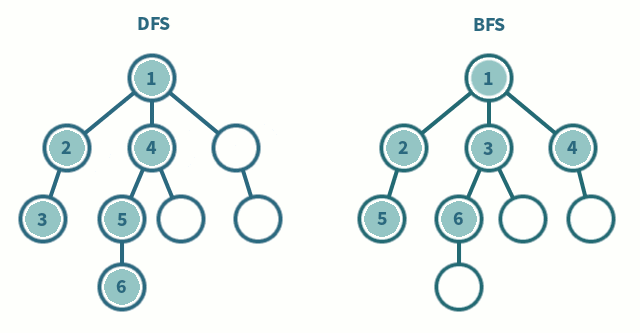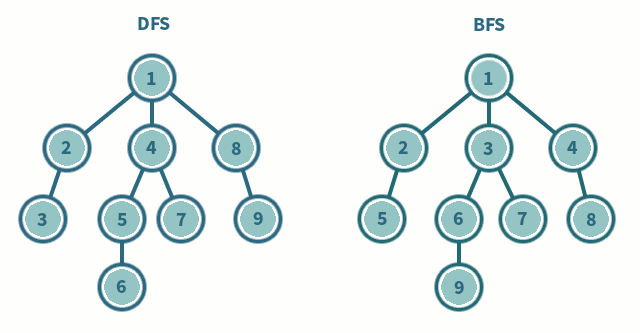
DFS와 BFS의 탐색 순서

MST(Minimum Spanning Tree, 최소비용신장트리)

  그래프 G의 Spanning Tree 중 가중치의 합이 최소인 Spanning Tree를 말한다. 여기서 말하는 Spanning Tree란 그래프 G의 모든 정점을 포함하고 Cycle이 존재하지 않는 그래프이다.

Kruskal Algorithm

 edge없이 vertex만 있는 상태에서 시작한다. Edge Set을 non-decresing으로 정렬한 후 가장 작은 weight에 해당하는 edge를 순서대로 추가한다. 이 때 사이클이 생기는 경우는 제외한다. 모든 vertex들이 연결되어 spanning tree가 완성되거나, 그래프가 완성될 수 없는 경우 모든 edge에 판단이 끝나면 종료된다.

어떻게 cycle 생성 여부를 판단하는가

 Graph의 각 vertex에 set-id라는 것을 추가적으로 부여한다. 그리고 초기화 과정에서 모두 1~n까지의 값으로 각각의 vertex들을 초기화 한다. 그리고 각 vectex들이 연결될 때 마다 set-id를 하나로 통일 시킨다. 두 set이 합쳐질 때 크기가 큰 set의 set-id로 통일시킨다.

시간 복잡도

1. 각 vertex에 대해 set-id를 부여한다 : $O(V)$
2. Edge의 weight를 기준으로 정렬한다 : $O(E\log E)$
3. 2에서 정렬된 Edge를 순차적으로 탐색한다 : $O(E)$

최종적으로 $O(E\log E)$의 시간 복잡도를 가진다.

Prim Algorithm

 초기화 과정에서 한 개의 vertex로 이루어진 초기 그래프 A를 구성한다. 그리고 나서 그래프 A 내부에 있는 vertex로 부터 외부에 있는 vertex 사이의 edge를 연결하는데 그 중 가장 작은 weight의 edge를 통해 연결되는 vertex를 추가한다. 어떤 vertex건 간에 상관없이 edge의 weight를 기준으로 연결한다. 이렇게 연결된 vertex는 그래프 A에 포함된다. 위 과정을 반복하고 모든 vertex들이 연결되면 종료한다.

시간복잡도

1. 각 vertex를 초기화 : $O(V)$
2. 최소 힙에서 가장 weight가 작은 노드(루트 노드)를 빼낸다, 이 때
   가장 말단 노드에 접근하여 가장 말단 노드를 루트 노드의 위치까지 가져와야 하므로 최대 높이($\log V$)만큼의 시간이 걸린다. 이 연산을 모든 $V$에 대해 수행한다 : $O(V\log V)$
3. 2와 동시에 모든 Edge의 weight정보를 업데이트 한다. 이 때 최소 힙을 탐색하기 때문에 한번 탐색 당 최대 $\log V$의 시간이 걸린다. 모든 Edge에 대해 탐색을 하기 때문에 최대 $E \log V$의 시간이 걸린다 : $O(E\log V)$

결과적으로 $O(V\log V + E\log V)$ 이지만, $E>V$이기 때문에 최종적으로 $O(E\log V)$의 시간 복잡도를 갖는다.