자바스크립트 알고리즘 Ⅰ

young-gue Park·2023년 1월 19일

JavaScript 이진탐색 정렬 탐색

JavaScript

목록 보기

9/20

⚡ 자바스크립트로 보는 알고리즘 Ⅰ

📌 정렬

🔷 요소들을 일정한 순서대로 열거하는 알고리즘

🔷 특징

① 정렬 기준은 사용자가 정할 수 있다.
② 크게 비교식과 분산식 정렬로 나눌 수 있다.
③ 대부분의 언어가 빌트인으로 제공해준다.
④ 삽입, 선택, 버블, 머지, 힙, 퀵 정렬 등 다양한 정렬 방식이 존재한다.

💡 정렬 방식은 상황에 따라 더 좋은 방식이 있을 뿐, 무조건 어떤 방식이 더 낫다 하는 것이 없다.

🌟 비교식 정렬

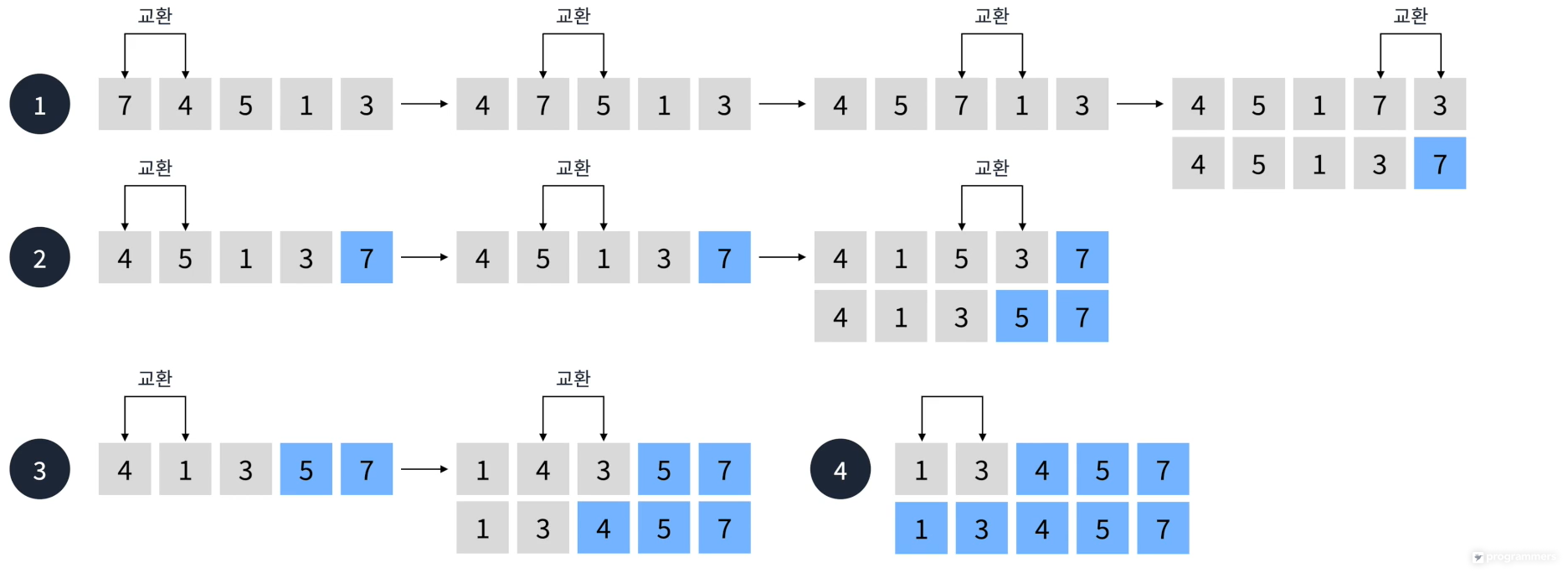
🔷 버블 정렬

서로 인접한 두 요소를 검사하여 정렬하는 알고리즘
O(n²)시간 복잡도를 가진다.

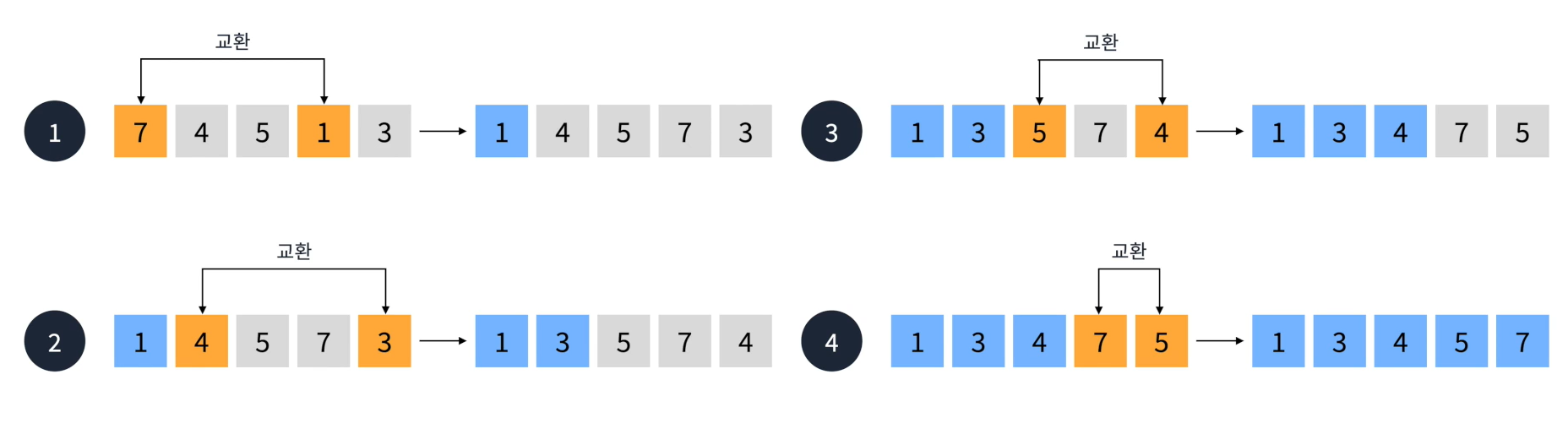
🔷 선택 정렬

선택한 요소와 가장 우선순위가 높은 요소를 교환하는 정렬 알고리즘
O(n²)시간 복잡도를 가진다.

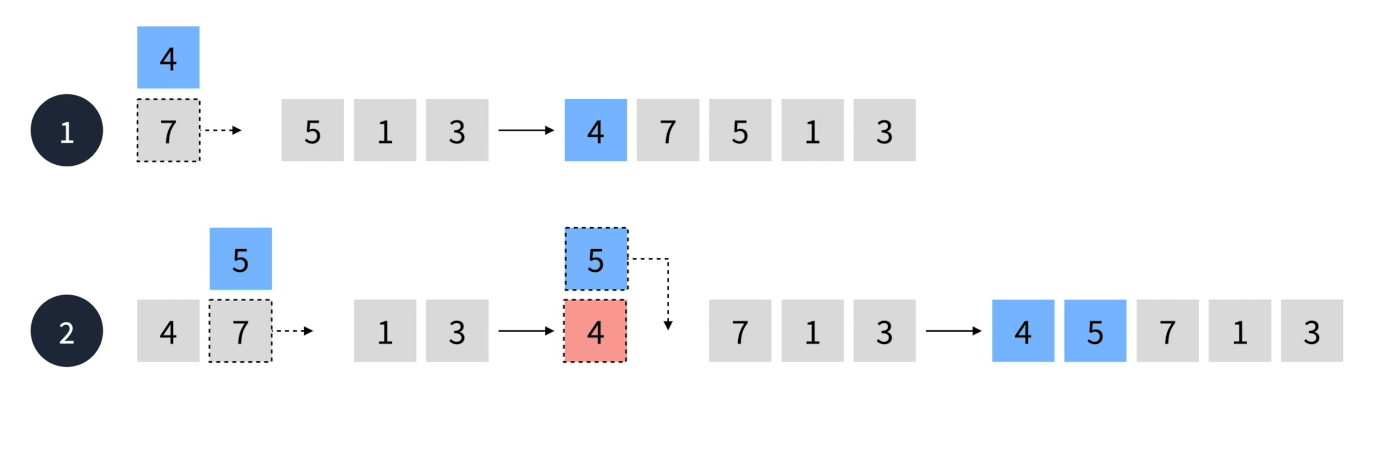
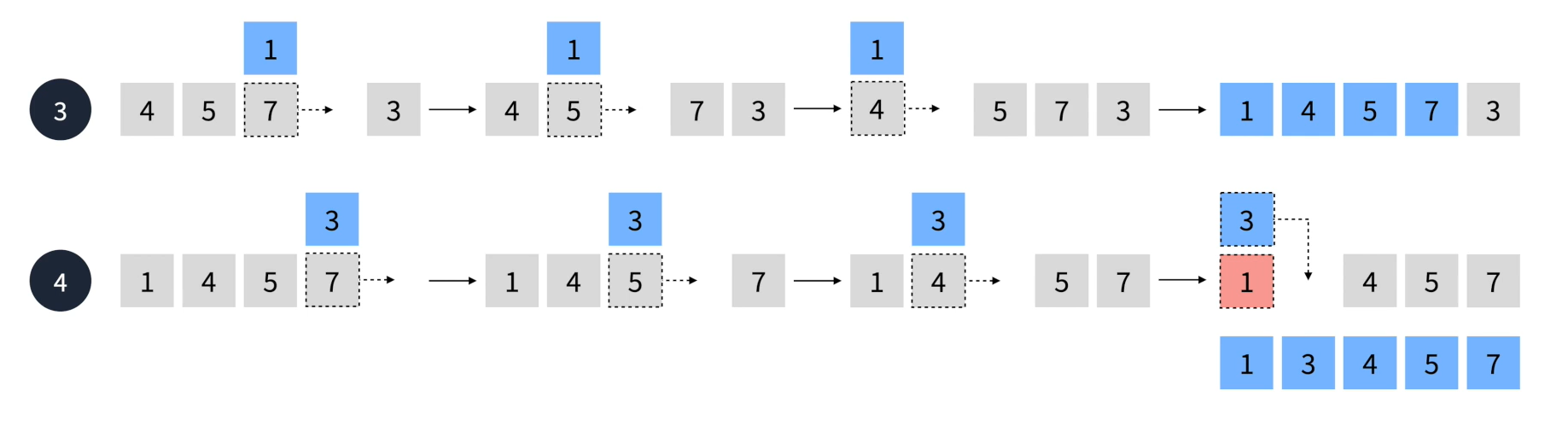
🔷 삽입 정렬

선택한 요소를 삽입할 수 있는 위치를 찾아 삽입하는 방식의 정렬 알고리즘
O(n²)시간 복잡도를 가진다.

🌟 분산식 정렬

🔷 분할 정복을 핵심 개념으로 삼는 정렬이다.

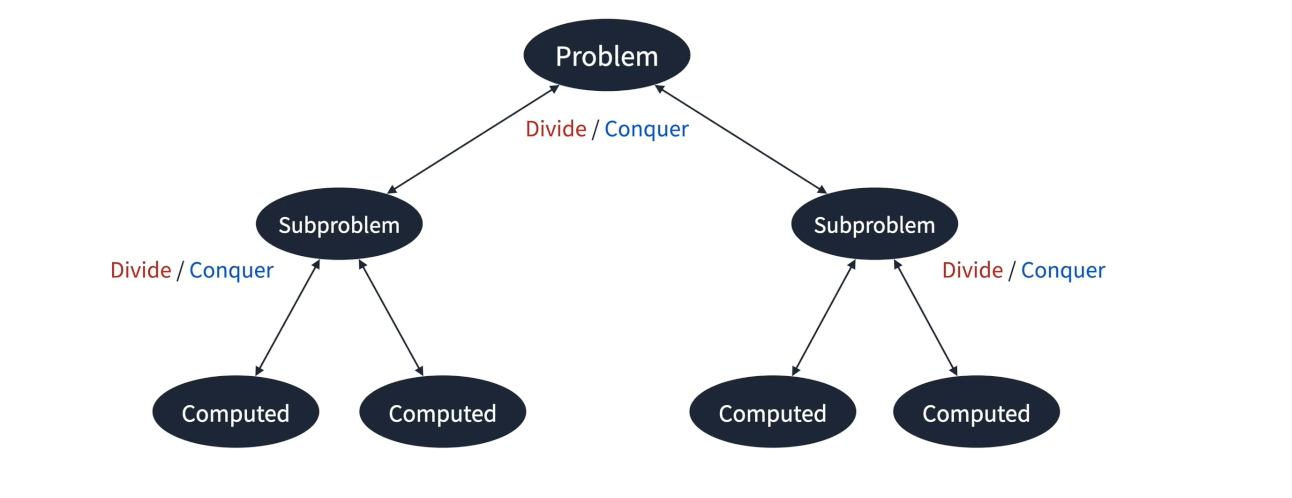
💡 분할 정복
문제를 작은 2개의 문제로 분리하고 더 이상 분리가 불가능할 때 처리한 후 합치는 전력, 다양한 알고리즘에 응용된다.

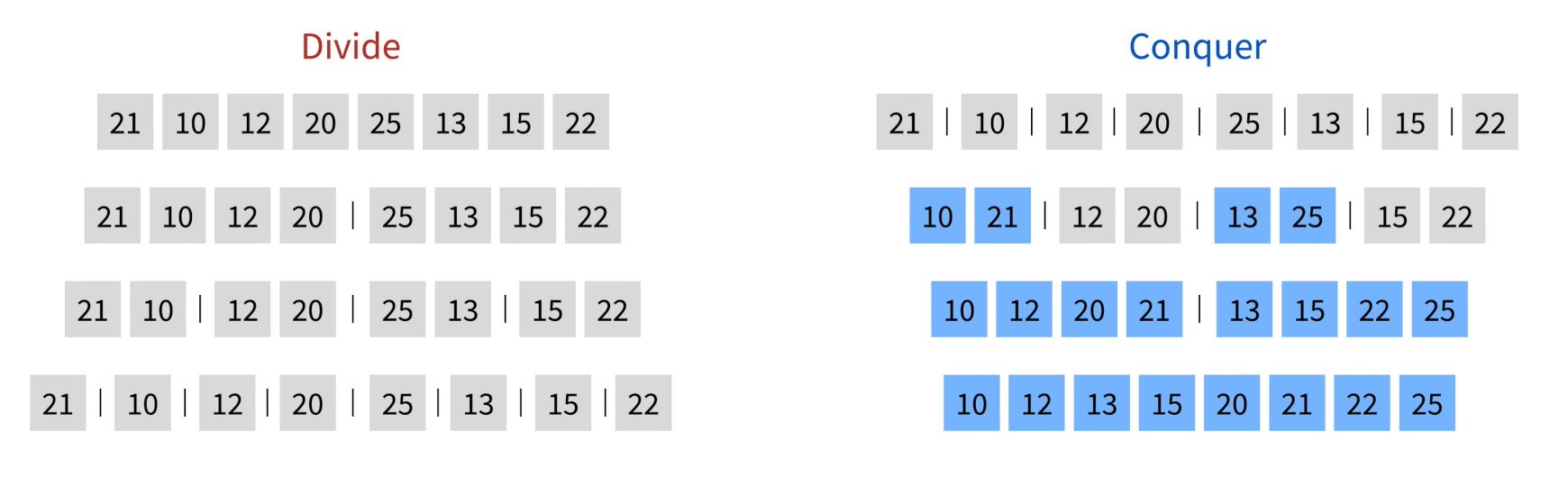
🔷 합병 정렬

분할 정복 알고리즘을 이용한 최선과 최악이 같은 안정적인 정렬 알고리즘
O(n log n) 시간복잡도를 가진다.

🔷 퀵 정렬

분할 정복 알고리즘을 이용한 매우 빠르지만 최악의 경우가 존재하는 불안정 정렬
O(n log n) 시간복잡도를 가진다.

🔷 자바스크립트에서의 정렬

Array.sort()를 이용하여 간단하게 구현할 수 있다.

// 정렬
// 그냥 정렬하면 아스키코드 순서로 정렬되어 원하는 숫자 크기대로 정렬되지 않는다.
const array3 = [5, 9, 10, 3, 8 ,3, 1];

array3.sort();
console.log(array3); // 아스키 문자 1이 2보다 작아 10이 먼저 나온다.

array3.sort((a,b) => a-b); // 오름차순 정렬
console.log(array3);

array3.sort((a,b) => b-a); // 내림차순 정렬
console.log(array3);

🖨 출력 결과

🤷‍♂️ 저 화살표 함수는 대체 뭔가요..?
함수 표현식보다 단순하고 간결한 문법으로 함수를 만들 수 있는 방법
함수 func는 화살표(=>) 우측의 표현식(expression)을 평가하고, 평가 결과를 반환한다.
예를 들어 화살표 함수 let sum = (a,b) => a+b는 다음 함수와 동일하다.
let sum = function(a, b) {
  return a + b;
};
화살표 함수는 this 예약어를 사용할 수 없는 등 다양한 특징이 있으니 기회가 되면 자세히 알아보도록 한다.

📌 이진 탐색

🔷 정렬 되어있는 요소들을 반씩 제외하며 찾는 알고리즘

O(log n) 만큼 시간복잡도가 걸린다.
선형 탐색보다 시간복잡도가 짧다는 장점이 있다.

💡 선형 탐색
요소들을 순서대로 하나씩 찾는 탐색 알고리즘으로, O(n) 시간복잡도가 걸린다.

🔷 특징

① 반드시 정렬이 되어있어야 사용할 수 있다.
② 배열 혹은 이진 트리를 이용하여 구현할 수 있다.
③ 시간복잡도가 짧은 만큼 상당히 빠르다.

🔷 구현

// 배열로 구현한 이진탐색
const array4 = [1, 1, 4, 126, 344, 633, 678, 1321, 5234];

function binarySearch(array, findValue) {
    let left = 0;
    let right = array.length - 1;
    let mid = Math.floor((left + right) / 2);
    while(left < right) {
        if(array[mid]===findValue) {
            return mid;
        }

        if (array[mid] < findValue) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
        mid = Math.floor((left + right) / 2);
    }
    return -1;
}

🖥 테스트 코드

// 이진탐색 테스트
console.log(binarySearch(array4, 1321));
console.log(binarySearch(array4, 1));
console.log(binarySearch(array4, 500));

🖨 출력 결과

💡 Math.floor()

매개 변수로 받은 숫자의 소수점 이하를 버림한다. 그 외에도
Math.ceil() : 매개 변수로 받은 숫자의 소수점 이하를 올림한다.
Math.round() : 매개 변수로 받은 숫자의 소수점 이하를 반올림한다.

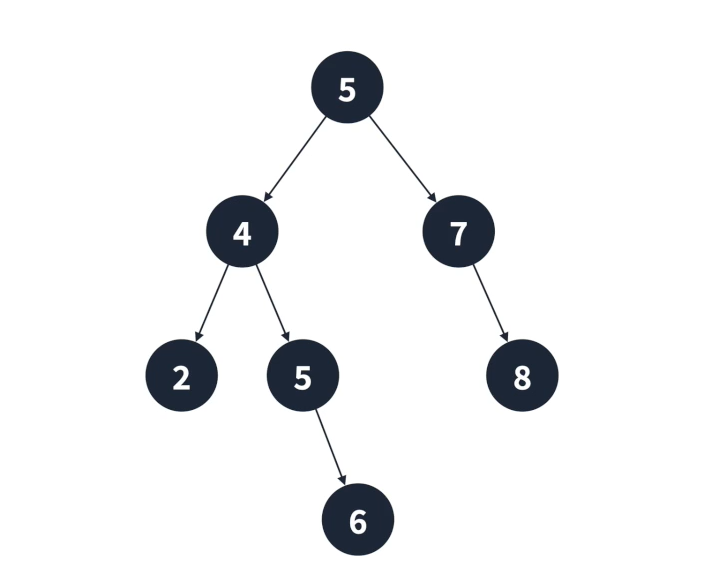
🔷 이진 탐색 트리

이진 탐색을 위한 이진 트리로 왼쪽 서브트리는 루트보다 작은 값이 모여있고, 오른쪽 서브 트리는 루트보다 큰 값이 모여있다.

문제점
① 최악의 경우 한쪽으로 편향된 트리가 될 수 있다. 이 때, 순차 탐색과 동일한 시간복잡도를 가진다.
② 이를 해결하기 위해 AVL 트리나 레드블랙 트리 같은 자료구조를 이용할 수 있다.

🔷 구현

class Node {
    constructor(value) {
        this.value = value;
        this.left = null;
        this.right = null;
    }
}

// 이진 탐색 트리
class BinarySearchTree {
    constructor() {
        this.root = null;
    }
    // 요소 삽입 알고리즘
    insert(value) {
        const newNode = new Node(value);
        if(this.root === null) {
            this.root = newNode;
            return;
        }

        let currentNode = this.root;
        while(currentNode !== null) {
            if(currentNode.value < value) {
                if(currentNode.right === null) {
                    currentNode.right = newNode;
                    break;
                }
                currentNode = currentNode.right;
            } else {
                if(currentNode.left === null) {
                    currentNode.left = newNode;
                    break;
                }
                currentNode = currentNode.left;
            }
        }
    }
    // 요소 제거 알고리즘
    remove(data) {
        this.root = this.removeNode(this.root, data);
    }
    removeNode(node, data) {
        if(node == null) {
            return null;
        }
        else if(data == node.data) {
            // 자식이 없을 때
            // 해당 노드를 null로 처리하고 그 노드를 return 한다.
            if(node.left == null && node.right == null) {
                node = null;
                return node;
            }
            // 왼쪽 자식이 없을 때
            // 오른쪽 자식을 해당 노드로 바꾸고 그 노드를 return 한다.
            if(node.left == null) {
                node = node.right;
                return node;
            }
            // 오른쪽 자식이 없을 때
            // 왼쪽 자식을 해당 노드로 바꾸고 그 노드를 return 한다.
            else if(node.right == null) {
                node = node.left;
                return node;
            }
            // 둘 다 자식이 있을 때
            // 삭제하려고 하는 노드를 오른쪽 서브트리 중 가장 작은 노드로 교체하고 해당 노드를 삭제한다.
            // 왼쪽 서브트리 중 가장 큰 노드로 교체할 수도 있다.
            let currentNode = this.findMinNode(node.right);
            node.data = currentNode.data;
            node.right = this.removeNode(node.right, currentNode.data);
            return node;
        } else if(data < node.data){
            node.left = this.removeNode(node.left, data);
            return node;
        } else{
            node.right = this.removeNode(node.right, data);
            return node;
        }
    }
    // 요소 제거 알고리즘을 위한 최소값 찾기 알고리즘
    findMinNode(node) {
        let currentNode = node;
        while(currentNode.left != null){
            currentNode = currentNode.left;
        }
        return currentNode;
    }

    has(value) {
        let currentNode = this.root;
        while(currentNode !== null) {
            if(currentNode.value == value) {
                return true;
            }

            if(currentNode.value < value) {
                currentNode = currentNode.right;
            } else {
                currentNode = currentNode.left;
            }
        }
        return false;
    }
}

🖥 테스트 코드

const binarySearchTree = new BinarySearchTree();
binarySearchTree.insert(9);
binarySearchTree.insert(4);
binarySearchTree.insert(6);
binarySearchTree.insert(3);
binarySearchTree.insert(2);
binarySearchTree.insert(7);
console.log(binarySearchTree.has(6));
console.log(binarySearchTree.has(4));
console.log(binarySearchTree.has(12));