[백준] #1074 Z⚡

• 백준 # 1074 Z
• 사용 언어 : C++
• 난이도 : 실버Ⅰ🥈

문제

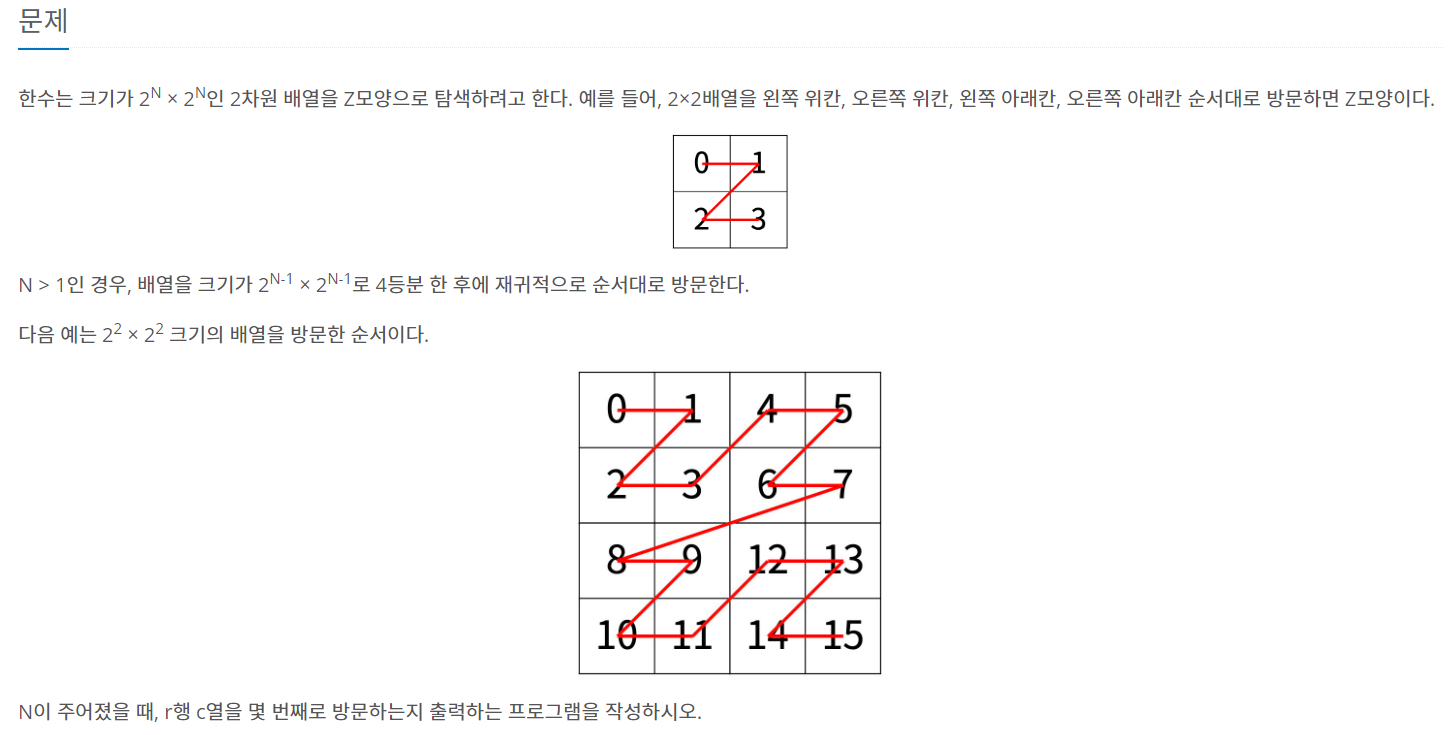
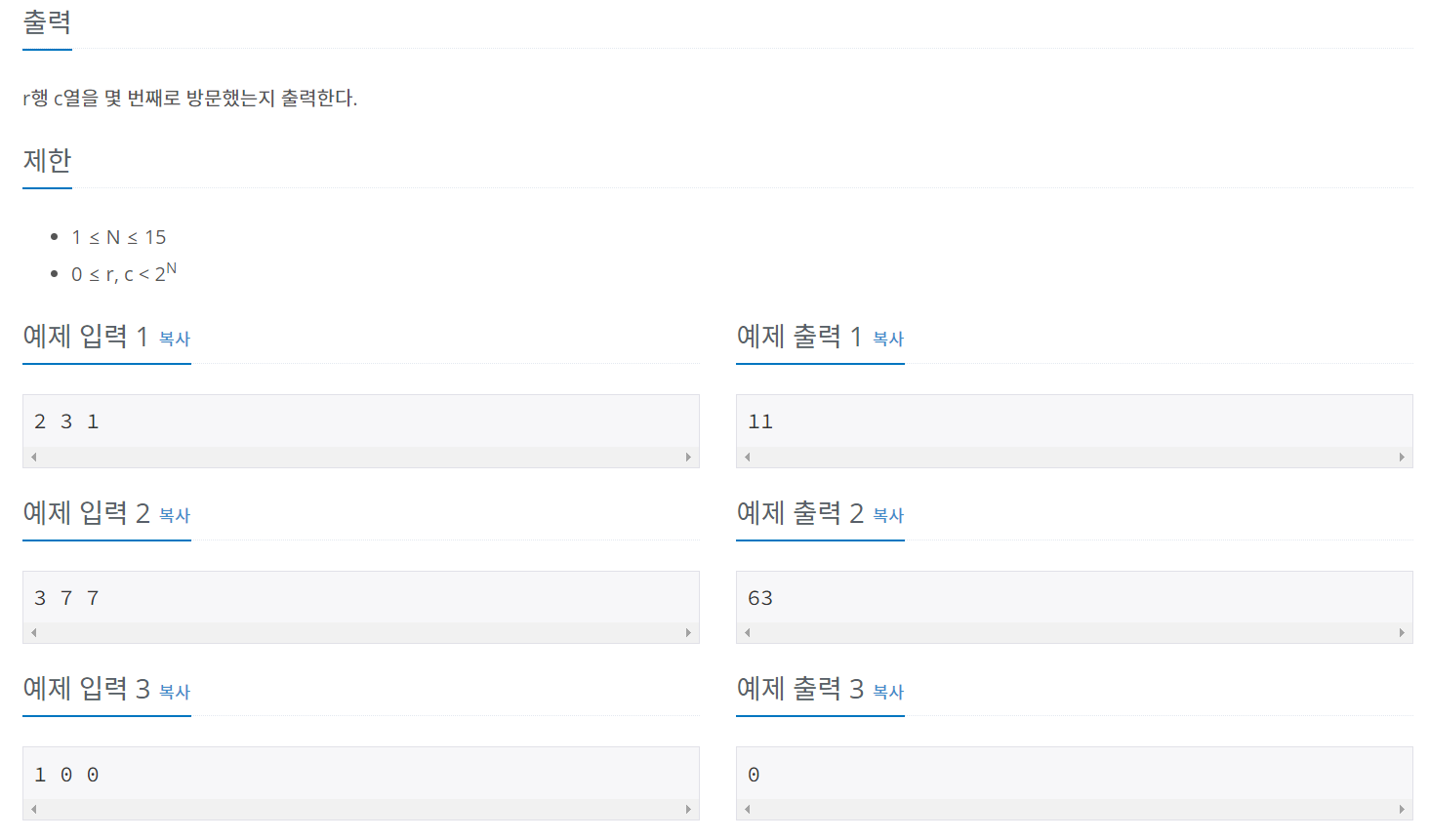
N과 r, c가 주어졌을 때, $2^N \times 2^N$ 배열에서, r행 c열은 몇번째로 방문되는지 출력하는 문제이다. 이 때 방문하는 방식은 위처럼 z모양이고, N>1인 경우에는 4등분하여 재귀적으로 z모양 순서로 방문하게 된다.

분석

우선 r행 c열에 도착할 때까지 하나하나 방문하여 그 횟수를 count할 것인지, 아니면 어떠한 연산을 통해 답을 구할 것인지를 결정해야 한다. 하나하나 count하게 되면 시간복잡도가 O(n)이다. 어떠한 연산을 통해 답을 구한다면, 아마 그 연산은 문제 자체에도 언급되었다시피 재귀를 이용한 방법일 것이다. 현재 N>1인 경우는 q배열을 4등분 하는데, 이때 연산 횟수가 1/4씩 줄어들게 되므로 O(logn)의 시간 복잡도를 가질 것이다. 문제에서 주어진 제한시간도 0.5초 이기 때문에, 후자의 방법을 사용하는 것이 적절할 것이다.

그렇다면 우리는 이 재귀문제를 풀기 위해, 어떤 것이 재귀적으로 반복되는지를 판단해야한다.
사실 난 애석하게도 수학적인 규칙을 찾는데에 젬병이기 때문에(...) 항상 예시를 먼저 분석하는 편이다.

이 문제의 핵심은 Z모양으로 움직이는 것이라 판단했다. 따라서 Z모양의 꼭짓점(시작점, 끝점, 꺾이는 지점)을 기준으로 좌표를 적어보았다.
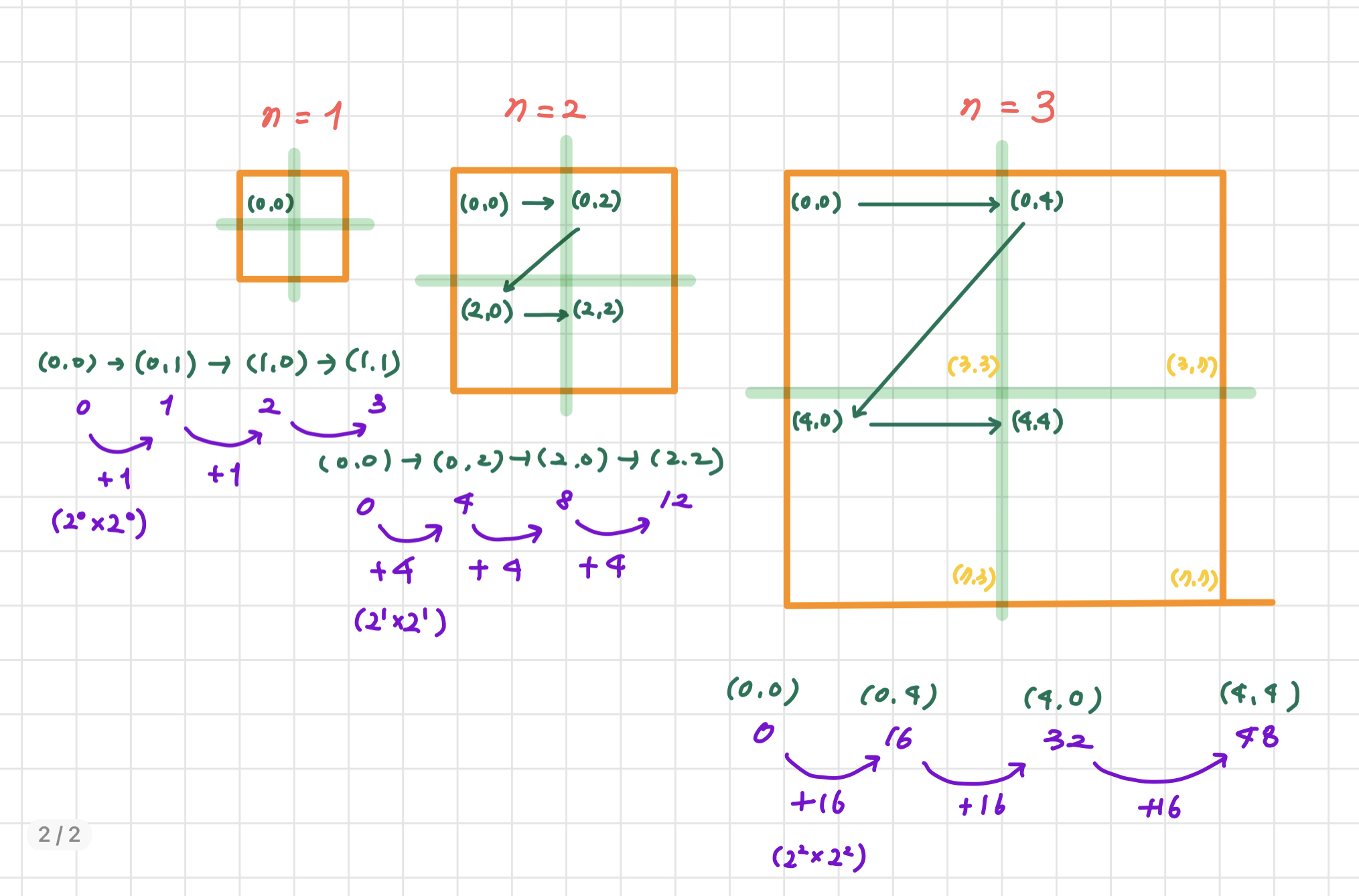보라색 숫자는 해당 좌표의 방문 순서를 의미한다. $2^{n-1}*2^{n-1}$ 씩 증가한다는 규칙을 찾을 수 있다.
그렇다면 r행 c열은 도대체 몇번째에 방문한 것일까?

우선 편의를 위해 n=3, r=5, c=5이라고 가정하자.
4등분한 사각형을 방문 순서대로 ①, ②, ③, ④라고 했을 때, 5행 5열은 ④에 존재한다. ④에서 가장 먼저 방문한 좌표가 48번째에 방문되는 것이므로, 5행 5열은 적어도 48번째 이후에 방문하게 된다.
그렇다면 우리는 ④에서 몇번째로 5행 5열이 방문되는지만 알면 된다. ④는 $2^{2}*2^{2}$ 크기이므로 n=2인 것과 동일하다.
그렇다면 n=2 라고 가정을 하고, 다시 4등분해서 동일한 과정을 반복하면 된다. 언제까지? 5행 5열에 다다를 때까지.

즉, 우리는 r행 c열이, 현재 포함된 구역을 4등분한 것 중 몇번째 구역에 있는지만 알아내면 된다. 구역의 포함여부를 알려면 각 구역의 좌표 범위를 알아야 한다! 이 또한 아래와 같이 분석해 보았다.

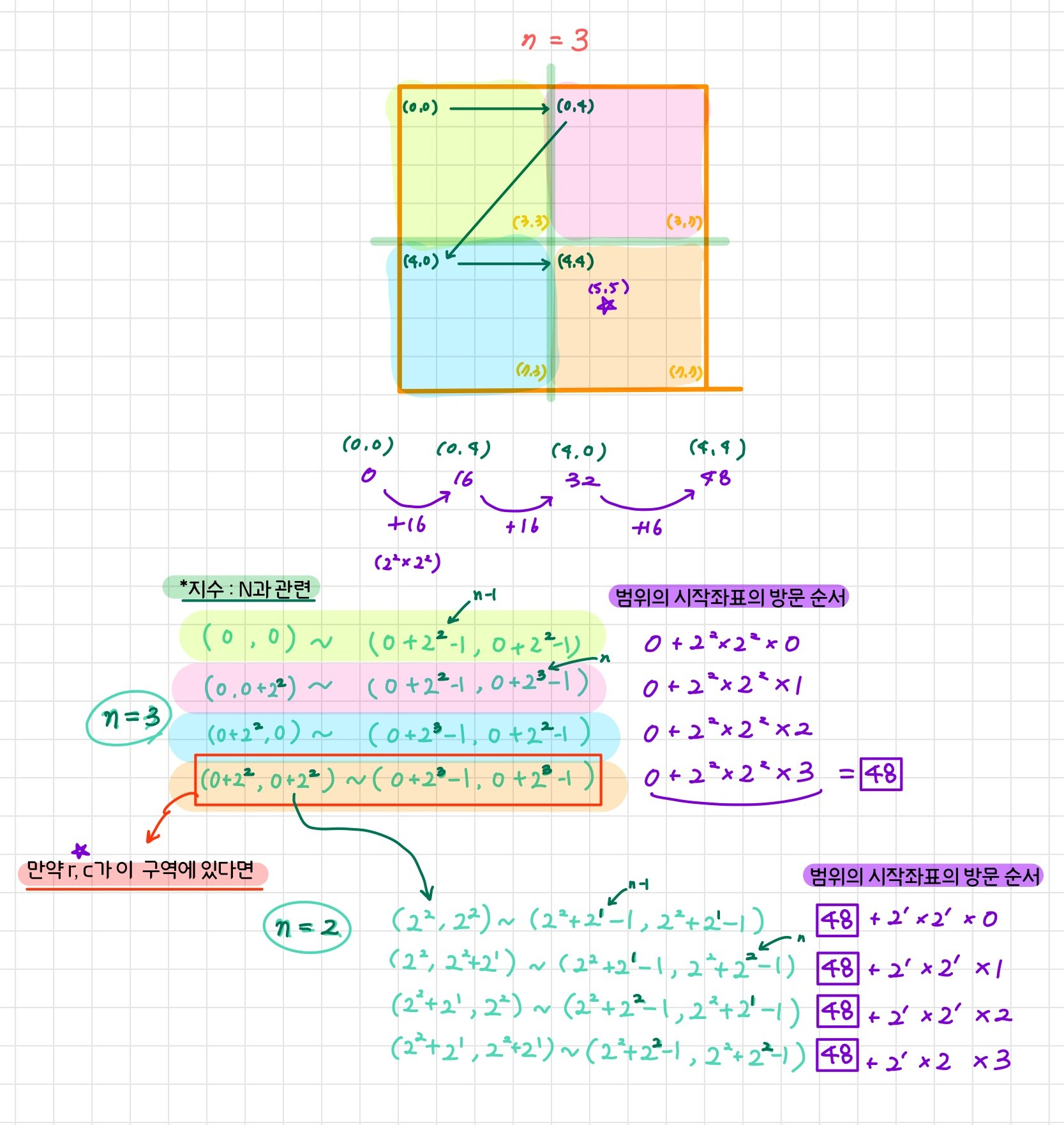
각 구역의 범위는 n값에 의해 결정이 된다.

첫 번째 구역의 시작점이 $(x,y)$라고 했을 때,
두 번째 구역의 시작점은 $(x+2^{n-1}, y)$ ,
세 번째 구역의 시작점은 $(x, y+2^{n-1})$ ,
네 번째 구역의 시작점은 $(x+2^{n-1}, y+2^{n-1})$

가 되고,

첫 번째 구역의 끝점은 $(x+2^{n-1}-1,y+2^{n-1}-1)$,
두 번째 구역의 끝점은 $(x+2^{n-1}-1,y+2^{n}-1)$,
세 번째 구역의 끝점은 $(x++2^{n}-1,y+2^{n-1}-1)$,
네 번째 구역의 끝점은 $(x+2^{n}-1,y+2^{n}-1)$,

가 된다.

규칙을 통해 시작점과 n값만 알면 구역의 시작, 끝 좌표를 알아낼 수 있게 되었으니, 이제는 단순하게 좌표를 비교하여 r행 c열이 네 구역중 어느 구역에 포함되는지를 판단하면 된다.

만약 r행 c열이 포함되는 구역을 찾았다면, 그 구역의 시작점을 $(x, y)$로 삼아 다시 구역을 나눠주면 된다.

방문 순서의 경우, 그림의 보라색 부분과 같이, 큰 구역의 시작좌표 방문 순서에다가, 다시 구역을 나누어 얻어진 작은 구역 중 포함되는 구역의 시작좌표 방문순서를 계속 더해주면 된다.

코드

위의 분석내용을 코드로 표현하면 아래와 같다.

#include <iostream>
#include <cmath>

using namespace std;
int N;
int r, c;

void z(int n,int x, int y, int* cnt);
int main()
{
    cin >> N >> r >> c;
    int cnt=0;
    z(N,0,0,&cnt);
    
    cout<<cnt;

    return 0;
}

void z(int n,int x, int y, int* cnt){
    if(n ==0){
        return;
    }
    
    // 각 구역의 시작 좌표 방문 순서 정할때 더해지는 값 
    int increase = exp2(n-1)*exp2(n-1);
    
    // 첫번째 구역
    if(r>= x && r<x + exp2(n-1) && c>= y && c<y+exp2(n-1)){
        *cnt+=0;
        z(n-1,x,y,cnt);
    }
    // 두번째 구역
    else if(r>= x && r<x + exp2(n-1) && c>= y+exp2(n-1) && c<y+exp2(n)){
        *cnt+=increase;
        z(n-1,x,y+exp2(n-1),cnt);
    }
    // 세번째 구역
    else if(r>= x+exp2(n-1) && r<x + exp2(n) && c>= y && c<y+exp2(n-1)){
        *cnt+=increase*2;
        z(n-1,x+exp2(n-1),y,cnt);
    }
    // 네번째 구역
    else{
        *cnt+=increase*3;
        z(n-1,x+exp2(n-1),y+exp2(n-1),cnt);
    }
    
}

느낀 점

분석을 꼼꼼히 했더니 한번에 풀린 문제! 근데 한번에 푼거치고는 설명이 굉장히...길었던 것같다. 다음에 재귀문제를 풀게 된다면, 수학적 귀납법으로 좀더 간단히 설명해보아야겠다.