
💻출처 : 프로그래머스 > 코딩 테스트 > Summer/Winter Coding(2019) > 멀쩡한 사각형
🏆난이도 : Level 2
📜 문제


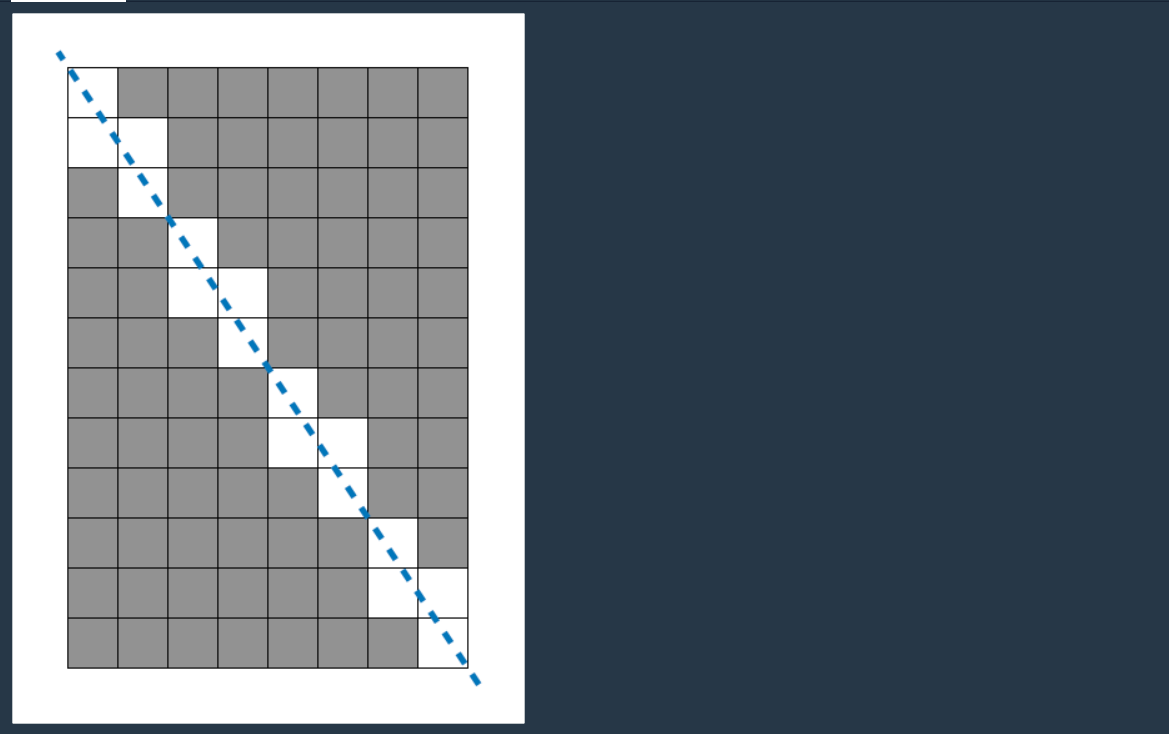
📝 요약
직사각형 종이를 대각선으로 자르면 두 개의 직각삼각형이 생긴다.
이 두개의 직각 삼각형에서 얻을 수 있는 1cm*1cm 크기의 정사각형 개수를 구하여라. 단, 각 정사각형의 가로, 세로는 원래 종이의 가로, 세로 방향과 평행해야 한다.
💡 아이디어 1 - O(WH)
직사각형을 대각선 방향으로 자르면 크기가 똑같은 직각 삼각형 두 개를 얻을 수 있다. 그럼 직각 삼각형 하나에 들어있는 정사각형 개수만 알면 되겠군!
따라서, 직각 삼각형에 정사각형을 그린 후, 해당 정사각형이 직각 삼각형 내부에 모두 포함되어있는지 판단하였다.
이를 판단하기 위해, 직각 삼각형을 아래 그림과 같이 모눈위에 올려놓았다.
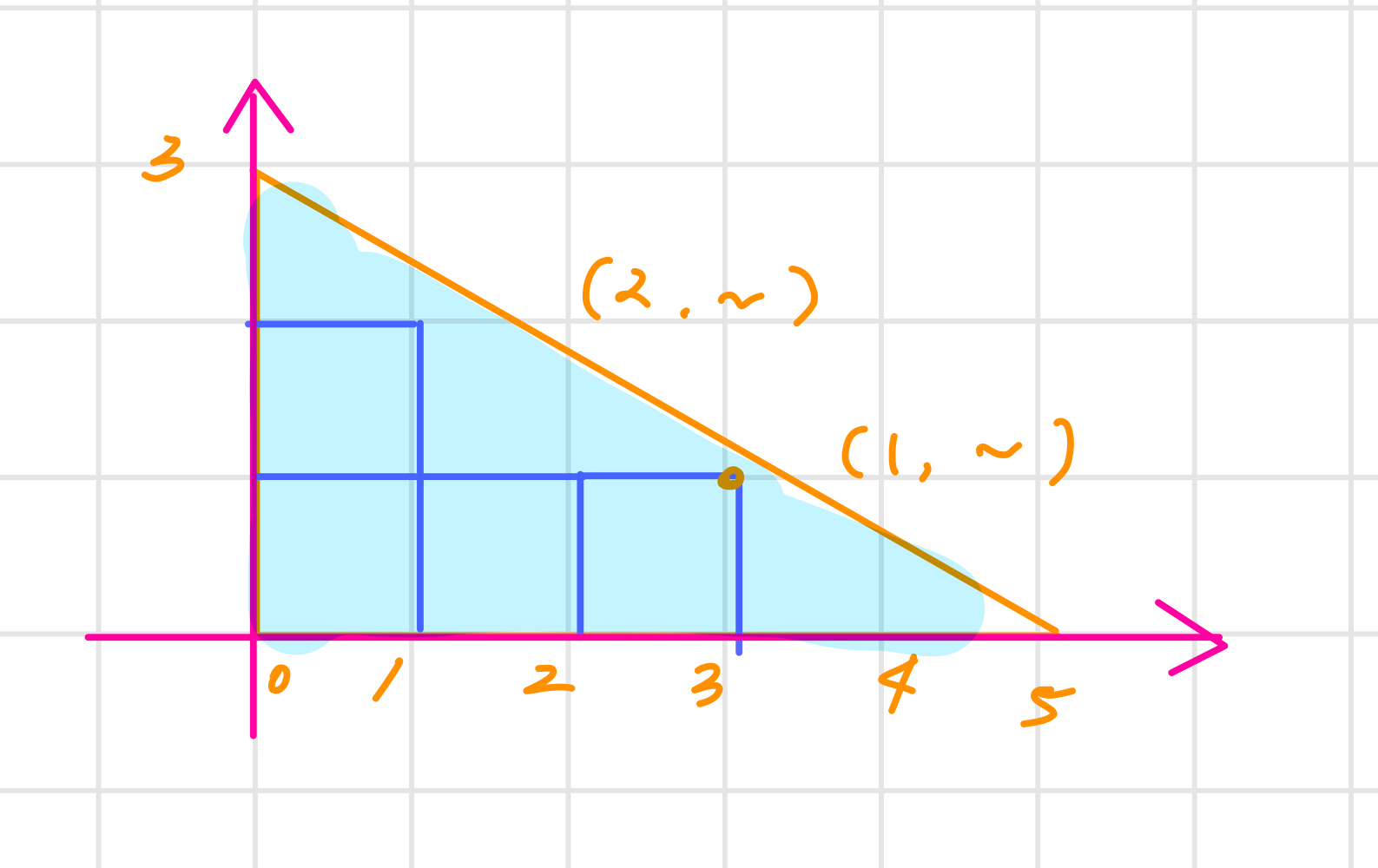
노란색 선을 직선의 방정식으로 표현한 뒤, 정사각형의 오른쪽 위 꼭짓점을 직선의 방정식에 대입해, 결과가 음수인지 양수인지에 따라 하늘색 영역에 포함되는지 여부를 판단하였다.
그럼 정사각형의 오른쪽 위 꼭짓점을 기준으로 본다고 정했으니까, (1,1) 있는 정사각형을 시작으로 for 문을 돌리면서, 하늘색 영역을 벗어날 때까지 사각형의 x좌표를 하나씩 증가시키면 되겠네? 만약 하늘색 영역을 벗어나면 y좌표를 증가시켜서 그 윗줄에 포함된 정사각형 개수를 구하면 되고!
아, 그런데 문제의 조건을 다시보자. w, h 의 범위는 1억 이하의 자연수이다.
...
이렇게 풀면 무조건 시간 초과다
그래서 문제를 다시 읽었더니 예시의 그림이 눈에 들어왔다.
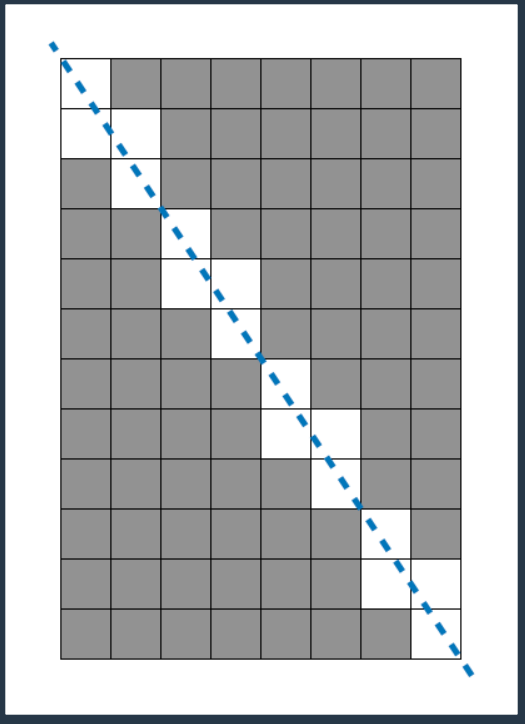
그림에서 약간의 힌트를 주고 있었다.
아, 대각선 부분에 걸쳐있는 사각형 개수만 구하면 되네!
그래서 아래의 방법을 생각하였다.
💡 아이디어 2 - 실제 풀이✅
이 방식은 컴퓨터 그래픽스의 rasterization 단계에서 사용하는 DDP 알고리즘과 유사하다. (수업 때 배운 걸 드디어 써먹는구나)
DDP 알고리즘의 경우, 대각선의 방향을 따라가며 대각선을 포함하는 정사각형을 찾는 알고리즘이다. 나는 DDP 알고리즘처럼 아래와 같은 규칙을 찾아보았다.
우선, 문제에서 준 예시와 달리 아래와 같이 사각형을 두고 생각하였다. (개인 취향)

이 사진을 보면, 대각선 위에 존재하는 정사각형의 옆이나 위, 그리고 대각선 위치(우상향 방향)에, 대각선 위에 있는 다른 정사각형이 존재한다는 것을 알 수 있다.
따라서, 정사각형의 오른쪽 위의 좌표가 (1,1)인 정사각형을 시작점으로 대각선을 따라 우상향 방향에 있는 정사각형을 보고, 대각선 위에 있는 정사각형의 특징을 알아냈다.
직사각형의 대각선의 기울기를 m이라고 하자.
현재 정사각형의 오른쪽 위 좌표를 (x,y) 라 했을 때,
w > h 인 직사각형에서는
x/y < m이라면 현재 정사각형의오른쪽 정사각형도 대각선에 포함되고,x/y > m이면, 현재 정사각형의위쪽 정사각형이 대각선에 포함되며,x/y == m이면, 현재 정사각형의오른쪽 위 대각선에 있는 정사각형이 대각선에 포함된다.
따라서, 나는 이러한 규칙을 이용하여 정사각형의 오른쪽 위의 좌표가 (1,1)인 정사각형을 시작점으로, 대각선 위에 있는 정사각형들의 개수를 모두 구했고, 전체 정사각형 개수에는 이를 제외하여 최종 결과를 얻었다.
참고 ❗
w < h인 경우는 규칙이 살짝 달라진다.
그러나, 위에 내용을 이해했다면 충분히 규칙을 찾을 수 있을 것이다.
직접 그려서 규칙을 찾으면 이해가 쉽다!
💻 코드
코드에서는 w < h 인 경우는 죄다 w > h로 변경하여 규칙을 통일해주었다.
풀이 코드는 아래와 같다.
function solution(width, height) {
var answer = 1;
let w = width;
let h = height;
if(w < h){ // 규칙 통일을 위해 w < h 인 경우, w > h로 변경
w = height;
h = width;
}
const m = w/h; // 기울기
let x=1; // 정사각형 시작 좌표
let y=1;
let count =0; // 대각선 위에 놓여 있는 정사각형 개수
while (x !== w || y !== h){
count++;
// 현재 정사각형의 위에 있는 정사각형이 대각선 위의 정사각형
if(m < x/y){
y++;
continue;
}
// 현재 정사각형의 대각선에 있는 정사각형이 대각선 위의 정사각형 (아래의 x++ 까지 실행함)
if(m == x/y) y ++;
x++; // if 문 모두 실행 안되는 경우 - 현재 정사각형의 오른쪽에 있는 정사각형이 대각선 위의 정사각형
}
count ++ ; // 최 우상단에 있는 정사각형 세어주기
answer = w*h - count;
return answer;
}
🎤 느낀 점
야심차게 생각했던 첫번째 아이디어는 무용지물이었다.
처음부터 문제의 조건과 예시를 주의 깊게 살펴보았다면, 허비되는 시간을 줄일 수 있었을 것이다😥
📌 결론 : 어떤 문제든 간에 문제를 잘 살펴보도록 하자!
