백준 tip (python)
기본 언어 변경하기
백준 페이지에서 설정 -> 언어 탭으로 넘어간다
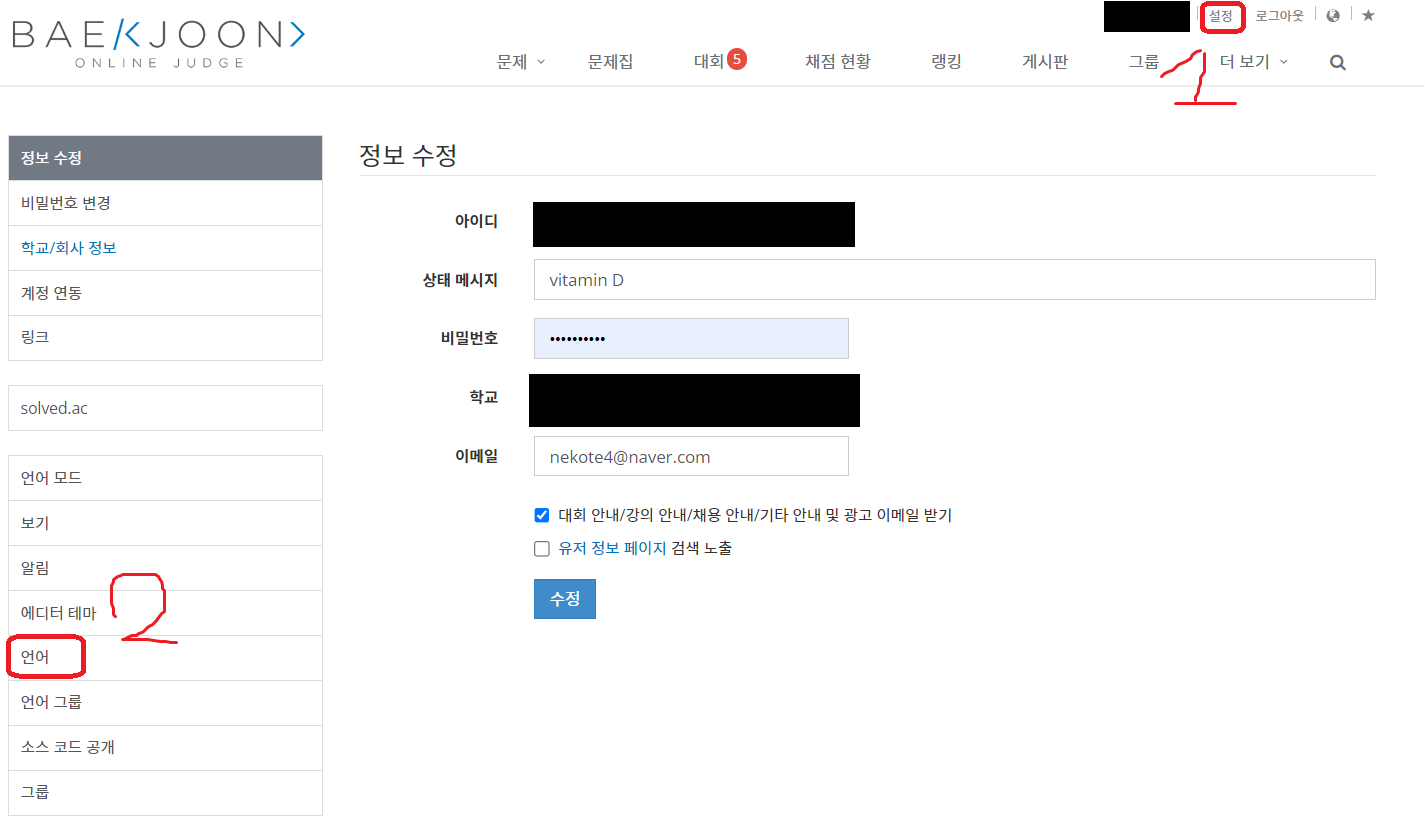
원하는 언어를 추가하거나 삭제하고, 최상단으로 올린다
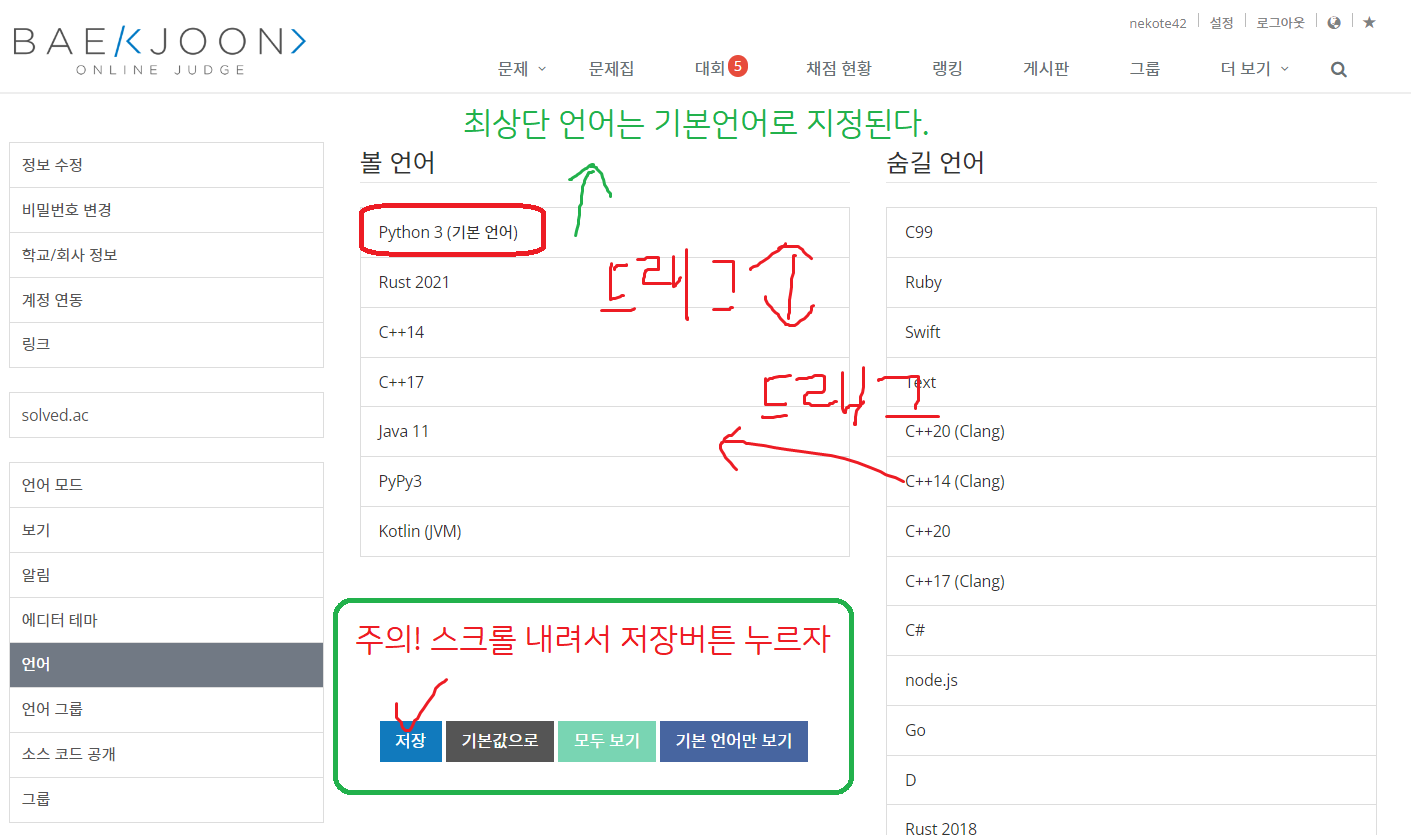
굿
map(int, input().split(' '))
[split()과 split(' ')의 차이](#split() 과 split(' ')의 차이)
open(0)
배열 초기화 방법
ㅁㄴㅇㄹ
solve=sum 이게 왜 되는거야??????
def solve(a):
...여다른 문제와는 다르게 solve 함수를 채워야 하는 내용인다
근데 이렇게 입력하면 성공한다
solve=sum대체 왜 되는걸까? solve=sum 이 작동하는 이유
정답은 alias와 관련이 있다.
# 우리가 작성한 solve 함수가 들어가는 부분
# 메인 코드 부분
# solve 함수를 호출하는 부분이렇게 있다고 가정해보자
def solve(a): 이게 solve=sum 으로 대체되는 순간
아래쪽 solve 함수를 호출하는 부분은 sum을 호출하게 된다.
그럼 뭐다? 사실상 sum(a)가 호출 되는것이고
이는 문제가 의도한 list내 모든 수의 합과 같으므로
통과가 된다.
팩토리얼을 매우 짧게 구현해보자
r=i=1;exec('r*=i;i+=1;'*int(input()));print(r)exec: 입력된 문자열 형태의 python code를 실행해준다.
'a' * int(): 문자열에 상수를 곱하면 상수배만큼 문자열이 반복된다.
숏코딩을 보면 효율적인 방법이 보인다
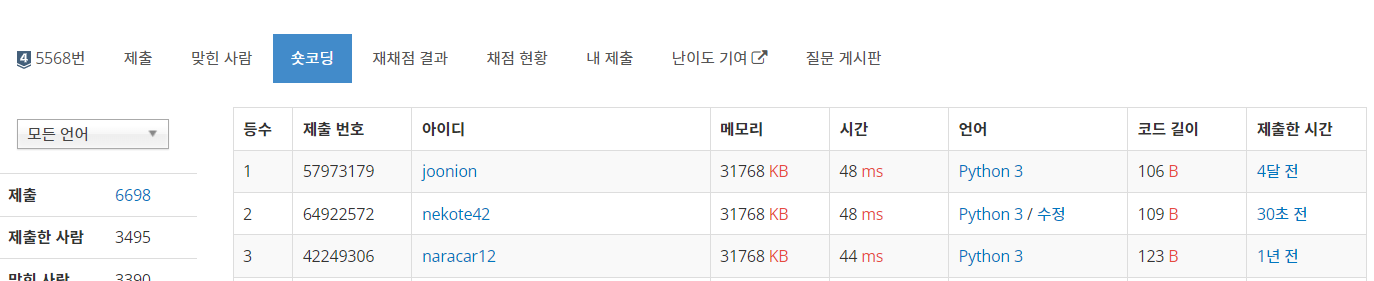
from itertools import*
n,k,*c=map(int,open(0))
print(len(set(''.join(map(str,p))for p in permutations(c,k))))python 공부
ord()
함수 alias
split() 과 split(' ')의 차이
result will contain no empty strings at the start or end if the string has leading or trailing whitespace.
python split reference
split()의 인자가 없으면(None) string의 앞, 뒤의 공백을 결과에 포함시키지 않는다.
max는 문자열의 대소도 비교할 수 있다.
print(max(input()[::-1].split()))
itertools: permutations(), combinations()
순열, 조합 모듈
xor 연산의 놀라움
tower = [1, 2, 3]
def f(a, b): # a = 1, b = 2
move(a, b)
move(a, 6-(a+b) # 6 - (1 + 2) = 3
move(b, a^b) # a^b = 3
# 1: 0b0001
# 2: 0b0010
# 3: 0b0011
# 2 xor 3 = 1
하노이의 탑 문제를 풀면서 알게된 xor연산 활용방법
XOR 연산에 대해 정의를 내리자면
서로 다른 부분(bit)를 기록(mark)한다.
내지는
차이를 기록했다
정도로 이해했다.
예를들어 A XOR B = C 라고 하자
A는 B와의 차이를 C를 통해 알 수 있다.
그렇다면 A는 B가 되기 위해서는 C에서 표기된 부분(bit)만 반전시키면 될 것 아닌가!
고로 A XOR C = B 라고 할 수 있다.
문제풀이
달팽이는 올라가고 싶다!
https://www.acmicpc.net/problem/2869
a,b,v=map(int,input().split());
print(1-(v-a)//(b-a))
# 또는
print((v-a-1)//(a-b)+2)
골드바흐의 추측
https://www.acmicpc.net/problem/9020
소수를 미리 구해놓고 이를 활용하는 방식으로 풀었다.
# 에라토스테네스의 체
def get_primes_until_n(n: int):
is_prime = [False, False] + [True] * (n - 1)
primes = []
for i in range(2, n + 1):
if is_prime[i]:
primes.append(i)
for j in range(2 * i, n + 1, i):
is_prime[j] = False
return primes# x = a + b 를 만족할 때 b, x-b 가 각각 소수인지 판별할 경우
for i in range(x//2, x):
if x-i in primes and i in primes:
print(f'{x-i} {i}')
break
# x = a + b를 만족할때 각각 +1, -1을 수행하며 소수인지 판별할 경우
a = b = x // 2
while a > 1:
if a in primes and b in primes:
break
a -= 1
b += 1
print(f'{a} {b}')
풀이 결과

8ms 차이가 났다. 큰 의미는 없어 보인다.
문제를 풀면서 혹시라도 +1, -1을 수행하며 소수의 합을 찾는 데 없으면 어떡하나? 라는 생각을 했다.
물론 사전 정의에 의하면 반드시 하나 이상은 조합이 나오는데, 확신이 안서서 반례찾는 코드를 작성해봤다.
def find_prime_pair(primes, x):
for i in range(x // 2, x):
if x - i in primes and i in primes:
return True
return False
n = 100000
primes = get_primes_until_n(n)
for i in range(4, n+1, 2):
if not find_prime_pair(primes, i):
print(i)
물론 n = 10000 까지 해봤는데 너무 잘된다.
