Improving Position Encoding of Transformers for Multivariate Time Series Classification

cacbon_dioxit·2025년 2월 18일
convtran
0

이 포스트에서는 "Improving Position Encoding of Transformers for Multivariate Time Series Classification"라는 논문을 제 나름대로 인공지능 스터디 발표(20240602, 20240626)를 위해 리뷰를 적었던 것입니다. 잠시 회사 다닐 때 이 논문에서 제시된 ConvTran 모델을 잘 이용한 적 있습니다.

https://link.springer.com/content/pdf/10.1007/s10618-023-00948-2.pdf

Abstract

  • 시계열 데이터에서 트랜스포머를 응용하려면 효과적인 포지션 인코딩이 필요하다.
    • 포지션 인코딩은 데이터의 순서와 관련있는 인코딩임
    • 이는 여전히 논란이 많은 주제이다.
    • 논문의 저자는 일반화 성능을 높이기 위해 tAPE, eRPE라는 새로운 방법을 제시했다.
    • 그리고는 tAPE/eRPE와 콘볼루션 기반의 입력 인코딩 방식을 결합하여 만든 다변량 시계열 분류 모델인 ConvTran을 제안하였다.
  • 제안된 인코딩 방법은 단순하면서도 효과적이다. 트랜스포머의 블록에도 통합하기 쉽고, 기타 다운스트림 태스크에도 효과적이다.
    • 다운스트림 태스크: forecasting, extrinsic regression, anomaly detection
    • 기존 SOTA 모델보다 더 높은 정확도 보임

1. Introduction

  • 많은 분야에서 시계열 분석을 필요로 하는데, 대부분은 본질적으로 다변수적인 성격을 내재하고 있다.
    • 다변량 시계열 기반 분류 모델 등은 현재 큰 관심이 쏠리는 분야이다.
  • CNN 모델이 효과적인 부분도 있으나(지역적 특징 추출), 그 구조 상 장기 의존성(long-range dependencies)를 잡아낼 수 없다.
  • LSTM 등과 같은 RNN 계열의 모델이 그러한 부분을 포착해내긴 하지만, 계산 비용이 높은 데다가, 장기 의존성을 짚어내는 데에 한계가 있다.
  • 반면 어텐션 모델은 장기 의존성을 잡아낼 수 있고, 그로 인해 문맥적인 정보를 제공할 수 있다.
    • 자연어 처리 분야에서 어텐션 모델이 성공하자 컴퓨터 비전, 시계열 분석 등에도 어텐션 모델을 도입하려는 시도가 우후죽순 생겨났다.
  • 트랜스포머 모델의 핵심은 셀프 어텐션이며, 시계열 입력 데이터의 관계를 모델링하는 데에 능하다.
    • 그러나 한계도 있는데, 바로 입력의 순서를 포착하지 못한다는 것이다.
    • 그러한 위치 정보를 명시적으로 표현해주어 덧붙이는 것은 어텐션 모델에서 중요하다.
  • 트랜스포머에서 위치 정보를 인코딩하는 데에는 두 가지 주요 방법이 있다.
    • Absolute Method: 시퀀스(순서, 서열, 수열) 내 절대적인 위치에 기반하여 서로 다른 인코딩 벡터를 각 위치에 할당하는 방법
    • Relative Method: 절대적인 위치보다는 시퀀스 내 두 원소의 상대적인 거리를 인코딩한다.
  • 포지션 인코딩은 자연어 처리, 컴퓨터 비전 등의 분야에서 효과적인 것으로 입증되었다. 그러나 시계열 분석에서는 그 효과가 여전히 불분명한 것으로 남아있다.
    • 기존의 absolute position encoding은 언어 모델을 위해 제안된 것인데, 그런 모델에서는 입력이 주로 512차원, 1024차원처럼 높은 임베딩 차원을 가진다.
    • 시계열 분류 모델에서는 임베딩의 차원이 상대적으로 낮고, 입력 데이터의 길이도 천차만별이라서, 자연어 처리에서와 차이점이 있다.
  • 이 논문에서는 최초로, 기존의 absolute & relative position encoding 방법이 시계열 데이터에 얼마나 효과적인지(다시 말해 그 인코딩이 의도한 목적을 잘 달성하는지)를 연구하였다.
    • 그리고 기존의 absolute position encoding이 시계열 데이터에서는 효과적이지 않음을 보일 것이다.
      • 저자는 임베딩의 차원과 시간의 길이를 반영하는, 시계열 데이터에 특화된 새로운 absolute position encoding 방법을 소개한다.
      • 저자는 새로운 absolute position encoding 방법이 기존의 방법보다 더 좋은 퍼포먼스를 냄을 보일 것이다.
    • 추가적으로, 기존의 relative position encoding 방법은 메모리 오버헤드가 너무 크고 학습시킬 파라미터 수가 많기 때문에 과적합되기 쉽다.
      • 저자는 시계열 분야에서 일반화 성능을 높이기 위한 계산 효율적인, 새로운 relative position encoding을 제안한다.
      • 저자는 새로운 relative position encoding 방법이 기존의 relative position encoding 방법보다 더 좋은 퍼포먼스를 냄을 보일 것이다.
    • 저자는 더 나아가, absolute/relative position encoding 방법의 조합에 기반을 둔 새로운 시계열 분류 모델(ConvTran)을 제안한다.
      • 32개의 벤치마크 데이터셋에 대한 실험을 통해 ConvTran이 이전 SOTA보다 유의미하게 더 정확한 결과를 냄

2. Related Works

3. Background

이 장에서는 셀프 어텐션과 현재 쓰이는 포지션 인코딩 방법들을 알아본다.

3.1 Problem Description and Notation

  • n개의 샘플이 있는 시계열 데이터셋 X={x1,x2,…,xn}X = \{ \bold{x}_1, \bold{x}_2, … , \bold{x}_n \}이 있고,
    • 각 xt={x1,x2,…,xL}\bold{x}_t = \{x_1, x_2, … , x_L\}은 dxd_x차원의 시계열 데이터(xi∈Rdx,xt∈RL×dxx_i \in \mathbb{R}^{d_x}, \bold{x}_t \in \mathbb{R}^{L \times d_x})이고
    • LL은 시간의 길이이다.
  • 그리고 대응되는 label의 집합 Y={y1,y2,…,yn}Y = \{y_1, y_2, … , y_n \}이 존재하며
    • 각 yt∈{1,…,c}y_t \in \{ 1, … , c \}이고 cc는 클래스의 개수이다.
  • 우리의 목표는 X에서 Y로 사상하는 뉴럴 네트워크 분류기를 훈련시키는 것이다.

3.2 Self-Attention

  • 셀프 어텐션은 본래 자연어 처리를 위해 고안된 것이다.
    • 원래는 RNN, CNN 등에 어텐션을 붙여서 주로 쓰다가, Vaswani가 순수하게 셀프-어텐션에만 의존하는 “트랜스포머 모델”을 제안하였다.
    • 추가: “어텐션”은 말 그대로 자연어 문장 중 특정 부분에 더 두드러지게 “집중”한다는 뜻이고, 이는 특정 부분에 더 가중치를 준다는 뜻이다.
  • 트랜스포머 모델은 쿼리, 키-밸류 쌍을 입력받아서 출력을 내보낸다.

    • 더 구체적으로, 입력 series xt={x1,x2,…,xL}\bold{x}_t = \{x_1, x_2, … , x_L\}에 대해 셀프 어텐션은 출력 series zt={z1,z2,…,zL}\bold{z}_t = \{z_1, z_2, … , z_L\}을 계산하여 내보낸다.

    • 이 때 zi∈Rdzz_i \in \mathbb{R}^{d_z}이며, 입력 series의 elements들의 가중합(weighted sum)으로 계산된다.

      zi=∑j=1Lαi,j(xjWV)z_i = \sum_{j=1}^{L} \alpha _{i, j} (x_j W^V)

    • 위에서 각 가중치 계수 αi,j\alpha _{i, j}는 softmax 함수를 통해 계산된다.

      αi,j=exp⁡(eij)∑k=1Lexp⁡(eik)\alpha_ {i, j} = \frac{\exp(e_{ij})}{\sum_{k=1}^L \exp(e_{ik})}

    • 여기서 eije_{ij}는 j 위치에서 i 위치로의 어텐션 가중치이며, scaled dot-product(내적)를 통해 계산된다.

      eij=(xiWQ)(xjWK)Tdze_{ij} = \frac{(x_i W^Q)(x_j W^K)^T}{\sqrt{d_z}}
      • 추가: 내적 값은 계속해서 커질 수 있다. 벡터 qq, kk의 원소가 평균이 0이고 분산이 1인 확률변수라고 가정할 때, qq와 kk의 내적은 평균이 0이고 분산이 dkd_k이며 표준편차는 dk\sqrt{d_k}이다. 이렇게 내적 값이 커지면, 이 값을 입력받는 위의 softmax 함수는 그래디언트가 매우 작아지게 된다. 이를 방지하기 위해 스케일링 과정을 거쳐준다.

    • 위의 사영 WQ,WK,WV∈Rdx×dzW^Q, W^K, W^V \in \mathbb{R}^{d_x \times d_z}은 파라미터 행렬이며, 각 레이어마다 유일하다.

      • 셀프 어텐션을 한 번 해주는 것보다, 멀티-헤드 어텐션(MHA)를 이용해 셀프 어텐션을 병렬적으로 처리할 수 있다. 멀티-헤드 어텐션의 출력에도 선형 변환이 관여되며, 각 셀프 어텐션의 출력을 concatenate한 것(이어 붙인 것)이다.
      • 추가: 사영은 선형 변환이다.

3.3 Position Encoding

  • 트랜스포머 모델의 셀프 어텐션 레이어는 입력 데이터의 순서를 보존할 수 없다. (CNN의 컨볼루션 연산이나 RNN의 순환 등이 없기 때문에)
    • 그래서 보통 트랜스포머를 이용한 방법론에서는 입력 데이터에 순서와 관련된 정보를 추가해준다. (absolute positional encoding, relative positional encoding 등)

3.3.1 Absolute Position Encoding

  • 원조의 셀프 어텐션은 “절대 위치”—상대적인 위치가 아니라—를 고려하며, 입력 임베딩 xx에다가 포지션 임베딩 P=(p1,…,pL)P=(p_1, … , p_L)을 더해준다.
    xi=xi+pix_i = x_i + p_i
    • 여기서 각 포지션 임베딩 pi∈Rdmodelp_i \in \mathbb{R}^{d_{model}}이다.
  • Absolute positional encoding 방법에는 여러 선택지가 있다.
    • 고정된 인코딩을 이용: 삼각함수 적용
      pi(2k)=sin(iωk), pi(2k+1)=cos(iωk), ωk=10000−2k/dmodelp_i(2k) = sin(i\omega_k), \ p_i(2k+1) = cos(i\omega_k), \ \omega_k = 10000^{-2k/d_{model}}
      여기서 kk는 [0,dmodel2]\left [ 0, \frac{d_{model}} {2} \right ]의 범위에 있고, dmodeld_{model}은 임베딩의 차원이며 ωk\omega_k는 삼각함수의 주파수(주기)와 관련된 것이다.
    • 학습시켜서 얻은 인코딩을 이용
    • 추가: Attention is all you need의 논문에 따르면 두 가지 방법을 다 해보니 거의 동일한 결과가 나와서 삼각함수를 이용한 인코딩을 선택했다고 한다.

3.3.2 Relative Position Encoding

  • Absolute position encoding에 덧붙여, 최근의 자연어 처리와 컴퓨터 비전 연구에서는 입력 벡터의 두 위치 사이의 관계(i.e., “상대적인 위치”에 따른 관계)를 동시에 고려하고 있다.
    • 이러한 방법은 입력 벡터의 각 요소 xi,xjx_i, x_j 사이의 상대적 거리를 인코딩하여 pi,jQ,pi,jK,pi,jV∈Rdzp_{i, j}^Q, p_{i, j}^K, p_{i, j}^V \in \mathbb{R}^{d_z} 를 만든다.
    • 위의 인코딩 벡터는 셀프-어텐션 모듈에 그대로 넣어서 활용한다.
      zi=∑j=1Lαi,j(xjWV+pi,jV)z_i = \sum _{j=1}^L \alpha_{i,j}(x_j W^V + p_{i,j}^V)
      eij=(xiWQ+pi,jQ)(xjWK+pi,jK)Tdze_{ij}=\frac{(x_i W^Q+p_{i,j}^Q)(x_jW^K+p_{i,j}^K)^T}{\sqrt{d_z}}
    • 이러한 방식을 사용하면 트랜스포머가 학습되면서 상호 간 위치적 관계가 학습된다.
    • Shaw et al. 에서 최초로 셀프-어텐션을 위한 relative position encoding을 제안하였다.
    • Huang et al. 에서 Shaw et al.에서의 메모리 비효율성을 보완한 방법을 제안하였다.

4 Position Encoding of Transformers for Multivariate Time Series Classification

  • 트랜스포머 기반 시계열 분류를 다룬 선행 연구에서 잘 다뤄지지 않은 몇 가지 측면을 설명하기 위해 저자들은 새로운 포지션 인코딩 방식을 설계하였다.
    • 그 첫 단계로써 새로운 absolute position encoding 방식인 tAPE(time Absolute Position Encoding)을 제안하였다.
      • tAPE는 series의 길이와 입력 임베딩 차원을 포함한다.
    • 그 다음으로 저자는 eRPE(efficient Relative Position Encoding)을 제안하였다.
      • 상대적 위치를 인코딩하기 위한 여러 방법을 연구해보았고, 가장 효과적인 방법을 찾았다.

4.1 Time Absolute Position Encoding (tAPE)

  • Absolute Position encoding은 본래 언어 모델링을 위해 제안된 것인데, 임베딩 벡터의 차원이 512 또는 1024와 같이 매우 높다는 특징이 있다. (입력의 길이는 512)
    • 논문의 figure 1a를 보면 512와 같은 높은 임베딩 차원에서 삼각함수 인코딩이 여러 위치 간의 거리를 잘 반영함을 알 수 있음 (논문 저자는 이를 “distance awareness property”라고 칭했음)
    • 그런데 임베딩 차원이 64 등으로 작아지면 두 위치 간의 거리가 커짐에 따라 dot-product가 항상 커지지는 않았다.
      • 두 위치 사이의 거리가 증가할수록 빨간색 곡선(512차원)은 비교적 안정적으로 단조감소하지만, 64차원은 그렇지 못하다.
      • 이렇게 되면, 비교적 낮은 임베딩 차원을 주로 써야 하는 시계열 모델링에는 트랜스포머가 적합하지 않을 것이다.
      • 한편 높은 임베딩 차원을 가진 모델은 파라미터 수가 늘어남에 따라 더 좋지 못한 모델이 나올 것이다.
    • 한편 임베딩 차원이 낮으면 랜덤한 두 임베딩 벡터 간의 유사도가 높아져서 두 벡터가 비교적 더 비슷해진다. (Fig 1a의 파란 곡선은 대체로 빨간색보다 위에 있다.)
      • 이렇게 되면 임베딩 공간(벡터 스페이스) 전체를 잘 활용하지 못할 것이다.
      • 논문의 Fig. 1b를 보면 시간의 길이가 30인 각 차원의 벡터로부터 첫 번째 원소와 마지막 번째 원소를 들고 왔으나, 차원이 커질수록 첫 번째 원소와 마지막 원소의 값이 같음을 알 수 있다.
      • 이러한 “anisotropic phenomenon”(논문 저자가 만든 말. 비등방적 현상)은 낮은 차원에서 임베딩을 비효율적으로 만든다. (Fig 1a의 파란 선!)

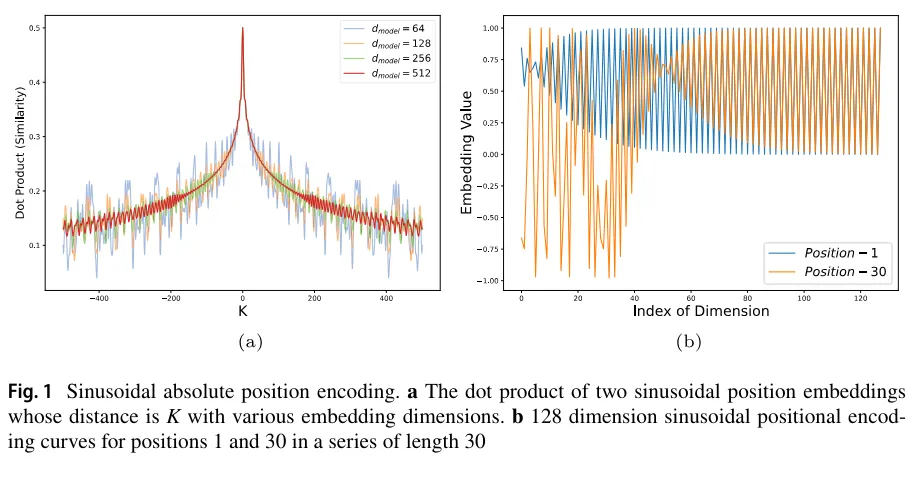
  • 그래서 우리는 distance awareness가 성립하면서도 isotropic한(”등방적”. 차원에 상관없이 임베딩 벡터 간 비슷한 정도가 동일하게끔) tAPE을 만들어야 한다.

    • distance awareness를 성립시키기 위해 위에 있던 삼각함수 임베딩을 포함시킬 것이다.

      • pi(2k)=sin(iωk), pi(2k+1)=cos(iωk), ωk=10000−2k/dmodelp_i(2k) = sin(i\omega_k), \ p_i(2k+1) = cos(i\omega_k), \ \omega_k = 10000^{-2k/d_{model}}
      • 여기서 ωk\omega_k는 삼각함수의 진동수(주기의 역수)이다.

    • series length를 L이라고 할 때, L이 커질수록 두 벡터 간의 점곱이 더 많이 진동하므로, distance awareness를 잃게 된다.

    • 위의 식에 따르면 임베딩 차원이 커질수록 (지수가 0에 가까워지므로) 임베딩 벡터가 그저 사인, 코사인 함수로부터 추출된 것이랑 별 다를 것이 없어지게 되며, 이는 anisotropic phenomenon을 야기한다.

    • 저자가 제시하는 tAPE에서는 삼각함수의 진동수에다가 임베딩 차원과 시퀀스 길이를 반영한다.

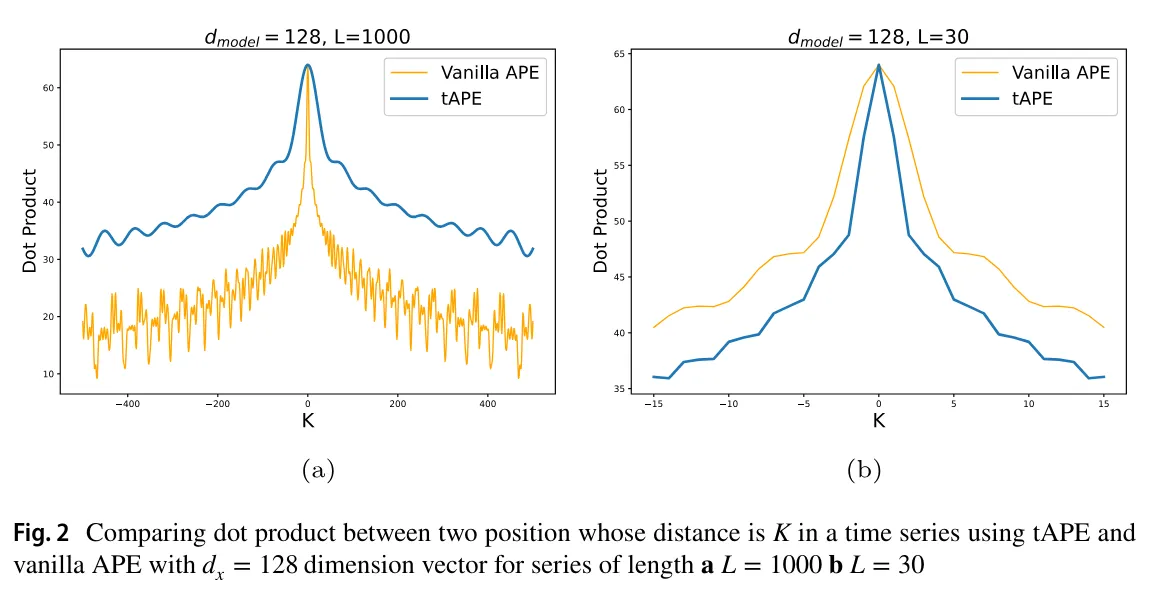
      ωknew=ωk×dmodelL\omega_k^{new} = \frac{\omega_k \times d_{model}}{L}

    • tAPE는 기존의 vanilla sinusoidal position encoding과 대비된다. Fig. 2에서 확인할 수 있다. tAPE를 씀으로써 점곱(유사도)이 조금 더 안정적으로 줄어들게 되었다.

    • 한편 Fig. 2b를 보면, 벡터 내에서 더 멀리 떨어진 원소끼리 유사도가 더 작아진 것을 볼 수 있다.

    • 한편 dmodel=Ld_{model}=L인 경우에는 기존의 APE와 똑같이 작동한다.

      • Fig. 2a는 dmodel<Ld_{model}<L인 경우, Fig. 2b는 dmodel>Ld_{model}>L인 경우를 보여준다.
      • 두 경우에서 다 distance awareness property를 유지하면서도 isotropic encoding을 보여준다.
      • tAPE가 더 좋은 점은 나중에 나올 실험 결과 섹션에 나와있다.

4.2 Efficient Relative Position Encoding (eRPE)

  • 기계 번역과 컴퓨터 비전에서 relative positional encoding에 대해 많은 확장판이 존재한다.
    • 지금까지 나온 모든 RPE는 모두 입력 임베딩에 근간을 두고 있다. (쿼리, 키, 밸류 행렬에 position matrices를 더하는 방식)
  • 구체적으로, 우리는 다음과 같은 식을 제시한다.
    αi=∑j∈L(Ai,j+wi−j)xjAi,j=exp⁡(ei,j)∑j∈Lexp⁡(ei,k)\alpha_i = \sum_{j \in L} \left(A_{i, j} +w_{i-j} \right)x_j \\ A_{i,j} = \frac{\exp(e_{i,j})}{\sum_{j \in L} \exp(e_{i,k})}
    • LL은 series length, Ai,jA_{i,j}은 어텐션 가중치, wi−jw_{i-j}는 학습 가능한 스칼라 값이며 i번째 위치와 j번째 위치 간의 상대적 위치에 대한 가중치이다. (즉, w∈RO(L)w \in \mathbb{R}^{O(L)})

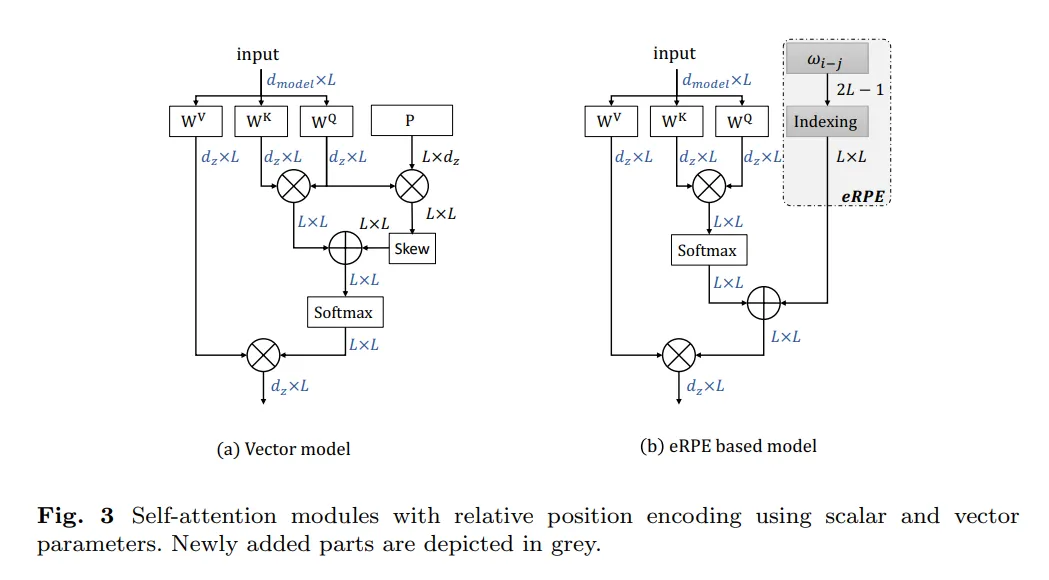
  • 시계열 데이터에서 바람직한 성질이 뭔지 알기 위해 relative position encoding과 attention의 장단점을 비교하는 것은 중요하다.
    • 첫째, relative position embedding wi−jw_{i-j}을 입력에 독립된 파라미터인 반면, 어텐션 가중치 Ai,jA_{i,j}은 입력에 따라 동적으로 바뀌는 값이다.
      • 다시 말해, 어텐션은 입력으로부터 조정되는 값이다.
      • 한편 입력에 의존하는 파라미터는 다른 time point 간의 관계에 따른 복잡한 관계를 포착하게 해준다. 시계열 데이터에서는 계절성이라고 표현하는 것이 적합할 것이다.
        • 그런데 이러한 것은 어텐션을 사용할 때 오버피팅의 위험이 더 커진다.
    • 둘째, relative position embedding wi−jw_{i-j}은 i번째 위치와 j번째 위치 간의 상대적인 간격만을 의미하며, 그 값들을 나타내는 것이 아니다.
      • 우리는 벡터보다는 스칼라 표현식인 wi−jw_{i-j}을 쓰고자 하며, 파라미터 수를 늘리지 않고 위치 차이를 나타낼 수 있게끔 한다.
      • 위와 같은 표기법의 장점은 dot-product attention function 식에다가 포함시킬 수 있기 때문이다. (위에서 봤던 식)
      • 이러한 효율적인 인코딩 방식을 eRPE라고 부를 것이다.
  • 이론적으로 어텐션 행렬에다가 상대적인 위치 정보를 통합하는 경우의 수는 많지만, 우리는 실험적으로 위의 식처럼 어텐션 행렬에 소프트맥스를 취해준 후, 상대적 위치에 대한 정보를 더해주는 것이 성능이 더 좋게 나타났다.
    • 그 이유를 추측해보면, softmax 없이도 position value들이 더 섬세해지기 때문일 것이다.
    • 더 섬세한 위치 임베딩은 시계열 태스크에서도 이점이 있는데, 그동안의 모델처럼 softmax 함수 안에다가 상대적 위치 정보를 더해주는 형식에 비해 상대적 위치에 대한 정보를 더 강조하기 때문이다.

4.2.1 Efficient Implementation: Indexing

  • 위의 식의 eRPE를 효율적으로 구현하기 위해, 우리는 사이즈 2L-1짜리 파라미터 W를 만든다.
    • 그러면 두 위치 i, j에 대응되는 파라미터 값은 Wi−j+LW_{i-j+L}이다. (파라미터는 1부터 시작한다고 가정)
    • 따라서, 우리는 2L-1 벡터에 L2L^2번 인덱싱해줘야 한다.
  • GPU에서는 gather를 이용해 인덱싱을 효율적으로 할 수 있다.
    • 인퍼런스(추론) 시에 2L-1개의 벡터로부터 L2L^2번 인덱싱하는 과정은 미리 계산해놓거나 캐싱하는 등의 방법을 이용해 속도를 키울 수 있다.
    • eRPE가 메모리 측면에서나, 속도 측면에서나 현존하는 relative position encoding 방법 중에 효율적이다.

4.3 ConvTran

  • 이제 새로운 position encoding 방법을 이용해 새로운 시계열 분류 신경망을 만드는데 쓸 수 있는지 볼 차례이다.
  • 입력의 길이를 줄이기 위해 컨볼루션 연산을 이용하여 입력의 길이가 다루기 쉬워지도록 바꾼다.
    • 앞서 논의한 바에 따르면, 어텐션 전체를 계산하는 데에 입력 길이의 제곱에 비례하는 시간 복잡도를 가지고 있다.
    • 그래서 아까 소개한 방법을 그대로 어텐션에 적용하면 속도가 매우 느릴 것이다.
    • 컨볼루션을 다루면 지역적 특징을 잡기 아주 좋다. 그래서 raw time series에 있는 지역적 특징을 잡아낼 수 있다.
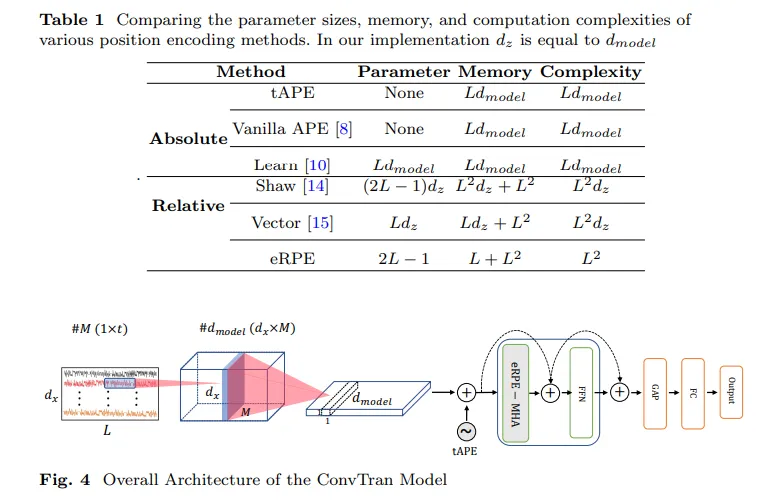
  • Fig. 4에 나와있듯이, 첫 단계의 컨볼루션층에는 M개의 시간 필터(temporal filter)가 input data에 적용된다.
    • 이 단계에서는 모델이 입력으로부터 지역적 특징을 뽑아낸다.
  • 다음 단계에서는, temporal filtering의 출력들이 dx×Md_x \times M 형태의 필터와 컨볼루션 연산이 이뤄진다.
    • 이 단계에서 다변량 시계열 데이터 내의 변수 간의 상관관계가 포착된다.
    • 그래서 인풋의 채널이 늘어났다가 크기가 줄어든다.
    • 이런 선택을 한 가장 중요한 이유는 트랜스포머 구조의 피드포워드 신경망(FFN) 역시 input size를 늘렸다가 나중에 정사영을 통해 차원을 원래대로 줄이기 때문이다.
  • 입력 임베딩을 트랜스포머 블록에 넣기 전에 tAPE가 생성한 position embedding을 이용한다.
    • 이것이 있어야 트랜스포머 블록이 시간적 순서를 포착할 수 있다.
    • 위치 임베딩 벡터의 차원은 dmodeld_{model}이고, 입력 임베딩의 차원과 똑같다.
    • 멀티 헤드 어텐션 안에는, L×dmodelL \times d_{model}차원의 입력이 먼저 선형 층으로 L×dz×3L \times d_z \times 3차원으로 변하여 qkv 행렬을 얻기 위한 준비를 한다.
    • 여기서 dzd_z는 모델의 차원을 나타내며, 사용자에 의해 정의되는 값이다.
  • 각 L×dzL \times d_z 행렬은 쿼리(q), 키(k), 밸류(v)를 나타낸다.
    • 이러한 q, k, v 행렬은 각각 h×L×dz/hh \times L \times d_z/h 차원으로 reshape되어서 각 h개의 어텐션 헤드를 나타낸다.
    • 각 어텐션 헤드는 시계열에서 다른 패턴을 포착하는 데에 중요하다.
      • 예를 들어, 한 개의 어텐션 헤드는 노이즈를 제외한 데이터에 집중할 수 있고, 다른 어텐션 헤드는 계절성과 같은 트렌드에 집중할 수 있다.
    • 그래서 q, k, v 행렬이 있으면, 위의 식대로 멀티 헤드 어텐션 블록 안에서 어텐션 연산을 수행할 수 있다.
  • 동시에, 위의 식에 따르면 L×LL \times L shape의 eRPE가 어텐션 블록의 출력에 더해진다.
    • 우리는 파라미터 수를 늘리지 않고도 콘볼루션 커널을 만들기 위해 wi−jw_{i-j}이라는 노테이션을 생각한다.
    • relative position embedding은 모델로 하여금 시간 순서를 학습시킬 수 있을 뿐 아니라 한 쌍의 time points까지 학습시킬 수 있다.
    • 이렇게 하면 다른 임베딩 전략보다 더 풍부한 정보를 포착할 수 있다.
  • FFN은 두 개의 선형 층과 GELU(Gaussian Error Linear Units)을 활성화 함수로 갖는 다층 퍼셉트론층이다.
    • skip connection을 통해 FFN의 출력에 입력 값이 다시 더해진다.
    • 마지막으로 global average pooling을 거쳐 fully-connected layer에 들어가서 ELU 활성화 함수를 거쳐 최종 결과값을 얻는다.

5 Experimental Results

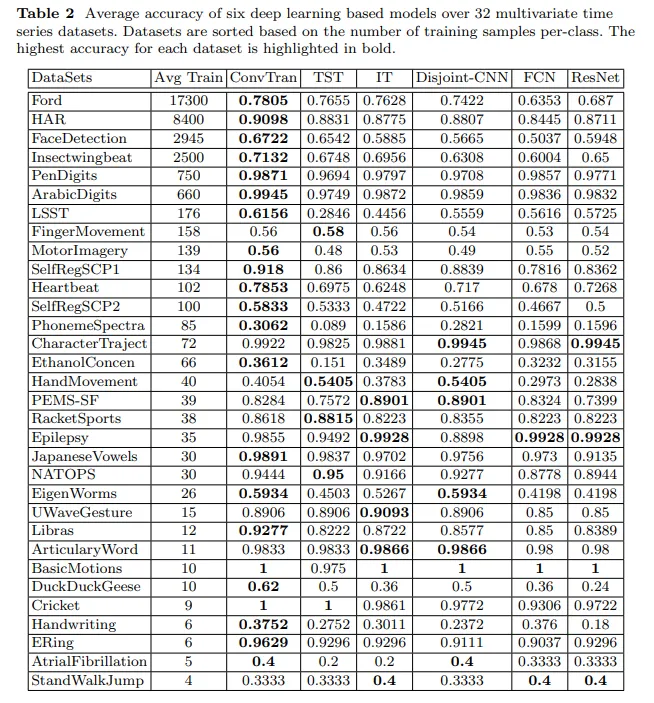
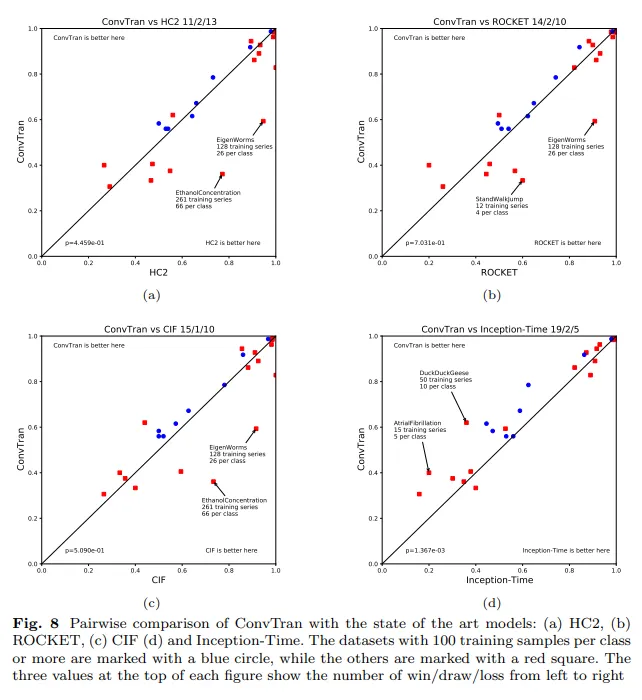
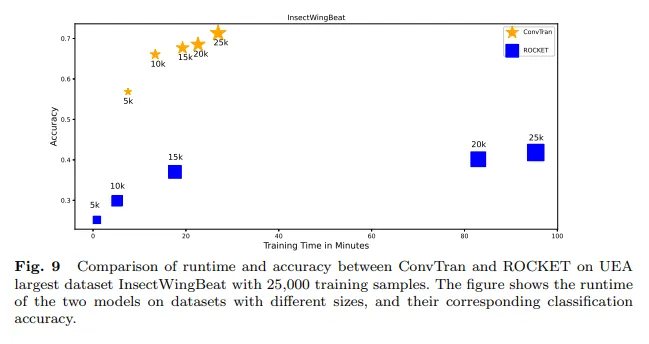
시간 분량 상 넘어갑니다. ConvTran 모델을 평가하는 내용이고, 많은 데이터셋에서 state-of-the-art를 달성했다는 내용이 담긴 챕터입니다.

6 Conclusion

  • 이 논문에서는 시계열에서의 position encoding의 중요성에 대해 처음 연구하였다.
    • 현재 존재하는 position encoding의 한계에 기반하여, tAPE와 eRPE라는 방법을 소개하였다.
    • 이 방법을 트랜스포머 블록에 통합시켜서, 다변량 시계열 분류 작업을 위한 딥러닝 프레임워크를 소개하였다.
    • 많은 실험에서 ConvTran 모델이 우위를 점했으며, 다변량 시계열 분류에서 state-of-the-art를 달성하였다.
    • 앞으로는, 이 논문에서 소개한 새로운 트랜스포머 블록의 효과를 다른 트랜스포머 기반 시계열 분류 모델과 anomaly detection과 같은 다운스트림 태스크에 적용하여 그 성능을 평가할 예정이다.
profile
cacbon_dioxit

0개의 댓글