[BOJ 1931] 회의실배정

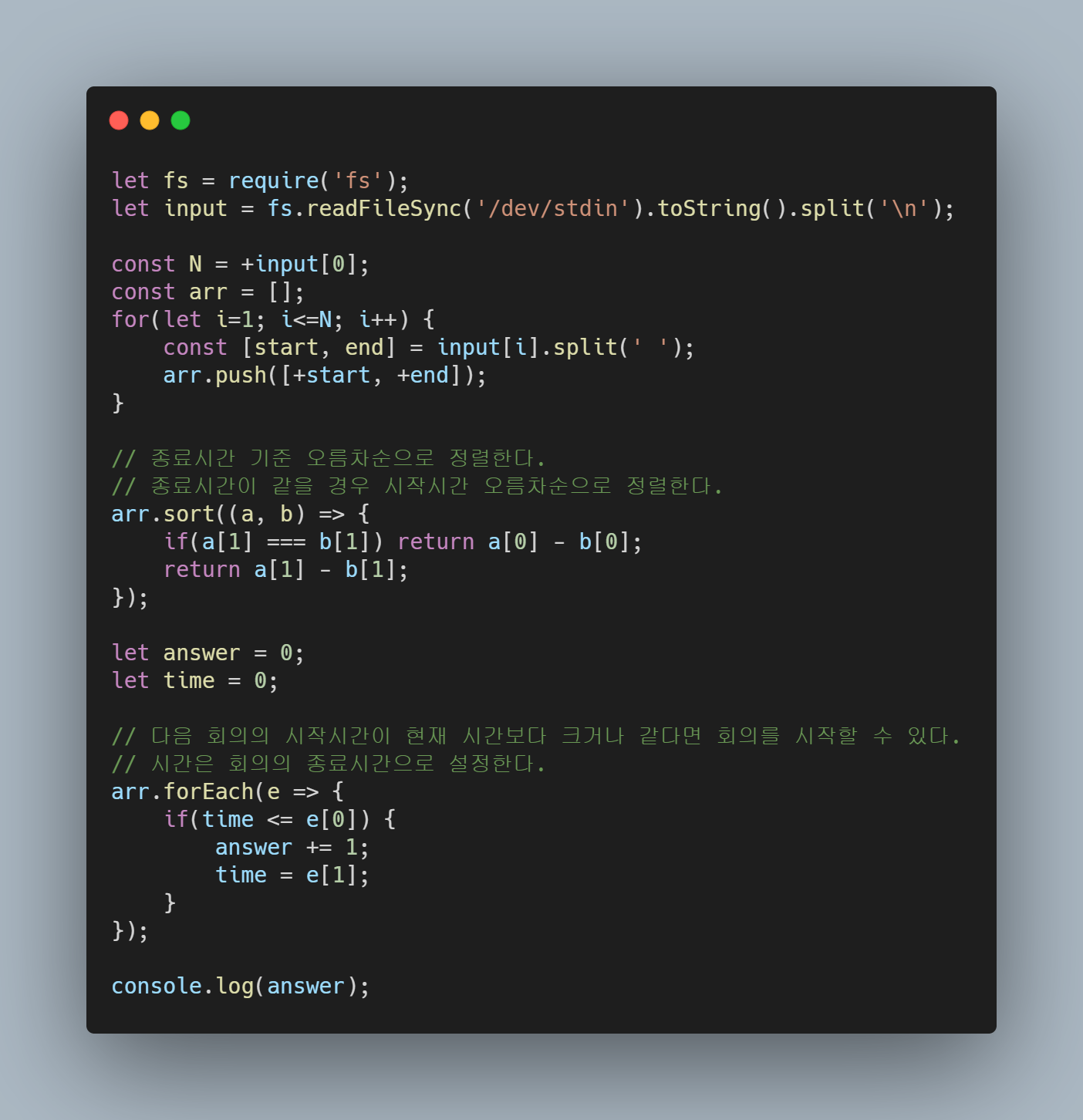
이 문제는 이곳에서 확인할 수 있습니다.

이 문제는 주어지는 회의 시작시간과 종료시간을 바탕으로 회의실을 사용할 수 있는 최대 회의의 개수를 구하는 문제입니다.

전형적인 그리디 알고리즘 문제로서 반례가 없이 배열을 순회할 수 있도록 배열을 재구성해야 합니다. 보통 다음과 같은 아이디어를 내볼 수 있습니다.

1. 시작시간이 빠른 순서대로 정렬한다.
   
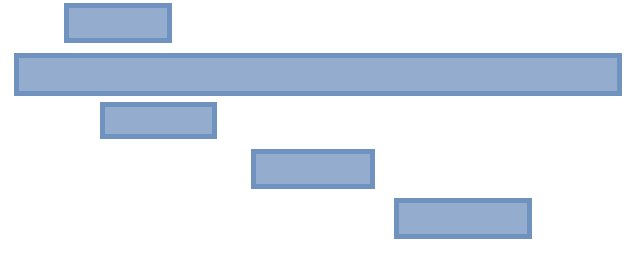
   이 경우에는 긴 시작시간이 빠르고 회의시간이 긴 회의가 회의실에 배정되어 다른 회의는 배정될 수 없게 됩니다.

2. 회의시간이 짧은 순서대로 정렬한다.
   
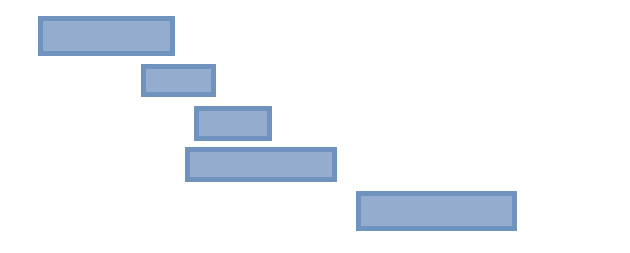
   이 경우에는 여러 회의 시간 중 중간에 짧은 회의가 있을 경우, 이 회의가 가장 먼저 배정되면 이 회의로 인해 앞뒤의 다른 회의가 배정될 수 없게 됩니다.

3. 종료시간이 빠른 순서대로 정렬한다.
   이 경우에는 반례 없이 문제의 답을 찾을 수 있습니다.
   회의를 시작하기 위해서는 회의실에서 회의가 진행 중이지 않아야 하고, 회의가 진행 중이지 않기 위해서는 현재 시간이 종료 시간보다 뒤에 있어야하기 때문입니다.
   즉, 회의실이 비어있는 시간을 순서대로 찾아내는 것이 핵심입니다.
   
   종료 시간이 같을 경우, 시작 시간이 빨라야 회의실에 더 일찍 들어가 회의를 시작할 수 있으므로 시작 시간 오름차순으로 정렬해야 합니다.

그리디 알고리즘 특성 상 여러 케이스를 모두 확인해야하는 번거로움이 있습니다.
그럼에도 불구하고 가장 적절한 케이스를 찾았을 때 코딩을 하는 것은 아주 간단합니다.